Ряд Фурье для периодических сигналов

Для детерминированных сигналов наибольшее распространение получили методы спектрального анализа, использующие преобразования Фурье. В роли базиса С_к (t) могут использоваться как гармонические функции, так и экспоненциальные, а роль коэффициентов а_k играют амплитуды гармоник. Доказано, что сложный детерминированный сигнал X (t) на ин­тервале (t₂— t₁) можно заменить суммой т взаимно ортогональных на этом интервале сигналов С_k (t), причем погрешность такой аппроксима­ции будет зависеть от числа членов ряда т.

Для описания периодических сигналов наиболее часто используют ортогональную систему тригонометрических функций {cos kω₀t и sin kω₀t}. Описание сигналов тригонометрическими функциями называют обычным или обобщенным рядом Фурье. В этом случае любой периодический сигнал X(t) можно представить на интервале 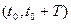рядом элементарных сигналов:

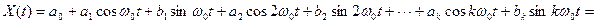
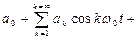
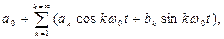(1.12)

где a ₀ – постоянная составляющая (среднее значение) сигнала; a _k и b _k – амплитуды соответственно косинусной и синусной составляющих k – гармоники основной частоты.

Коэффициенты ряда Фурье определяются по формулам

,

,

,

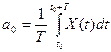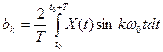Если объединить косинусные и синусные составляющие, то (1.12) можно представить в виде

, (1.13)

где A _k – амплитуда k - ой гармоники, 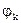- фаза k-й гармоники;

Смысл выражения (1.13) состоит в том, что периодическая функция X (t) может быть представлена суммой косинусоидальных колебаний с частотами, кратными основной частоте ω₀ и с определенным образом подобранными амплитудами A_k и начальными фазами 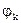. Совокупность величин A_k называется спектром амплитуд; совокупность величин 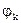– спектром фаз.

Разложив косинус суммы в выражении (1.13), получим

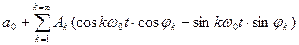, (1.14)

Откуда находим

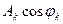b _k =-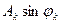

, ,

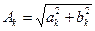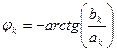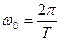
Периодический сигнал X(t) можно также представить суммой комплексных экспоненциальных сигналов - с помощью экспоненциального ряда Фурье. Экспоненциальный ряд Фурье для периодической функции является второй формой ряда Фурье.

Комплексную форму ряда Фурье получают на основании формулы Эйлера

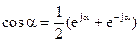
Приняв 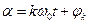и введя обозначения:

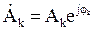- комплексная амплитуда k-й гармоники (содержит информацию о фазе и амплитуде); 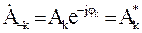- комплексно-сопряженная амплитуда. Представим ряд (1.13) в комплексной форме

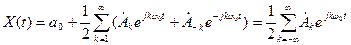. (1.15)

Коэффициенты ряда (1.15) вычисляются по формуле

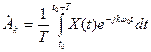(1.16)

Суммы, определяемые выражениями (1.13) и (1.15) будут тождественны при выполнении условий 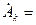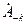, φ_-k = φ_k, φ₀ = 0. При этом модуль комплексной амплитуды будет равен амплитуде соответствующей гармонической составляющей, а аргумент равен начальной фазе составляющей.

Дискретный спектр периодического сигнала, определяемый с помощью специальных средств измерения (анализаторов гармоник) характеризуется совокупностью важных информативных параметров сигнала x(t) – значениями амплитуд и фаз отдельных гармоник, полосой частот и др.

Результат представления периодического сигнала рядом Фурье:

§ спектр сигналов дискретный;

§ расстояние между спектральными линиями кратно основной частоте;

§ амплитудный спектр – четная функция частоты:

§ фазовый спектр – нечетная функция частоты

§ амплитуда спектральных коэффициентов тригонометрического ряда Фурье совпадает с амплитудой гармоник сигнала;

§ амплитуда спектральных коэффициентов комплексного ряда Фурье вдвое короче, кроме постоянной составляющей, спектр сигнала двусторонний;

Периодический импульсный сигнал X(t) с периодом повторения Т согласно (1.12) можно представить состоящим из периодических синусоидальных сигналов с частотами 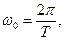2w₀, 3w₀, …,kw₀ и амплитудами A₀, A₁, A₂, A₃, … A_k. Периодический сигнал X(t) обладает дискретным (линейчатым) спектром и графически изображающимся в виде вертикальных (спектральных) линий вдоль оси частот в точках w₀, 2w₀, 3w₀ и т. д. Высота каждой из этих спектральных линий пропорциональна амплитуде данной частотной составляющей. В общем случае сумма (1.12) представляет бесконечный ряд, но на практике пренебрегают очень малыми значениями амплитуд, т.е. спектр сигнала искусственно ограничивают. Частотные составляющие спектра являются комплексными числами, и поэтому для представления сложной периодической функции необходимо иметь два дискретных спектра: спектр амплитуд (рис.1.7,а) и спектр фаз (рис. 1.7,б). Спектром фаз называют совокупность начальных фаз и соответствующих частот гармоник. Спектр амплитуд и спектр фаз однозначно определяют сигнал. Часто на практике ограничиваются рассмотрением только спектра амплитуд.

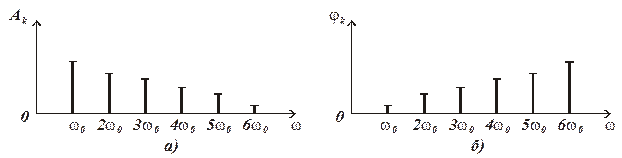Рис. 1.7. Спектральное представление сложной периодической функции: а) спектр амплитуд, б) спектр фаз

Важно:

1. Спектры периодических сигналов самой различной формы, но с одинаковым периодом T содержат одни и те же гармонические составляющие (основную и кратные ей высшие гармоники), однако амплитуды их различны для различных сигналов;

2. Если построить аналогичные спектры модулей комплексных амплитуд 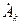ряда Фурье в комплексной форме, то все спектральные линии будут вдвое короче ( 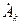= А_k/2), кроме линии, изображающей постоянную составляющую; спектр будет двусторонний, т.е. спектральные линии расположены симметрично влево и вправо относительно оси ординат A_k. Физическое представление отрицательных частот - математическая абстракция. Область отрицательных частот надо учитывать, чтобы избежать ошибок при спектральном представлении сигналов.

Так как для периодических сигналов спектр неограничен, то для передачи такого сигнала по измерительному каналу, последний должен иметь бесконечно большую полосу пропускания. Практически же все каналы связи имеют ограниченную полосу пропускания, и поэтому форма сигналов при передаче по каналу изменяется даже при отсутствии в этой полосе амплитудных и фазовых искажений. В идеальном случае для передачи сигнала без искажения необходимо передавать всё бесконечное число гармоник. На практике, при передаче сигнала, его спектр ограничивают, пропуская через канал связи наиболее существенную часть спектра. В связи с этим введено понятие практической ширины спектра сигнала, под которой понимают диапазон частот, в пределах которого находится наиболее существенная часть спектра сигнала. Выбор практической ширины спектра сигнала определяется по двум критериям: энергетическому и критерию допустимых искажений формы сигнала. С энергетической точки зрения практическая ширина спектра периодического сигнала определяется как область частот, в пределах которой сосредоточена основная часть мощности сигнала и зависит от длительности импульса t.

Например, для периодической последовательности однополярных прямоугольных импульсов длительностью t и скважностью, равной двум, ряд Фурье имеет вид:

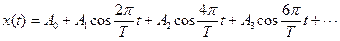, (1.17)

где

.

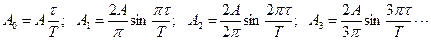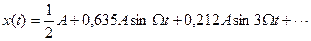
Спектр такого сигнала состоит из постоянной составляющей и большого числа гармоник, амплитуды которых А₁, А₂, А₃ и т.д. постепенно уменьшаются с увеличением частоты. Для примера, зададимся исходными параметрами периодической последовательности импульсов: амплитуда импульсов равна 1 В, длительность импульсов τ = 20 мс, скважность Q = T/τ = 6. Подставив исходные данные в (1.17) получим значения амплитуд гармоник, входящих в первый лепесток спектра: A₀ = 0,16В, A₁ = 0,31В, A₂ =0,27В, A₃ = 0,21В, A₄ =0,16В, A₅ = 0.1В. Амплитуда шестой гармоники A₆ =0В (аргумент синуса равен π). Далее амплитуды гармоник начнут возрастать, а амплитуда 12 гармоники опять обратится в ноль. Частота первой гармоники всегда равна частоте следования импульсов – f₁ = 1/(120*10^-3) = 8,33 Гц, f₂ = 16,6 Гц, f₃ = 24,9 Гц, f₄ = 33,2 Гц, f₅ = 47,5 Гц, f₆ = 50 Гц. Частоты гармоник, амплитуды которых обращаются в ноль, кратны величине обратной длительности импульса: 1/τ, 2/τ, 3/τ, 4/τ и т.д.

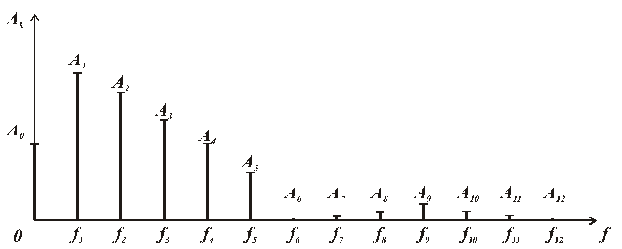
Рис. 1.8. Спектр амплитуд последовательности однополярных импульсов

Если для передачи этой серии импульсов выделяется полоса частот, равная DF_с =1/τ =1/20*10^-3 = 50 Гц, то передача будет осуществляться в нашем случае пятью гармониками (от f ₁ = 8,3 Гц до f ₅ = 41,67 Гц). Увеличим частоту следования импульсов втрое, то уравнение (1.17) будет иметь вид

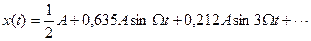
Амплитуды постоянной составляющей и первой гармоники увеличились (первый лепесток спектра содержит всего одну гармонику), амплитуда второй гармоники равна нулю (f₂ = 1/τ = 50 Гц). Если передача будет происходить по-прежнему в полосе DF=1/τ = 50 Гц, то будут переданы только постоянная составляющая и первая гармоника. Однако, несмотря на разное количество передаваемых гармоник, воспроизведение формы импульса в обоих случаях будет почти одинаковым. Воспроизведение формы импульса зависит только от полосы частот DF, которая определяется его длительностью τ. Практически ширина спектра последовательности прямоугольных импульсов выбирается из соотношения:

DF = μ/ τ. (1.18)

При μ = 1 обеспечивается передача основной части энергии сигнала, которая складывается из суммы энергии постоянной составляющей и всех гармоник. В полосе частот DF= 1/ τ сосредоточено более 90% всей энергии сигнала, достаточно точно передается амплитуда импульсов и данный диапазон частот может быть принят в качестве практической ширины спектра одиночного прямоугольного импульса.

Хуже для некоторых сигналов (треугольный, экспоненциальный, трапецеидальный) передается их форма. На практике μ берется в пределах (1…2). Увеличение μ приводит не только к более точному воспроизведению формы импульса, но и к значительному расширению полосы частот, что обычно не рационально. Иногда в целях экономии полосы частот, а также, если форма импульса не важна, выбирают μ = ½.

Важным условием передачи сообщений по каналу без искажения является выполнение требования DF_c £ F_канала, т.е. полоса частот, занимаемая полезным сигналом, не должна превышать диапазона частот канала.

Передача всех значений сигнала x(t) является не обязательной, если у него ограниченный спектр. Согласно т еореме равномерных отсчетов сигнал с ограниченным спектром, не имеющий спектральных составляющих с частотами выше ¦_m, однозначно определяется своим мгновенными значениям (отсчетами), разделенными одинаковыми интервалами времени, равными или меньше 1/2¦_m

Отсчеты функции осуществляются через интервал (∆t< 1/2¦_m) или с частотой, большей или равной 2¦_m отсчетов в секунду. Частота отсчетов должна быть в два раза больше высшей частоты ¦_m, имеющейся в спектре сигнала, т.е. на каждый период наивысшей частотной составляющей сигнала должно приходиться, по крайней мере, по два отсчета. Информация о непрерывном сигнале полностью определяется 2¦_m отсчетами в секунду. Количество информации зависит от того, сколько различных уровней или значений могут принимать отсчеты.

Если подходить к выбору практической ширины спектра сигнала по критерию допустимых искажений формы сигнала, то достаточно точно будет воспроизведена форма прямоугольного сигнала уже при пятой гармонике сигнала, т.е. k=5 в выражении (1.17).

Дата добавления: 2017-01-14