Интеграл Фурье для непериодических сигналов 2 страница

и _ФМ(t) = u ₀ cos (w ₀ t + K_Ф sin W t), (2.12)

где K_Ф= - индекс фазовой модуляции, ∆φ - максимальный сдвиг по фазе (девиация фазы).

Аналитическая запись и структура спектра при ФМ сигнала при гармонической модуляции полностью совпадает со спектром ЧМ сигнала. Индекс фазовой модуляции K_Ф зависит от девиации фазы ∆φ. Однако ЧМ и ФМ сигналы существенно различаются при изменении частоты модуляции и амплитуды модулирующего сигнала. При ЧМ девиация частоты пропорциональна амплитуде модулирующего сигнала и не зависит от частоты модуляции. При ФМ девиация фазы пропорциональна амплитуде модулирующего сигнала и зависит от частоты. Как следствие этого, девиация частоты при ФМ линейно увеличивается с ростом частоты. Полоса частот занимаемая таким сигналом будет равна

D F_ФМ = 2 W _n (K_Ф + 1).

При K_Ф >> 1 спектр частот при ФМ похож на спектр ЧМ. При K_Ф << 1 спектр частот D F_ФМ = D F_АМ = 2 W _n. Фазовая модуляция аналогична частотной, и отличаются они друг от друга лишь методами их осуществления.

Двукратные виды модуляции. Они обладают рядом достоинств, в том числе позволяют повысить помехоустойчивость передачи сообщения. При модуляции типа АМ – ЧМ сначала сообщением модулируется по амплитуде первый переносчик, который называется в данном случае поднесущей. Далее амплитудно-модулированный сигнал модулирует второй переносчик, или несущую, в результате чего имеем сигнал, модулированный по частоте. Иногда применяется модуляция ЧМ – АМ, при которой помехоустойчивость обеспечивается ЧМ, а экономия полосы частот АМ. При этом поднесущая модулируется по частоте, а затем частотно-модулированный сигнал модулирует несущую по амплитуде. По такому же принципу осуществляется модуляция типа ЧМ – ЧМ. На рис. 2.5 приведен пример двукратной модуляции типа АМ-ЧМ.

Амплитудная манипуляция. Амплитудная манипуляция происходит по тем же схемам, что и амплитудная модуляция, только вместо несущего гармонического колебания на модулятор подается последовательность импульсного сигнала. Спектр частот при амплитудной манипуляции, так же как и при АМ, содержит три составляющие: несущую частоту, верхнюю и нижнюю боковые полосы частот. В зависимости от коэффициента m различают два варианта амплитудной манипуляции: m<1 и m=1. На рис. 2.6 показаны различные варианты манипуляций: амплитудная, частотная и фазовая. Амплитудная манипуляция широко применяется при передаче телеграфных сигналов. В случае m<1 на рис. 2.6,б) показана последовательность импульсов, получающихся на выходе модулятора, выполненного на транзисторе, работающем в ключевом режиме. При m=1 на рис. 2.6,в) показаны искажение формы импульсов при передаче их по реальному каналу, обладающему ограниченной полосой пропускания. На рис. 2.6,г) и 2.6,д) показан принцип образования частотной и фазовой манипуляции. Амплитуда составляющих зависит от m. Полоса частот определяется как D F = 2 μ/τ.

Рис. 2.5. Двукратная модуляция типа АМ-ЧМ

Рис. 2.6. Амплитудная манипуляция

2.3. Импульсные модулированные сигналы

Последовательность прямоугольных импульсов описывается рядом Фурье (1.15)

и характеризуется рядом информативных параметров: амплитудой, частотой, длительностью импульсов, которые входят в это выражение для гармоник A_k. Используя серию импульсов в качестве переносчика и, изменяя любой из этих параметров под воздействием сообщения, мы тем самым осуществляем импульсную модуляцию.

При амплитудно-импульсной модуляции (АИМ) у переносчика в виде последовательности импульсов изменяют только амплитуду по закону модулирующего сигнала е(t). Рассматривая простейший случай, когда модулирующий сигнал e(t) является синусоидальным (2.2)

e(t) =E cos W t

Изменение амплитуды при АИМ происходит по закону

U_АИМ = U₀ + K e(t),

тогда АИМ сигнал представим в виде:

. (2.13)

Подставляя выражение e(t) в (2.13)получим:

U _АИМ(t) = . (2.14)

Спектр такого сигнала бесконечен по частоте. В этом случае при определении требований к полосе пропускания измерительного канала надо исходить из допустимой погрешности искажения сигнала за счет ограничения его частотного диапазона. Из выражения (2.14) следует, что при модуляции кроме основных спектральных линий, содержащихся в спектре сигнала (первое слагаемое), дающее спектральные линии на частотах ω₀, 2 ω₀, 3 ω₀, 4 ω₀ = 2π/τ, 5 ω₀, 6 ω₀, 7 ω₀, 8 ω₀ = 4π/τ и т.д. появляются дополнительные линии меньших размеров, расположенные на частотах kω₀ ± Ω по обе стороны от каждой спектральной линии переносчика на расстоянии ± Ω (рис. 2.7).

Рис. 2.7. Спектр амплитуд при амплитудно-импульсной модуляции

При более сложной модулирующей функции e(t) по обе стороны от спектральных линий переносчика появляются боковые полосы дополнительных спектральных составляющих, число которых определяется полосой частот модулирующей функции. Строение этих полос зависит от вида модуляции.

Частотно-импульсная модуляция (ЧИМ) заключается в изменении частоты следования импульсов пропорционально амплитуде модулирующего сигнала. Ширина полосы частот определяется длительностью импульса.

В случае фазо-импульсной модуляции (ФИМ) смещается положение импульсов относительно тактовых точек в соответствии с изменением модулирующего сигнала (см. рис. 2.6,и). Импульс сдвигается вправо и влево на ±∆t при соответственно увеличении и уменьшении мгновенного значения сигнала e(t).

Широтно-импульсная модуляция (ШИМ) заключается в изменении длительности импульсов переносчика в соответствии с законом изменения модулирующего сигнала e(t) (см. рис. 2.1,к). Изменение ширины импульсов осуществляется за счет изменения положения заднего фронта импульса переносчика.

При время-импульсной и частотно-импульсной модуляции даже при простейшей синусоидальной модулирующей функции e(t) (2.3), спектр которой представляется одной гармоникой, вокруг каждой боковой спектральной линии располагается бесконечно большое число дополнительных гармоник носителя, которые быстро убывают.

Важно, что независимо от вида модуляции, ширина спектра сигнала определяется его τ, т.е. определяется шириной (длительностью) импульса и может быть оценена величиной (2.10)

∆F = μ/ τ,

где μ – постоянная, зависящая от формы импульса и имеющая порядок единицы.

Детектирование импульсных модулированных сигналов выполняется при помощи фильтров низких частот в случае, если смещенные спектры, образованные вокруг спектральных гармоник несущего сигнала не перекрываются. ФНЧ должен иметь частоту среза больше ширины спектра сообщения. При перекрытии смещенных спектров задача фильтрации сигнала усложняется.

Кодо-импульсная модуляция (КИМ) является особым видом модуляции, при которой имеет место цифровое измерение мгновенных значений сигнала x(t), в определенные моменты времени и представление результата в виде кодового сигнала, удобного для передачи по каналу связи. Применение КИМ при одном канале связи требует больших затрат времени, т.к. каждое мгновенное значение сигнала x(t) передается несколькими импульсами, но повышает помехозащищенность в соответствии с свойствами выбранного кода. Строго говоря, это уже кодирование сигнала, но термин КИМ получил широкое распространение.

Многократные методы модуляции. Сообщение может быть передано сложным сигналом, образованным несколькими поочередными модуляциями, что позволяет повысить их помехоустойчивость передачи. Это может быть двойная и тройная модуляция. При двойной модуляции сообщение модулирует импульсную поднесущую, которая превращаясь в сигнал, модулирует в свою очередь высокочастотную несущую, например АИМ-АМ, ШИМ-АМ, АИМ-ЧМ, ШИМ-ЧМ. При тройных модуляциях первая модуляция импульсная, а вторая и третья непрерывные, например АИМ-АМ-ЧМ, ШИМ-АМ-ЧМ и т.д.

2.4. Цифровые методы модуляции

Цифровую модуляцию используют для передачи непрерывных сообщений дискретными методами. Ее сущность заключается в том, что непрерывный сигнал, квантованный по своим значениям и дискретный по аргументу, рассматривается в определенной системе счисления в виде чисел, которые затем кодируются для преобразования их в кодовые комбинации электрических сигналов. Полученной последовательностью кодовых видеосигналов аналоговым или дискретным способом модулируют высокочастотный сигнал переносчика. Наиболее распространенными цифровыми видами модуляции являются импульсно-кодовая модуляция (ИКМ), дельта-модуляция (ДМ) и комбинированные виды (ИКМ-ДМ).

Достоинством систем с цифровым способом передачи сигналов: высокая помехоустойчивость, низкая чувствительность к нелинейным искажениям, возможность восстановления сигналов в узлах сетей связи, универсальная форма представления сигналов для различных сообщений (речь, телевизионные изображения, дискретные данные, команды управления работой устройств связи и т. п.), достаточно простое согласование этих систем с различного рода ЭВМ и т д.

Недостаток этих систем: расширение занимаемой полосы частот, необходимость обеспечения точной синхронизации сигналов и построения специальной аппаратуры для регенерации сигналов на линиях большой протяженности.

Наметились следующие основные области применения цифровых методов модуляции: разделение действующих соединительных линий между АТС, построение интегральных сетей связи с электронными АТС, радиорелейные линии связи прямой видимости и дальние линии связи, спутниковые системы с многостанционным доступом, волноводные и оптические линии многоканальной связи, телеметрия.

Наибольшее развитие получили системы с ИКМ для разделения телефонных и спутниковых линий связи.

2.5. Контрольные вопросы

1. Дайте определение понятию модуляция.

2. В чем принципиальное отличие модулирующего сигнала от переносчика?

3. Запишите выражение для АМ сигнала для случая двух синусоидальных сигналов.

4. Как выглядит спектр АМ сигнала для случая двух синусоидальных сигналов?

5. Как изменится спектр АМ сигнала, если модулирующий сигнал периодический сложной формы, а переносчик высокочастотный синусоидальный сигнал?

6. Как рассчитать полосу частот АМ сигнала?

7. В чем сущность балансной модуляции?

8. Как выглядит спектр сигнала при ЧМ и ФМ?

9. Что такое амплитудная манипуляция?

10. В чем отличие спектра АМ сигнала от спектра сигнала АИМ?

11. Как выполняется цифровая модуляция?

12. Где используется цифровая модуляция?

3. Преобразование сигналов линейными и нелинейными цепями

Сигналы измерительной информации преобразуются в различ­ных физических цепях измерительного канала. Характер преобразования определяется свойствами этих цепей, описы­ваемыми соответствующими функциями преобразования, которые мо­гут символизировать любую математическую операцию: интегри­рование, дифференцирование, умножение и т. д. Физические цепи в зависимости от свойств их параметров подразделяются на линейные и нелинейные. Линейными считаются цепи, параметры которых не зависят от параметров проходящих через них сигналов (токов и напряжений). Нелинейными считаются цепи, параметры которых зависят от проходящих через них сигналов. Причиной нелинейности системы (цепи) является наличие в ней инерционных элементов (катушек индуктивности, конденсаторов, инерционных устройств и др).

Связь между выходным Y (t) и входным X (t)сигналами цепи описывается уравнением (функцией преобразования):

Y(t)=F[X(t)], (3.1)

где F — символ функции.

Свойство линейности идеальной стационарной системы предполагает выполнение двух принципов – принципа аддитивности и принципа гомогенности (однородности). Принципы эти очень сильно связаны между собой. Под аддитивностью понимается суперпозиция причин и результатов. Система аддитивна тогда, когда для любой пары функций времени (t) и (t)(входящих в пространство входных функций этой системы) ее реакция на сумму [ (t)+ (t)]есть сумма ее реакций отдельно на (t) и (t).

F[ (t)+ (t)]=F[ (t)]+F[ (t)]; (3.2)

Под однородностью понимается наличие пропорциональности между входным и выходным сигналами. Для всех входных сигналов X(t) (в пространстве входных сигналов этой системы), для всех вещественных постоянных k реакция системы на входной сигнал [ kX(t)] в k раз больше реакции системы на входной сигнал X(t).

F[kX(t)] = kF[X(t)], (3.3)

где k = const.

Важным свойством аддитивности является ее отношение к гомогенности. Это отношение заключено в следующем утверждении: если какая-либо идеальная система аддитивна, тогда для всех практических случаев она также и гомогенна, что говорит о детерминированности идеальной стационарной системы.

Рассмотренная идеальная модель стационарной линейной системы в силу своей простоты и наглядности используется для создания фундаментальных основ теории систем. Степень отличия реальной линейной стационарной системы от идеальной, зависит от величины вносимых ею искажений в передаваемый сигнал, которые условно делят на линейные, нелинейные и шумовые. Линейные искажения обусловлены неравномерностью частотных характеристик и нелинейностью фазовых характеристик реальной линейной системы. Нелинейные искажения возникают из-за наличия локальных отклонений статической характеристики или функции преобразования системы от линейной. Подобные локальные отклонения характеристики системы от линейной зависимости для конкретной системы являются строго индивидуальными и определяются конструктивными особенностями или “дефектами”. Поэтому, когда говорят о реальной линейной системе, то имеют в виду линейность ее номинальной (идеальной) характеристики или функции преобразования. Наконец, под шумовыми искажениями выходного сигнала понимают флуктуации, возникающие в системе либо по причине того, что они присущи самой системе, либо под воздействием внешних влияющих факторов. Например, для электронных систем, подобные внутренние флуктуации зарождаются, в результате случайного поведения носителей заряда внутри электронных составляющих системы и как реакция системы на изменения внешних влияющих факторов.

Примером реальных линейных систем могут служить информационные системы, различного рода линейные преобразователи информативного параметра сигнала, перестраиваемые генераторы, линейные средства измерений. Например, в случае перестраиваемых генераторов за входную величину можно принять номинальное значение задаваемого информативного параметра сигнала генератора, а в качестве выходной величины – фактическое значение информативного параметра генерируемого сигнала.

Важным является то, что физические причины возникновения искажений при передаче, генерации и измерении сигналов для всех рассматриваемых классов линейных систем и цепей, их составляющих, являются общими. Одинаковыми являются последствия искажений в системах и цепях, которые приводят к отклонениям информативных параметров выходных сигналов от результатов требуемых преобразований информативных параметров входных сигналов, т.е. к появлению погрешности преобразования.

Известно, что погрешность преобразования линейной системы, не связанная с ее инерционностью, а обусловленная существующими в ней искажениями и флуктуациями, в основном может быть представлена двумя составляющими:

1) Основной погрешностью системы, определяемой отличием мгновенной характеристики преобразования системы в нормальных условиях эксплуатации от индивидуальной характеристики преобразования (основная погрешность является статической или квазистатической);

2) Дополнительной погрешностью, определяемой чувствительностью системы к внешним влияющим факторам (в ГОСТ 8.009–84 для средств измерений дополнительная погрешность названа функцией влияния).

Так как основная и дополнительная погрешности не связаны с инерционными свойствами, их можно объединить в одну, статическую погрешность, определяемую отличием реальной функции преобразования системы от номинальной.

Практические исследования показали, что мгновенной функции преобразования линейных систем присущи свойства нестационарной случайной функции y = f (x, t) информативного параметра X.

Существуют два метода анализа стационарных линейных систем - метод интеграла наложения (Дюамеля) и спектральный, основанный на использовании преобразований Фурье и Лапласа.

3.1. Спектральный метод анализа линейных цепей

В основе спектрального анализа лежит понятие передаточной характеристики, которая определяет относительный вклад различных спектральных составляющих в формировании выходного сигнала. Для стационарной (с неизменными во времени и пространстве параметрами) линейной системы передаточная характеристика (функция) представляется как отношение в комплексной форме амплитуды гармонических колебаний на выходе x_вых к амплитуде на входе x_вх.

Если правую и левую части формулы для интеграла свертки умножить на , то, интегрируя в пределах то 0 до , можно получить выражение для передаточной функции К(р) дан­ной системы, а также простое алгебраическое выражение, связывающее изображения входного L[х(t)] и выходного сигналов по Лапласу:

(3.4)

После интегрирования получаем

откуда передаточная функция звена

(3.5)

(3.6)

Если правую и левую части формулы для интеграла свертки умножить на и интегрировать обе части уравнения в пределах от до , то произведем преобразование Фурье и получим выражение для частотной характеристики данной системы, а также простое алгебраическое выражение, связывающее изображение выходного и входного сигналов:

(3.7)

После интегрирования получаем

(3.8)

откуда частотная характеристика звена

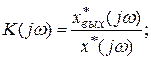(3.9)

.

Следовательно, частотная характеристика звена равна спектру его импульсной характеристики.

Частотная характеристика звена является комплексным числом и представляется в виде суммы действительной и мнимой составляющих:

(3.10)

где — модуль частотной характеристики, или амплитуд­но-частотная характеристика системы; - аргумент частотной характеристики, или фазо-частотная характеристика системы

(3.11)

(3.12)

Любая измерительная система состоит из целого ряда звеньев, соединенных между собой, причем это соединение может быть осу­ществлено:

ü в разомкнутой структуре, которая отличается отсутствием сравнения выхода с входом, последовательно или параллельно;

ü в замкнутой структуре, которая отличается наличием сравне­ния входного и выходного сигналов.

Рассмотрим функции систем в указанных случаях.

Для последовательной разомкнутой структуры выходной сигнал, выраженный через функцию преобразования, запишется как

(3.13)

Для случайного входного сигнала выходной сигнал определяем при известных импульсных характеристиках линейных инерци­онных звеньев:

. (3.14)

Для гармонического входного сигнала изображение выходного сигнала определяем при известных частотных характеристиках звеньев:

(3.15)

Порядок чередования линейных звеньев при их последовательном соединении значения не имеет.

Выходной сигнал системы, состоящей из последовательного сое­динения нелинейных безинерционных звеньев, зависит от поряд­ка чередования звеньев и выражается через операторы звеньев следующим образом:

(3.16)

Для параллельной разомкнутой структуры выход­ной сигнал

(3.17)

В замкнутой структурной схеме выходной сигнал представляется через функции преобразования линейных инерцион­ных звеньев:

(3.18)

При гармоническом сигнале с изображением 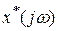изображение выходного сигнала

(3.19)

Основные характеристики звеньев и систем — передаточная, частотная и импульсная — могут быть получены путем преобразо­вания дифференциального уравнения звена, связывающего вход­ной и выходной сигналы.

Если известно дифференциальное уравнение звена с постоянными параметрами

(3.20)

то в этом уравнении заменяют на и на h (t) и затем с помощью преобразования Лапласа определяют передаточ­ную характеристику:

(3.21)

Заменяя р на , получаем частотную характеристику звена

3.2. Анализ линейной цепи методом интеграла наложения (Дюамеля)

Случайный сигнал X (t), действующий на входе линейного звена, в общем случае может иметь любую форму. Задача состоит в определении выходного сигнала Х_вых (t), которая, как известно, решается с помощью интеграла свертки или интеграла Дюамеля. В этом случае сигнал любой формы (рис. 3.1) представ­ляется в виде суммы примыкаю­щих прямоугольных импульсов с амплитудами и длительностями 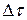. При пре­дельно минимальной величине 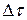каждый из них может быть представлен дельта-функцией с «площадью»

(3.22)

Действие на входе звена еди­ничного импульсного сигнала вызовет соответствующий импульсный выходной сигнал, который про­порционален импульсной характеристике звена — h(t). Функция h(t) должна удовлетворять двум условиям:

ü физической реализуемости h(t) = 0, если t<0;

ü абсолютной интегрируемости для обеспечения асимптотической устойчивости системы .

Суммарный выходной сигнал линейного звена в этом случае на основе принципа суперпозиции состоит из беско­нечной суммы импульсных реакций звена, сдвинутых во времени соответствующим образом, и выражается с помощью интеграла свертки:

. (3.23)

Интеграл свертки, являющийся основой для решения многих практи­ческих задач, можно выразить в двух формах:

(3.24)

.

Интеграл свертки часто удобно представлять не через импульс­ную характеристику звена h(t), а в виде интеграла Дюамеля, че­рез переходную характеристику звена

(3.25)

Рис. 3.1 Представление сигнала в виде суммы дельта-импульсов

В этом случае его можно представить в следующих четырех формах:

(3.26)

Одну из этих форм выбирают в зависимости от того, какое из произведений сомножителей и более удобно для интегрирования.

Однако часто при сложных аналитических формах сигнала, а также при графическом задании входного сигнала трудно аналити­чески определить выходной сигнал. В этом случае рекомендуется применять приближенное определение интеграла свертки.

Если сигнал х(t) задан графически, то представляем его кусоч­но-линейной функцией , состоящей из n участков, на каждом из которых данный участок сигнала х(t) заменяется пря­мой(рис.3.2,а). Затем дифференцируем по участкам функцию и получаем ступенчатую функцию — приближенное выражение первой производной сигнала

Дата добавления: 2017-01-14