Математическое ожидание (среднее значение) ошибки квантования

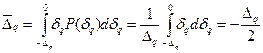. (5.3)

Дисперсия погрешности квантования

D(d_q)= 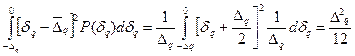(5.4)

При втором способе квантования (рис. 5.2,б) погрешность квантования также подчиняется равновероятному закону, но изменяется в пределах от 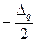до .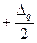

Плотность вероятности ошибки квантования также будет равна

P (d_q) = 1/∆_q.

Математическое ожидание (среднее значение) ошибки квантования 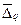= 0.

Дисперсия погрешности квантования

D_q =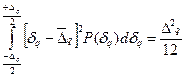

Среднее квадратическое отклонение погрешности при равномерном квантовании

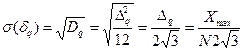(5.5)

Если среднее квадратическое отклонение погрешности задано, то из (5.5) можно определить необходимое при равномерном квантовании число интервалов квантования:

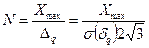(5.6)

Следовательно, необходимое уменьшение погрешности от кван­тования при равномерном квантовании достигается обычно соот­ветствующим увеличением номинального числа уровней квантова­ния.

5.2. Дискретизация

Дискретное представление сигналов во времени называется дискретизацией. При равномерной дискретизации сигнала (см. рис. 5.1,в):

ü ось времени t делится на равно отстающие друг от друга интервалы с шагом Dt;

ü из полученных точек t, 2t, 3t,…, kt проводятся вертикальные линии до пересечения с квантуемой функцией x(t);

ü функция x(t) заменяется совокупностью мгновенных значений амплитуд x₁, x₂, …, x_i, начиная с точки x₀.

Временной интервал D t_k = t_i - t_i-1 между двумя соседними фиксированными моментами времени, в которых задается дискретная функция, называется периодом или шагом дискретизации.

На практике наибольшее распространение получила равномерная дискретизация из-за относительной простоты алгоритма дискретизации и восстановления сигнала и реализующей эти операции аппаратуры. При равномерной дискретизации функции x(t) шаг дискретизации D t постоянен и выбирается на основе априорных сведений о характеристиках сигнала.

При дискретизации непрерывной во времени функции теряет­ся часть информации о ней, но зато в этом случае каждое значение x(t_i) дискретного сигнала строго «привязано» к определенному моменту времени t_{i .}. По этим значениям x(t_i) можно восстановить исходную функцию x(t) с определенной погрешностью. Очевидно, что уменьшение шага дискретизации Dt уменьшает погрешность восстановления исходной функции x(t), но одновременно увеличивает время занятости измерительного канала и требует увеличения его пропускной способности. Поэтому шаг дискретизации Dt выбирают с учетом задаваемой погрешности восстановления исходной функции x(t), которая будет называться воспроизводящей. Оптимальная дискретизация обеспечивает представление исходной функции с заданной точностью минимальным числом отсчетов. В этом случае все отсчеты являются существенными для восстановления исходной функции. Следовательно, дискретизацию по времени следует рассматривать не только как операцию преобразования непрерывного сообщения в дискретное, но и как один из методов устранения избыточной для потребителя информации.

Множество значений амплитуд x(t_i) непрерывной функции x(t), полученное в процессе ее дискретизации по оси t называют дискретным сигналом. Математически дискретные сигналы представляются непрерывной последовательностью чисел, т.е. дискретных функций Х(n). Если дискретная ось t состоит из равноотстоящих отсчетов, то определяемые на этой оси дискретные функции носят название решетчатых (см. рис. 5.1,в). При этом каждой решетчатой функции может соответствовать сколько угодно непрерывных функций, совпадающих с ней при t = k∆t. Эти непрерывные функции называют огибающими данной решетчатой функции. Простейшей огибающей является ступенчатая функция.

Дискретизация непрерывного во времени сигнала являет­ся по сути линейной операцией умножения функции Х(t) на функцию дискретизации во времени:

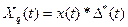(5.7)

Рис. 5.4. Огибающие решетчатой функции

Дискретизация непрерывного во времени сигнала являет­ся по сути линейной операцией умножения функции Х(t) на функцию дискретизации во времени:

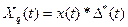(5.7)

Решетчатая функция дискретизации (рис.5.5) ∆ (t) является бесконечной последовательностью единичных им­пульсов (δ – функций Дирака) с периодом повторения T_ц = ∆t, длительностью, равной 0, и площадью, равной единице и может аналитически быть представлена в виде:

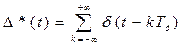, (5.8)

где

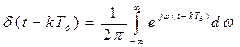. (5.9)

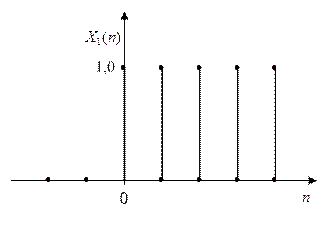
Рис. 5.5. Дискретизирующая функция

Выбор интервалов дискретизации сигнала осуществляется с использованием специальных критериев: частотного критерия В.А.Котельникова, корреляционного критерия Н.А.Железнова, критерия допустимого отклонения воспроизводящей функции от исходной и др.

Математическая модель дискретизированного сигнала может быть представлена тремя способами:

1) в виде импульсной последовательности как скалярное произведение: х_q(t) = 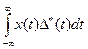= 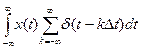(5.10)

2) в динамическом виде:

Х_q(t) = =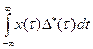

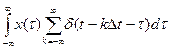
3) в виде алгебраического произведения:

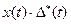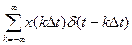
Х_q(t) = = (5.11)

Соответственно математическим моделям получаются различные модели спектра дискретного сигнала.

Для первой модели: S_q(ω) = .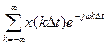

Для последних двух моделей согласно теореме о спектре произведения получаем свертку спектров сигнала S(ω) и спектра дискретизирующей функции S 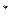(ω):

S_Д(ω) = 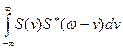(5.12)

Спектр бесконечной периодической последовательности единичных импульсов также единичный и периодический с периодом 2π/∆t:

S 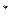(ω) = 2π 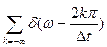. (5.13) Подставив спектр (5.13) в выражение (5.12), получим спектр дискретизированного сигнала периодический и бесконечный.

S_q(ω) = 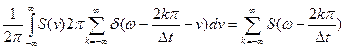. (5.14)

Следовательно, чтобы восстановить сигнал по дискретным значениям, необходимо фильтром нижних частот отфильтровать высокочастотные зеркальные составляющие спектра. Это полностью отвечает теореме Котельникова, согласно которой сигнал может быть полностью восстановлен лишь в диапазоне частот 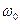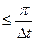, что соответствует периоду дискретизации .

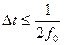При неравномерном квантовании Dt изменяется по случайному закону (стохастически) или с учетом изменения характеристик сигнала (адаптивное квантование). Стохастическая дискретизация является неравномерной со случайными интервалами между отсчетами.

5.3. Квантование по уровню и времени

При квантовании по уровню переход с одного дискретного уровня на другой осуществляется в самые различные моменты времени. При дискретизации, найденные значения непрерывной величины в дискретные моменты времени чередуются через строго определенный интервал времени ∆t, но имеют самый различный уровень.

При квантовании по уровню и времени:

ü вся область возможных значений аналогового сигнала разбивается на конечное число уровней квантования;

ü каждому уровню присваивается определенный индекс (порядковый номер в определенной системе счисления);

ü ось времени t делится на равно отстающие друг от друга интервалы с шагом Dt;

ü значение аналогового сигнала через время Dt внутри интервала квантования, заменяется одним, ближайшим к кривой x(t), уровнем квантования.

На рис. 5.6,а) показан процесс квантования по уровню и времени непрерывного сигнала x(t). На рис.5.6,б) представлена графическая модель погрешности, из которой следует, что для уменьшения суммарной погрешности следует в первую очередь уменьшить шаг дискретизации сигнала.

Суммарная погрешность от квантования определяется как

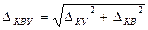. (5.15)

По существу, операция преобразования аналогового измерительного сигнала в цифровую форму имеет место во всех измерительных устройствах, и без ее выполнения принципиально невозможно получить результат измерения в виде конечного числа. В аналоговых измерительных приборах наблюдатель сам осуществляет сопоставление плавно изменяющегося угла отклонения стрелки с делениями шкалы и взятие отсчета. В цифровых измерительных приборах и аналого-цифровых преобразователях эта операция автоматизирована. В цифровых приборах в соответствии со значением измеряемой величины образуется код, а затем в соответствии с кодом измеряемая величина представляется на отсчетном устройстве в цифровой форме.

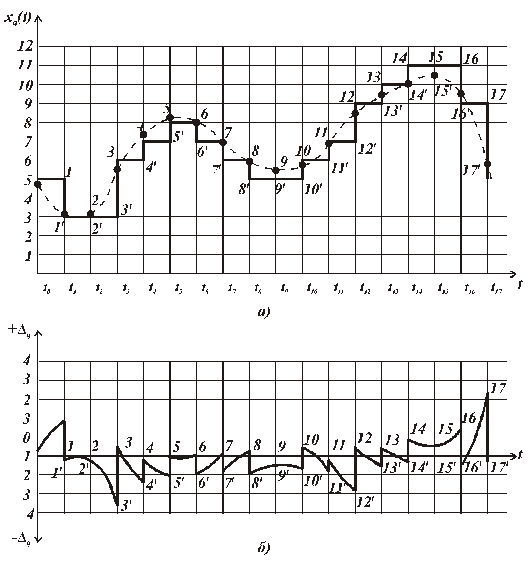
Рис. 5.6. Квантование сигнала по уровню и времени

5.4. Восстановление непрерывного сигнала

Операция дискретизации непрерывного сигнала часто является промежуточным этапом в процессе преобразований сигнала в измерительном цикле. Для многих последующих преобразований сигнала в измерительном канале возникает необходимость получения исходного непрерывного сигнала x(t). Но так как в дискретизированном сигнале отсутствуют промежуточные значения, которые содержались в исходном сигнале, то, следовательно, возникает обратная задача: с заданной погрешностью восстановить все промежуточные значения сигнала x(t) по его дискретным отсчетам. Операция аналитического восстановления исходного сигнала x(t) по его дискретным значениям называется аппроксимацией. Случай, когда восстанавливающая функция x ٭ (t) совпадает с исходной функции x(t) в точках дискретизации и определяются еще дополнительные значения сигнала в пределах шага квантования ∆t, называется интерполяцией. За пределами шага квантования ∆t – экстраполяцией.

В обоих случаях аппроксимации (с интерполяцией или экстраполяцией) сначала выбирают для данного участка сиг­нала восстанавливающую базисную функцию. Полностью восста­навливаемый сигнал будет представлен суммой базисных функций:

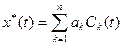, (5.16)

где 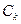(t) — некоторая система базисных функций, которая обыч­но является ортогональной или ортонормированной; 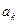— коэффициенты ряда.

В практике аппроксимации наиболее широко применяют три группы базисных функций: степенные полиномы, тригонометрические и экспоненциальные функции.

Оценка степени близости аппроксимирующей функции x ٭ (t) к сигналу x(t) осуществляется с помощью критериев. Распространенными критериями точности являются: критерий Чебышева, основанный на оценке отличия функций x ٭ (t) и x(t) в точках дискретизации (узловых) и критерий по оценке минимальной дисперсии разности этих функций.

Если дискретные значения представлены с невысокой точностью и количество их невелико, то задача оценки точности аппроксимации сводится к методу наименьших квадратов. Пусть сигнал x(t) задан своими дискретными значениями в (n+1) точках t₀, t₁, t₂, … t_n. Восстанавливающая функция при полиноминальной интерполяции запишется в виде:

x ٭ (t) = a₀ + a₁t + a₂t² + … + a_ntⁿ. (5.17)

Для определения неизвестных коэффициентов a₀, a₁, a_2, …, a_n, учитывая условие совпадения в точках дискретизации значений функций x(t) и x ٭ (t), составляем систему уравнений:

a₀ + a₁t₀ + a₂t 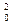+ … + a_nt 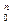= x₀,

a₀ + a₁t₁ + a₂t 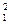+ … + a_nt 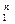= x₁,

………………………………..

a₀ + a₁t_n + a₂t 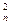+ … + a_nt 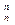= x_n

Определитель этой системы является определителем Вандермонда, он отличен от нуля, а система уравнений имеет единственное решение. Недостаток такого представления функции x ٭ (t) заключается в сложности решения системы уравнений при увеличении числа n и необходимость составления новой системы при изменении числа узловых точек.

Использование для нахождения функции x ٭ (t) интерполяционных формул Лагранжа, Ньютона, Стирлинга, Бесселя и др. как многочленов степени n, с увеличением числа n становятся громоздкими и неудобными в практическом использовании. Поэтому чаще используют кусочную интерполяцию по ограниченному числу точек: ступенчатую, линейную, квадратическую и параболическую.

Аппроксимация функции x(t) по дискретным отсчетам методом ступенчатой интерполяции показана на рис.5.7,а). На рис. 5.7,б) дана графическая модель абсолютной погрешности, возникающей при дискретизации с шагом ∆t. Здесь видно, что заданная величина абсолютной погрешности дискретизации ∆_зад на разных участках достигается за разное время: на одном за ∆t₁, на другом за ∆t₂, а на некоторых она вообще оказывается меньше ∆_зад (например, на участке 5' – 6'). Ясно, что если при выборе шага квантования не учитывать скорость нарастания функции 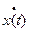, то можно получить большую методическую погрешность + ∆_макс.

Величину абсолютной погрешности ∆зад при расчетах следует принимать как и в случае квантования по уровню либо + ∆зад либо – ∆зад, т.е. в среднем как ∆/2.

При линейной интерполяции (рис. 5.7,в) достаточно соединить отрезками прямых линий точки x₀, 1, 2, …, 17. Полученная ломанная кривая будет с меньшей погрешностью воспроизводить исходную функцию x(t), по сравнению с ступенчатой функцией x ٭ (t).

Экстраполяция, как и интерполяция, может осуществляться различными системами функций, однако на практике чаще используют полиноминальная экстраполяция многочленами Тейлора n-й степени:

x ٭ (t) = 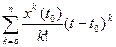, (5.18)

где x^k(t₀) – k –я производная сигнала x(t) в точке t=t₀.

Достоинство многочленов Тейлора заключается в том, в точке t=t₀ все его производные до порядка n включительно совпадают с соответствующими производными сигнала x(t).

При этом полином Тейлора как бы предсказывает (экстраполирует) поведение сигнала x(t) на участке аппроксимации.

Погрешность, возникающая при замене функции x(t) многочленом Тейлора, выражается остаточным членом формулы Тейлора:

∆(t) = 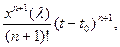(5.19)

где λ – некоторая точка (значение аргумента) лежащая между t и t₀ при t ≠ t₀.

При использовании тригонометрических базовых функций коэффициенты ряда (5.16) опреде­ляются как коэффициенты соответствующего ряда Фурье:

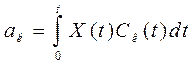. (5.20)

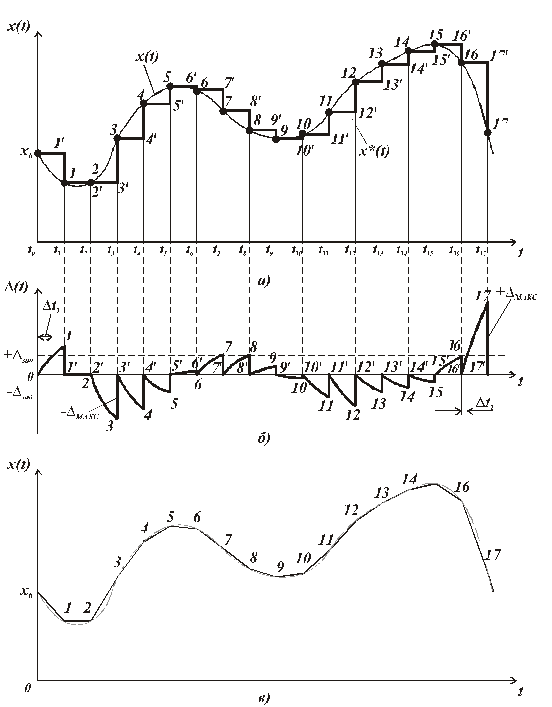
Рис. 5.7. Интерполяция: а) ступенчатая, в)линейная

Координата времени каждой базисной функции в этом случае изменяется во всем диапазоне времени реализации сигнала.

Если в качестве восстанавливающей функции используется ряд Котельникова

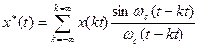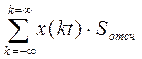= , (5.16)

то базисными функциями в этом ряду являются функции отсчета

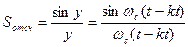, (5.17)

а его коэффициенты равны мгновенным дискретизированным значениям сигнала x(t). График функции отсчетов приведен на рис. 5.8.

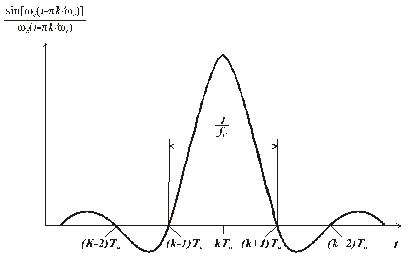
Рис. 5.8. Графическая модель функции отсчетов

Функция отсчетов обладает следующими свойствами:

1) в моменты времени 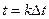достигает максимума, равного 1;

2) в моменты времени 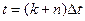, где 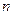— любое целое
число, равна 0;

3) ортогональна на бесконечном интервале времени.

Функция отсчетов представляет собой реакцию идеального фильт­ра нижних частот на входное воздействие в виде единичной импульсной функции. Следовательно, если дискретизированный сигнал с шагом 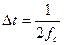подать на вход идеального фильтра с верхней границей пропускания 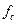, то на выходе получается вос­становленный без погрешностей непрерывный сигнал 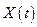. Восста­новление сигнала рядом В. А. Котельникова – случай физического восстановления сигнала. Если выбран шаг дискретизации сигнала по В. А. Ко­тельникову 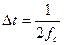, то ввиду бесконечности спектра восстановленный сигнал будет отличаться от исходного, т. е. при восстановлении сигнала возникает погрешность. Она обусловлена следующими причинами:

ü необходимостью ограничения спектра сигнала частотой ;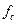

ü погрешностью воспроизведения реальными фильтрами нижних частот функции от­счетов, обладающей бесконечной протяженностью во времени и областью отрицательных значений 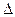t.

Обычно бесконечный спектр сигнала 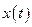ограничивают частотой 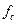, в которой находится боль­шая часть энергии сигнала.

Относительное значение средней квадратической погрешности, возникающей из-за ограничения спектра сигнала частотой 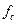, может быть определено из следующего неравенства:

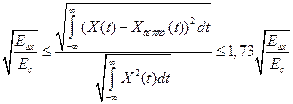, (5.18)

где Х(t) – исходный; x ٭ (t) – сигнал, восстановленный с шагом 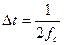; 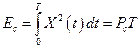– полная энергия сигнала; 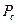– средняя мощность сигнала; 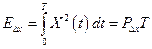– энергия погрешности сиг­нала; 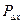— средняя мощность погрешности; 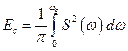– амплитудный спектр сигнала;

– амплитудный спектр погрешности сигнала.

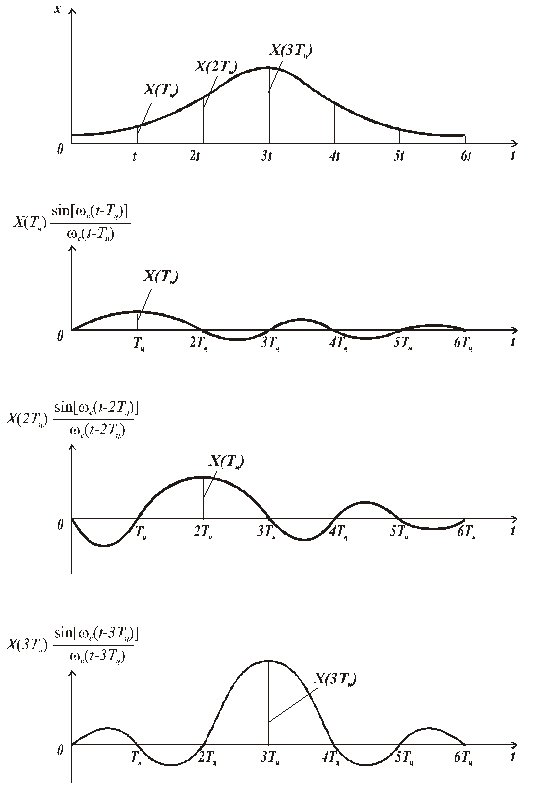
Рис. 5.5. Иллюстрация свойств функции отсчетов

Вопросы для самопроверки

1. Объясните принцип операции квантования по уровню.

2. Объясните два способа квантования сигнала по уровню.

3. Как меняется погрешность квантования по уровню в зависимости от выбранного способа квантования?

4. Как связана погрешность квантования по уровню от числа уровней квантования?

5. В чем сущность операции квантования по времени?

6. Запишите выражение для функции дискретизации во времени.

7. Какие критерии используются для выбора шага дискретизации сигнала?

8. Какие функции используются в качестве воспроизводящих?

9. В чем сущность операции квантования по уровню и времени?

10. Какие требования предъявляются к воспроизведению сигнала?

6. Математическое описание цифровых последовательностей и их преобразований

Физические величины макромира, как основного объекта наших измерений и источника информационных сигналов, как правило, имеют непрерывную природу и отображаются непрерывными (аналоговыми) сигналами. Для дискретизации аналогового сигнала с полным сохранением информации в его цифровом эквиваленте максимальные частоты его спектра должны быть не менее чем вдвое меньше, чем частота дискретизации, то есть f_{ma x} £ (1/2) f_q. Если это условие нарушается, то восстановление аналогового сигнала становится уже невозможным. В целом, много общего в математическом аппарате преобразований аналоговых и дискретных сигналов, но дискретность данных вносит свою специфику в цифровую обработку сигналов. Кроме того, ряд методов дискретной математики не имеет аналогов в аналитической математике. Для анализа дискретных сигналов и систем используется Z - преобразование – математический аппарат анализа цифровых последовательностей, которое является обобщением дискретного преобразования Фурье.

Если дискретной последовательности {x_k} = {x₀, x₁, x₂, …}, k = 0, …, ∞, поставить в соответствие сумму ряда по отрицательным степеням z, то получим Z- преобразование:

X(z) = x₀z⁰ + x₁z^-1 + x₂z^-2 + … = 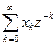. (6.1)

где z – комплексная переменная, X(z) – функция этой комплексной переменной.

Комплексная функция X(z) может быть определена только для тех значений z, для которых степенной ряд (6.1) сходится. Например, для цифровой последовательности вида {x_k} = {1, 2, 0, -1, -2, 0 }, Z- преобразование имеет вид X(z) = 1z⁰ + 2z^-1 + 0z^-2 - 1z^-3 - 2₁z^-4 + 0z^-5 = 1 + 2/z – 1/z³ – 2/z⁴

Обычный способ графического представления z-преобразования состоит в задании особых точек функции X(z): полюсов и нулей. Если x_k является физически реализуемым сигналом, то функция X(z) сходится везде, т.е. во всех точках внутри круга радиуса R. Величина R зависит от положения полюсов функции X(z). Используя графическое представление расположения нулей и полюсов, можно однозначно, с точностью до постоянного множителя, восстановить Z- преобразование. Так если известно, что функция X(z) имеет Q нулей в точках q₁, q_{2, ….} и P полюсов в точках p_1, p₂, … z - плоскости, то она может быть записана либо в виде отношения произведений

X(z)=B ,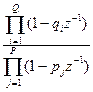

где B – произвольная постоянная, либо в виде дробно-рациональной функции

X(z)=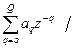

X(z)=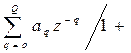

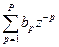
Итак, Z-преобразование дискретного сигнала можно рассматривать как способ его однозначного представления в комплексной z - плоскости. Z-преобразование, выполненное на единичной окружности, т.е. при z = e^jω, совпадает с преобразованием Фурье

X(z) = X(e^jω)= .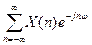

В дальнейшем под обобщенным спектральным анализом будем понимать анализ, дающий точные или приближенные значения параметров Z- преобразования дискретного сигнала для заданных (выбранных) z. Теоретически спектр можно измерять в любой точке z₁ на z – плоскости. В этом случае обобщенный спектр сигнала X(n) можно, согласно (6.1) определить как

X(z) = 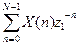, (6.1)

где N – число отсчетов, по которым производится измерение спектра.

На практике наибольший интерес представляют спектральные измерения во множестве точек z – плоскости: z₁, z₂, z_{3, ….} При этом задача измерения спектра сигнала сводится к нахождению значений Z- преобразования конечной реализации сигнала для большого числа точек равномерно распределенных по окружности единичного радиуса (рис.6.1). Такие измерения проводятся путем выполнения дискретного преобразования Фурье для конечной последовательности. Эффективность таких преобразований существенно повышается при использовании быстрого преобразования Фурье.

Основные свойства Z- преобразования:

1. Линейность. Если u_k = ax_k + by_k, то U(z) = aX(z) + bY(z).

2. Смещение цифровой импульсной последовательности (запаздывание на один такт) равнозначно умножению Z-преобразования на z^-1.

Пусть y_k = x_k-1. Тогда Z-преобразование смещенной на разряд последовательности будет равно

Y(z) = 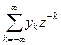= = 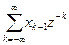z^{-1 .}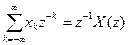

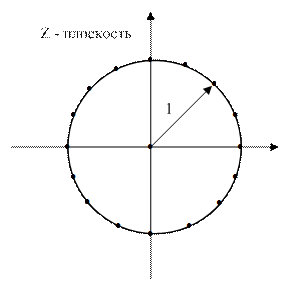
Рис. 6.1. Z – преобразование реализации сигнала

3. Z-преобразование свертки равно произведению Z-преобразования свертываемых аргументов. Если в аналоговом виде свертка сигналов

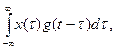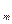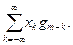
Y(t) = то свертка в в дискретной форме y = Тогда Z-преобразование свертки будет равно

Y(z) =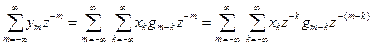

Преобразовав двойную сумму в произведение сумм, окончательно получим

Y(z) = X(z) G(z).

Для восстановления импульсной последовательности применяют обратное Z-преобразование. Если Z-преобразование бесконечной последовательности

X(z) = x₀ + x₁z^-1 + x₂z^-2 +…+ x_mz^-m +

То, умножив обе части на z^m-1, имеем

z^m-1X(z) = x₀ z^m-1 + x₁ z^m-2+… + x_mz^-1 +

Проинтегрировав по z в пределах замкнутого контура, охватывающего все полюсы X(z), согласно теореме Коши, которая гласит, что

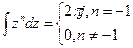получим x_m =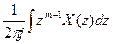

Обратное Z-преобразование равнозначно разложению X(z) в ряд Тейлора по отрицательным степеням z в окрестности точки z^-1 = 0.

Например для экспоненциальной дискретной функции графическое представление Z-преобразования будет иметь вид, представленный на рис. 6.2.

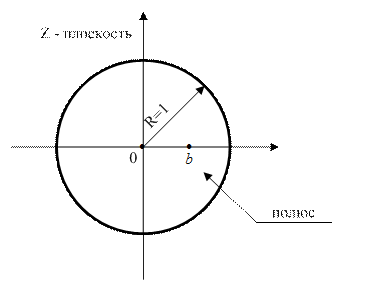
Рис. 6.1. Z-преобразование экспоненциальной дискретной функции

7. Проектирование и реализация цифровых фильтров

Цифровые фильтры относят к классу линейных дискретных систем с постоянными коэффициентами. Проектирование цифровых фильтров включает следующие этапы:

1) синтез ЦФ, заключающийся в определении коэффициентов фильтра на базе выбранного аналогового прототипа;

2) построение структурной схемы;

3) выбор необходимой разрядности исходных данных и процессора;

4) моделирование работы ЦФ;

5) анализ точности обработки измерительной информации.

На этапе синтеза ЦФ используются следующие методы:

1. Метод инвариантных импульсных характеристик. В этом случае импульсная характеристика аналогового прототипа g(t) подвергается дискретизации с постоянным шагом ∆t и принимается g_n= g(n∆t). При конечном n = 0,1,…, N получается нерекурсивный фильтр. Степень приближения частотной характеристики аналогового и цифрового фильтров зависит от частоты дискретизации и порядка фильтра.

2. Метод инвариантных частотных характеристик. Используется преобразование

P= .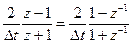

Подставив выражение p в передаточную функцию аналогового прототипа, имеем G(z) =G[p(z)]

На втором этапе проектирования ЦФ осуществляют выбор структурной схемы ЦФ исходя из двух общепринятых типовых структурных схем фильтров.

Трансверсальные, или нерекурсивные (КИХ-фильтры – фильтры с конечной импульсной характеристикой), - это цифровые эквиваленты аналоговых цепей прямого действия. Рекурсивные (БИХ-фильтры – фильтры с бесконечной импульсной характеристикой) – эквивалентны замкнутых (с отрицательной обратной связью) аналоговых цепей.

Нерекурсивный цифровой фильтр (рис. 7.1) реализует следующий алгоритм обработки

Y_k = a₀x_k + a₁x_k-1 + a₂x_k-2 +… + a_mx_k-m ,

где a_k – постоянные коэффициенты. Порядок фильтра определяют числом коэффициентов m. Каждое значение входного сигнала в множительном устройстве умножается на соответствующий постоянный коэффициент a_n, что приводит к погрешности из-за усечения разрядной сетки процессора.

Импульсная и частотная характеристики такого цифрового фильтра соответственно равны

Дата добавления: 2017-01-14