Гаусс теоремасы 4 страница

Идеал газдың тепетеңдіктегі күйінің өзгерісі үшін термодинамиканың бірінші бастамасын мына түрде жазуға болады:

(5.7)

Осы теңдеуді идеал газдардағы изопроцестерге қолданайық. Изопроцесс заңдарын Менделеев-Клапейрона теңдеуінен анықтаймыз.

Изохоралық процесс деп газды қыздыру немесе суыту процестері тұрақты көлемде өтетін процестерді айтады. Термодинамиканың бірінші бастамасы мына түрде болады:

(5.9)

мұндағы – газдың тұрақты көлемдегі мольдік жылусыйымдылығы.

Изобаралық процесс деп газды қыздыру немесе суыту процестері тұрақты қысымда өтетін процестерді айтады:

. (5.10)

Газға изобаралық процесс кезінде берілетін шексіз аз жылу мөлшері :

, (5.11)

мұндағы – газдың тұрақты қысымдағы мольдік жылу-сыйымдылығы. 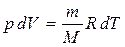. Олай болса:

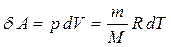. (5.12)

Соңғы өрнектерден:

. (5.13)

Егер (5.13) өрнектен бір моль зат үшін жылусыйымдылық үшін Майер теңдеуі:

. (5.14)

Берілген жылу мөлшері толығымен сыртқы күштерге қарсы жасалатын жұмысқа кетеді:

. (5.15)

Адиабаталық процесс деп жүйелерде сыртқы ортамен жылу алмасусыз өтетін процестерді айтады. кезінде жүйе жұмысты ішкі энергия есебінен жасайды:

. (5.16)

Адиабаталық процестер Пуассон теңдеуімен сипатталады:

, (5.17)

мұндағы – адиабата көрсеткіші немесе Пуассон коэффициенті деп аталатын өлшем бірлігі жоқ шама.

Политроптық процесс – деп С жылусыйымдылықтары өзгеріссіз өтетін термодинамикалық процестерді айтады. Политроп теңдеуінің түрі:

, (5.18)

мұндағы – политроп көрсеткіші ( – берілген процесс үшін газдың жылусыйымдылығы). Жоғарыда келтірілген барлық изопроцестерді политроптық процестердің дербес түрлері ретінде қарастыруға болады. Егер, п =0 болса, онда (5.18) политроптық теңдеу изобаралық процесc (), болса изотермиялық процесc (pV=const), болса, адиабаталық процесс (pV =const) теңдеулеріне айналады.

Термодинамиканың екінші бастамасы

Қайтымды және қайтымсыз процестер

Егер жүйедегі термодинамикалық процесс тура және кері бағытта жүріп, бастапқы қалыпқа қайта оралғанда қоршаған ортада ешқандай өзгеріс болмаса, ондай процесті қайтымды деп атайды.Іс жүзінде, кез-келген термодинамикалық процесс үйкеліс, жылуөткізгіштік, т.б. құбылыстармен қатар жүретіндіктен, жүйе энергиясының бір бөлігі (диссипацияланады) қоршаған сыртқы ортаға тарап кетеді. Сондықтан, нақты процестер әрқашан қайтымсыз болады.

Жылулық қозғалтқыш (машиналар) депжылу энергиясын механикалық жұмысқа түрлендіретін құрылғыны айтады. Кез-келген жылулық қозғалтқыштың жұмыс жасауы үшін қыздырғыш, суытқыш және жұмыс денесі қажет.

Карноның идеал жылулық машинасы

Карно циклі деп тепе-теңдіктегі екі изотермиялық және екі адиабаталық ұлғаюлар мен сығылулардан тұратын қайтымдыдөңгелек процесті айтады. Карно цикліне талдау жасайық.

1) Күй параметрлері 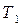, және (5.1–сурет, диаграммадағы нүкте) цилиндр ішіндегі газдың көлемін цилиндрді қыздырғышқа қойып, одан алынған жылу есебінен -ге дейін өте баяу, изотермиялық әдіспен өсіреді.

2) Цилиндрді жылуоқшаулағыш төсенішке қойып, газды адиабаталық түрде ұлғайтады. Газ 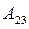жұмысты ішкі энергия есебінен жасайтындықтан, оның температурасы суытқыштың температурасына дейін төмендейді. 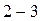қисығы газдың адиабаталық ұлғаюын сипаттайды.

3) Сығылу кезінде жасалған теріс жұмыс жылуға айналып, суытқышқа беріледі. қисығы газдың изотермиялық сығылуын сипаттайды. 4) Цилиндр жылуоқшаулағыш төсенішке қойылған соң, жұмыс денесін адиабаталық түрде одан әрі сығып, бастапқы күйге қайта алып келеді. Бұл процесте газдың температурасы Т2 – ден Т1 – ге дейін өседі. қисығы газдың адиабаталық сығылу процесін сипаттайды. Температурасы қыздырғыштың бірдей болған газды қыздырғышпен қайта жалғап, циклді қайта бастайды. Газдың бір циклде жасаған жұмысы

5.1 – сурет. Карно циклі

Карно теоремасы. Жылулық қозғалтқыш циклінің үнемділігі жылулық пайдалы әсер коэффициенті (ПӘК немесе ) арқылы сипатталады:

. (5.19)

Бірқатар түрлендіруден соң Карно қозғалтқышының ПӘК- ін келесі түрге келтіруге болады:

. (5.20)

Соңғы екі формуладан келесі қатынасты табамыз:

. (5.21)

Олай болса, болғанда ғана болады. Бірақ температураны абсолюттік нөлге дейін төмендету мүмкін емес. Бұл Нернст теоремасы дәлелдеген термодинамиканың үшінші бастамасы. Сондықтан, әрқашан 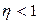болады. Карноның жылулық машинасы – идеал жылу машинасы.

Клаузиус теңсіздігі

немесе .

Теңсіздіктің екі жағын 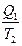бөлшегіне көбейтсек, келесі өрнектерді аламыз

немесе немесе ,

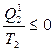Соңғы теңсіздік Клаузиус теңсіздігі деп аталады:

. (5.22)

Энтропия

Жүйенің күйін аз шамаға өзгерту үшін оған қыздырғыштан берілетін элементар жылу мөлшері , ал қыздырғыштың температурасы Т болсын. Егер жүйедегі процесс қайтымды болу үшін, оның температурасы да Т болу керек. Қайтымды процесс кезіндегі келтірілген жылудың элементар мөлшерін dS арқылы белгілейік:

, (5.23)

мұндағы S – энтропия. Жылу мөлшері Q процесс функциясы. Ал, энтропия S күй функциясы болады.

Энтропия – термодинамикалық жүйедегі күйлер ықтималдылығының өлшемі.

Больцман жүйенің термодинамикалық ықтималдылығы мен 2.228. Массасы m = 2,00 кг су t₁ = 10⁰ C-дан t₂ = 100⁰ C- ға дейін қыздырылғанда осы температурадағы буға айналды. Энтропияның өзгерісін табу керек. Судың меншікті жылусыйымдылығы С = 4,2∙10³ Дж/ (кг), ал меншікті булану жылуы 2,25 ∙ 10⁶ Дж/К.

энтропиясы арасында келесі тәуелділік бар екенін дәлелдеді:

. (5.24)

Бұл Больцман формуласы. Жүйенің қандай-да бір күйініің энтропиясы осы күйді тудыратын микрокүйлер санының логарифмімен анықталады.

Нақты газдар мен булар

Қысым үлкен болғанда газ қатты сығылып, молекулалардың көлемдерінің қосындысы газдың көлемімен шамалас болады. Сонымен қатар, молекулалардың бір-бірінен қашықтығы молекуааралық күштерәсер ететін шамаға дейін азаяды.

Нақты газдардың күй теңдеуінде молекулалардың көлемі мен молекулааралық күштер ескерілуі керек. Сондықтан голландиялық физик Ван-дер-Ваальс идеал газ күйінің теңдеуіне екі түзету енгізді:

, (5.25)

мұндағы мен – эксперимент арқылы анықталатын тұрақты шамалар; – газ алып тұрған көлем. Ван-дер-Ваальс теңдеуін шығарарда бірқатар оңайлатулар енгізілгендіктен, бұл теңдеу нақты газ күйін жуықтап сипаттайды. Нақты газ күйін сипаттайтын басқа да теңдеулер бар. Бірақ олар күрделі болғандықтан мұнда қарастырылмайды.

Өзін-өзі бақылауға арналған тесттер:

1. t = 20º C температура кезінде судың тығыздығы судың қаныққан буының осы температурадағы тығыздығынан неше есе (N) үлкен? Осы температурадағы судың қаныққан буының қысымы р = 2,33 кПа.

A) N = 5,9∙ 10³ есе

B) N = 9∙ 10⁴ есе

C) N = 5∙ 10⁴ есе

D) N = 5,9∙ 10⁴ есе

E)N = 5,4∙ 10⁵ есе

2. t = 0º C температурада 1м көлемдегі қаныққан су буы молекулаларының санын (n) табу керек. Берілген температурада судың қаныққан буының қысымы р = 0,61 кПа.

A)

B) .

C)

D)

E)

3. Ван-дер-Ваальстік көмірқышқыл газының сындық күйдегі температурасы мен тығыздығын есептеу керек.

A) 200 К; 0,34 г / см³

B) 400 К; 0,34 г / см³

C) 300 К; 0,34 г / см³

D) 300 К; 5,34 г / см³

E)200 К; 2,34 г / см³

4. Қаныққан су буын идеал газ деп санап, оның 101,0⁰ С кезіндегі қысымын анықтау керек.

A) 2,104 атм; 1,1 К

B) 1,104 атм; 11,1 К

C) 2,104 атм; 3,1 К

D) 1,104 атм; 1,1 К

E)3,104 атм; 2,1 К

5. Массасы 1,00 кг суды 10⁰ С-дан 100⁰ С-қа дейін қыздырғанда ол түгел буланып кетті. Жүйе энтропиясының өзгерісін табу керек.

A) 7,7 кДж / К

B) 9,2 кДж / К

C) 17,3 кДж / К

D) 2,5 кДж / К

E)7,2 кДж / К

6-дәріс

Электр өрісі

Электростатика. Электр зарядтарының өзара әсерлесуі. Электр өрісінің кернеулігі. Гаусс теоремасы. Электростатикалық өрістің жұмысы. Потенциал мен кернеулік арасындағы байланыс. Электрлік сыйымдылық. Конденсаторлар. Диэлектриктер. Поляризациялану. Электрлік ығысу. Электр өрісінің энергиясы. Диэлектрлік қабылдағыштық және оның температураға тәуелділігі.

Тыныштықтағы зарядтардың физикасын қарастыратын электр бөлімін электростатикадеп атайды. Табиғатта электр зарядтары оң және теріс болып екі түрге бөлінеді. Аттас зарядтар тебіледі, ал әр аттас зарядтар тартылады. Табиғаттағы ең кіші электр заряды электрон мен протонның заряды– 1,6×10^-19 Кл. Электрон мен протон массалары сәйкесінше: 9,1×10^-31кг және 1,67×10^-27кг.

Кулон заңы бойынша: вакуумда орналасқан екі және нүктелік зарядтардың өзара әсерлесу күшінің модулі олардың шамаларының көбейтіндісіне тура, ал ара қашықтығының квадратына кері пропорционал:

, (6.1)

мұндағы 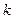-өлшем жүйесіне байланысты болатын пропорционалдық коэфффициент. Векторлық түрде Кулон заңы былай жазылады:

, (6.2)

Материялық ортада Кулон заңы былай жазылады:

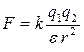, (6.3)

мұндағы -өлшем бірлігі жоқ, ортаның электрлік қасиетін көрсетуші диэлектрлік өтімділік деп аталатын физикалық шама. Вакуум үшін болады. Бірліктердің халықаралық жүйесінде (БХЖ)

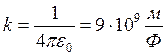, (6.4)

Бұл формуладағы ) немесе Ф/м – электр тұрақтысы деп аталады.

Электрстатикалықөріс кернеулігі

Өріс тарапынан әсер етуші күштің өріске енгізілген зарядтың шамасына қатынасын электр өрісінің кернеулігі деп атайды:

. (6.5)

Немесе:

(6.6)

немесе скаляр түрінде өріс кернеулігі

. (6.7)

Кез келген 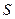ауданнан өтетін векторының ағыны :

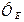(6.8)

болады. Осыған байланысты атап өтетін бір жай: аудан тұйық болған кезде, оған түсірілген нормальдың оң бағыты ретінде сыртқы нормаль алынады: яғни нормальдың бәрі ауданнан сыртқа қарай бағытталады.

:

болады.Электр өрісін 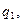…, нүктелік заряд тудыратын болса, онда суперпозиция принципі бойынша қорытқы ағын:

Егер зарядтар тұйық беттің ішіне орналасқан болса, онда теңдіктің оң жағындағы әр интеграл -ге тең болар еді. Сондықтан:

(6.9)

деп жазуға болады. Бұл (6.9) теңдеу Гаусс теоремасының математикалық өрнегi.

1. Электрстатикалық өрісте заряд орын ауыстырғанда орындалатын жұмыс. Нүктелік зарядының өрісінде екінші нүктелік заряд 1-ші нүктеден 2-ші нүктеге қайсыбір траекториямен қозғалсын.

зарядын 1-ші нүктеден 2-ші нүктеге дейін орын ауыстырғанда орындалатын жұмыс:

, (6.10)

мұндағы мен - зарядынан қозғалушы орналасқан бастапқы және соңғы нүктелерге дейінгі қашықтықтар. Егер бірнеше нүктелік зарядтардың өрісінде қозғалатын болса, оған суперпозиция принципі бойынша, күші әсер еткендіктен, атқарылатын жұмыс әр күш жұмыстарының алгебралық қосындысына тең, яғни

, (6.11)

бұл жердегі 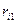мен 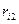мөлшері зарядтан орналасқан бастапқы және соңғы нүктелерге дейінгі қашықтық. Егер қозғалушы зарядты бірлік өлшемді зарядқа тең деп алсақ, онда (6.11) теңдіктен:

,

немесе . (6.12)

Бұл интеграл электрстатикалық өрістің кернеулік векторының тұйық контур бойымен циркуляциясы деп аталады.

Электрстатикалық өріс потенциалы. Потенциалдық өрістегі консервативтік күштер жұмысы потенциалдық энергияның кемуі нәтижесінде орындалады:

. (6.13)

Демек, зарядының заряды өрісіндегі потенциалдық энергиясы:

. (6.14)

Өрістің потенциалы:

. (6.15)

Кернеулік векторы мен потенциал арасындағы байланыc:

немесе , (6.16)

мұндағы - Набла операторы. (11.16) бойынша - кернеулік теріс таңбамен алынған потенциалдың градиентіне тең болады.

Оқшауланған өткізгіштің электрлік сыйымдылығы

Заряд пен потенциал арасында q=Cj тәуелділігі бар екені тәжірибеден белгілі:

. (6.17)

Конденсатор сыйымдылығы:

, (6.18)

Бұдан жазық конденсатордың сыйымдылығы:

, (6.19)

мұндағы – астарлар арақашықтығы; – астарлар арасын толтыратын ортаның диэлектрлік өтімділігі. Цилиндрлік конденсатордың сыйымдылығы:

, (6.20)

мұндағы l – конденсатордың ұзындығы; 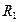мен – ішкі және сыртқы цилиндрлік астарлардың радиустары. Сфералық конденсатордың сыйымдылығы:

, (6.21)

мұндағы 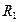мен – ішкі және сыртқы астарлардың радиустары.

Дата добавления: 2017-01-14