Еріксіз электр тербелістері

Енді

.

Лекция

Тербелістер. Гармониялық тербеліс. Еріксіз тербелістер. Резонанс. Толқындар. Геометриялық оптика заңдары. Линза. Жарықтың корпускулалық-толқындық екіжақтылығы. Жарық интерференциясы. Дифракция. Дисперсия. Жарықтың жұтылуы.

Тербелмелі контур. Актив кедергісі жоқ контурдағы еркін тербеліс

Индуктивтігі мен сыйымдылығы бар тізбекте электр тербелісі пайда бола алады. Мұндай тізбек тербелмелі контур деп аталады. 3.2-суретте идеалды актив кедергісіз контурдағы (тербелмелі контурдағы) тербелмелі процестің жүйелі сатылары көрсетілген.

18.2-сурет. Тербелмелі контурдағы тербеліс процесінің жүйелі сатылары.

Актив кедергісі жоқ контурдағы тербеліс теңдеуі:

. (10.1)

Бұл теңдеудің шешуі:

q=q_mcos(wt+a). (10.2)

Тербелістің периоды Томсон формуласынан анықталады:

. (10.3)

(18.37)теңдеуін дифференциялдап ток күшінің өрнегін табамыз:

І=-w₀q_m×sіn(wt+a)=І_m×cos(wt+a+p/2). (10.4)

Конденсатордағы кернеу зарядтан 1/С көбейткішке өзгеше

U=q_m/C×cos(wt+a)=U_m×cos(wt+a). (10.5)

Еркін өшпелі тербелістер

Нақты тербелмелі контурда әрқашанда актив кедергі болады. Контурда жинақталған энергия біртіндеп осы кедергілерде шығындалады, соның есебінен еркін тербеліс өшеді.

1-3-2 тізбек үшін жазылған (10.1) өрнектің түрі (10.1-сурет):

. (10.6)

Бұл теңдеуді L-ге бөліп, І-ді q-мен алмастырып, -ны -мен

белгілеп жазсақ:

. (10.7)

10.1-сурет. Нақты тербелмелі

контурдың сұлбасы.

теңдеуін аламыз. b= R/2L белгілеу енгізсек және LC-ға кері шама контурдың меншікті циклдік жиілігінің w₀ квадраты екенін ескеріп (10.7) өрнегін мынадай түрда жазуға болады:

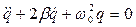. (10.8)

Егер яғни R²/4 L²< 1 / LC болса, онда (10.8)теңдеуінің шешуі:

(10.9)

болады, мұндағы ; w₀ мен b мәндерін қойсақ:

(10.10)

өрнегін аламыз. Конденсатордағы кернеу:

. (8.11)

Ток күші:

Бұл формуланың оң жағын бірге тең шамаға көбейтсек, алатынымыз:

.

шарттарымен анықталатын y бұрышын енгізіп, ток күшін

(10.12)

түрінде жаза аламыз.

Тербелістің өшуін өшудің логарифмдік декременті:

, (10.13)

мұндағы а(t) қандай да бір шаманың амплитудасы.

Еріксіз тербеліс болуы үшін, сырттан жүйеге периодты түрде әсер ету керек. Оның теңдеуі:

. (10.14)

Бұл теңдеудің шешуі:

q = q_m× cos(wt -y). (10.15)

Электромагниттік өріс үшін толқындық теңдеу

Максвелл теңдеулерінен электромагниттік толқын үшін төмендегі теңдеулерді табуға болады:

(10.16)

Мысалы, бастапқы ток – электромагниттік толқын көзі – гармониалық заңдылықпен өзгеретін болса (І=І₀×cosωt), онда (8.16) теңдеуінің шешімі:

, (10.17)

мұндағы Е₀ мен Н₀ – өрістердің амплитудалық мәндері; w – тербелістің циклдік жиілігі; v – электромагниттік толқынның жылдамдығы.

Кез келген электромагниттік толқындар вакуумда тұрақты жылдамдықпен тарайды:

м/с.

Материялық ортадағы жарық жылдамдығы:

, (10.18)

мұндағы Ф/м, = 12,56×10^-7 Гн/м – тұрақты шамалар, ал e және m– заттың диэлектрлік және магнит өтімділігі. – мөлдір диэлектриктің сыну көрсеткіші деп аталады, мұндай заттардың көпшілігі үшін m= 1, яғни n= , онда

.

Бұдан жарық толқынының ұзындығы вакуумнан затқа өткенде өзгереді деген қорытынды шығады. Өйткені, , онда вакуумда , ал , демек

. (10.19)

Геометриялық оптика

Жарықтың шағылу және сыну заңдары

Жарықтың түзу сызықты таралу заңы: оптикалық біркелкі ортада жарық сәулесі түзу сызық бойымен таралады. Егер сыну көрсеткіші барлық жерде бірдей болса, ондай орта оптикалық біртекті орта деп аталады. Бұл заң жарық сәулелерінің таралу жолына қойылған экранда дененің геометриялық көлеңкесінің пайда болуымен дәлелденеді.

Жарық шоқтарының тәуелсіздік заңы: Бір нүктеге түскен жарық сәулелері бір-біріне тәуелсіз болады. Нүктенің жарық интенсивтілігі әрбір жарық сәулесінің интенсивтіліктерінің қосындысына тең:

.

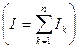10.1-сурет. Жарықтың екі орта шекарасынан шағылуы және сынуы.

Жарықтың шағылу заңы: шағылу бұрышы i ′₁, түсу бұрышы i ₁-га тең болады (i ₁= i ′₁), түскен сәуле, шағылған сәуле және түсу нүктесіне тұрғызылған перпендикуляр бір жазықтықта жатады.

Жарықтың сыну заңы:

а) шағылған сәуле, сынған сәуле және изотропты, біртекті екі орта шекарасына тұрғызылған перпендикуляр бір жазықтықта жатады;

б) екі орта үшін түсу бұрышының i ₁ синусының сыну бұрышының i ₂ синусына қатынасы тұрақты шамаға тең, ол бірінші ортадағы жарық жылдамдығының екінші ортадағы жарық жылдамдығына қатынасына тең болады:

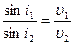. (10.20)

Ортадағы жарық жылдамдығы мен вакуумдағы жарық жылдамдығы арасында тәуелділік болатындықтан,келесі теңдік орындалады:

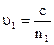және , (10.21)

мұндағы және – жарық таралатын орталардың абсолют сыну көрсеткіштері; және – жарық толқындарының фазалық жылдамдықтары.

Жарық толқындарының интерференциясы

Екі тербелістің қосылуын қарастыралық

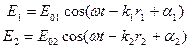, (10.22)

Бұл бөліктер бір ғана толқынның бөлігі, олай болса, және , толқындық векторлар әртүрлі болады: және , өйткені бұл екі толқын және жол жүруі мүмкін. Олардың сыну көрсеткіштері , . Онда бұл когерентті толқындардың фаза айырымы

, (10.23)

мұндағы 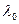− вакуумдағы толқын ұзындығы, − жарық толқынының оптикалық жол айырымы. Сонымен, фаза айырымы мен оптикалық жол айырымы арасындағы байланыс:

. 10.24)

Интерференциялық максимум:

. (10.25)

Интерференциялық минимум:

. (10.26)

Жарықтың дифракциясы

Жарықтың дифракциясы - деп біртекті емес ортада (мәселен, экрандағы тесіктерден және мөлдір емес шекара маңында) таралғанда байқалатын жарықтың толқындық қасиетттерінің жиынтығын айтамыз. Гюйгенс- Френель принципі бойынша S толқын бетініңәр элементі dS (10.2-сурет), амплитудасы элемент ауданына пропорционал болатын екінші реттік сфералық толқын көзі болып табылады. Сфералық толқынның амплитудасы толқын көзінен r арақашықтыққа кері пропорционал заңы бойынша өзгереді. Сондықтан

Шеңберлерден Р нүктесіне дейінгі қашықтықтарды бір-бірінен жарты толқын ұзындығына l/2-ге артық болатындай етіп салайық.

10.2-сурет. Френель зоналары.

Суретте көрсетілгендей, m-ші зонаның сыртқы шетінен Р нүктесіне дейінгі қашықтық b _m мынадай:

b _m = b + ml/2, (10.27)

мұндағы b − толқын бетінің О төбесінен Р нүктесіне дейінгі қашықтық. Екі көрші зонадан Р нүктесіне келіп жететін тербелістер қарама-қарсы фазада болады. Сондықтан да әр зонадан келіп түскен толқындардың көрші зонадан түскен толқындармен фаза айырымы p- ге тең болады.

Френель зоналарының ауданын есептейік. m-ші зонаның сыртқы шекарасы толқын бетінде биіктігі h_mсфералық сегмент құрайды (10.3-сурет).

10.3-сурет. Френелдің m -ші зонасы.

m-ші Френель зонасының сыртқы шекарасы радиусы:

. (10.28)

Жарық дисперсиясы

Жарықтың дисперсиясы деп заттың сыну көрсеткішінің толқын ұзындығына тәуелділігін айтады.

шамасы заттың дисперсиясы деп аталады, ол толқын ұзындығы бойынша сыну көрсеткішінің өзгеру жылдамдығын көрсетеді. Толқын ұзындығы азайған сайын монотонды түрде өседі, сондықтан 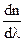модуль бойынша l кеміген сайын артады. Мұндай дисперсия нормаль дисперсия деп аталады. Егер зат сәулелердің бөлігін жұтатын болса, онда жұту аймағы мен оның маңында дисперсия жүруі аномальді түрде болады, сондықтан ол аномаль дисперсия деп аталады.

Жарықтың жұтылуы

Заттағы жарық жұтылуы Бугер заңымен сипатталадыі:

, (10.29)

Поляризацияланған және поляризацияланбаған жарық. Малюс заңы

Егер жарық векторының бағыттары қандай да бір тәсілмен реттелген болса, онда жарық поляризацияланған деп аталады,

Кәдімгі жарықта бұл бағыттар тұрақты түрде өзгереді. Мұндай жарық поляризацияланбаған жарық болып табылады.

Поляризация дәрежесі келесі өрнек арқылы анықталады:

. (10.30)

Электр өрісі кернеулік 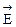векторының тербеліс амплитудалары поляризация жазықтығында үлкен мәнге ие болады. Мұндай жағдайда I_min=0 болып, ал поляризация дәрежесі бірге тең болады, яғни Р=1. Табиғи жарық үшін I_max=I_min және Р=0.

I ₀ поляризацияланған жарықтың интенсивтігін I _р деп, ал I анализатордан өткен жарықтың интенсивтігін I _А деп белгілейік:

. (10.31)

(10.31) өрнегі Малюс заңы деп аталады.

Шағылған толқын толық болғанда толық поляризацияланады. Сынған және шағылған сәулелер арасындағы бұрыш 90⁰ болатындықтан:

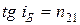. (10.32)

(10.32) өрнегі Брюстер заңы деп аталады. Шағылған жарықта тек қана түсу жазықтығына перпендикуляр поляризацияланған толқын болады, і = і_Б бұрышы толық поляризация бұрышы не Брюстер бұрышы деп аталады.

ы k − пропорционалдық коэффициенті Керр тұрақтысы деп аталады; ол заттың температурасы мен жарық толқынының ұзындығына тәуелді. Керр ұяшығын айқышталған поляризаторлар арасына қойып, оған импульсті кернеу беретін болсақ, жүйе арқылы өтетін жарықты басқаруға болады. Жарықты қайтадан қосу уақыты өте аз шама - шамамен 10^-12 с болады.

Өзін-өзі бақылауға арналған тесттер:

1. Екі жағы да ашық U-тәріздес түтікке 0,24 кг сынап құйылды. Түтік радиусы r = 5 мм. Түтіктегі сынап тербелісінің ω циклдік жиілігін есептеңіз. Сынаптың тұтқырлығын елемеуге болады.

A)

B)

C)

D)

E)

2.τ = 480c уақыт аралығында өзінің механикалық энергиясының 99 % пайызын жоғалтатын, математикалық маятниктің β өшу коэффициентін табыңыз.

A)

B)

C) .

D)

E)

3. Жарық күші I₀ = 100 кд нүктелік жарық көзі фокус-тық арақашықтығы f = 25,0 см, шағылдыру коэффициенті 0,80 ойыс айнаның төбесінен s = 20,0 см арақашықтықта орналасқан. Шағылған шоқтағы жарық күшін анықтау керек.

A)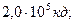

B)

C)

D)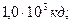

E)

4. Фокустық арақашықтықтары f₁ = 7 см және f₂ = 6 см екі жұқа линза бір-бірінен d = 3 мм арақашықтықта орналасқан. Жүйенің фокусы аталған линзалардың екінші-сінен қандай арақашықтықта орналасады?

A)5,1 см

B) 2,4 см

C)3,2 см

D)1,6 см

E)3,5 см

5. Жұқа қабыршыққа (n=1,33) ақ жарықтың параллель шоғы түседі. Түсу бұрышы 52⁰. Қабыршықтың қандай қалыңдығында айналық шағылған жарық сары түске ( мкм) барынша күшті боялады?

A)b = 1,4 (1+2 к) мкм, к=0,1,2……;

B) b = 2,14 (1+2 к) мкм, к=0,1,2……;

C) b = 0,14 (1+2 к) мкм, к=0,1,2……;

D)b = 3,14 (1+2 к) мкм, к=0,1,2……;

E)b = 4,14 (1+2 к) мкм, к=0,1,2……;

6. Сыну көрсеткіші n=1,33 қабыршықтан толқын ұзындығы 0,64 мкм жарық барынша күшті шағылады, ал толқын ұзындығы 0,40 мкм жарық мүлдем шағылмайды. Жарықтың түсу бұрышы 30⁰ болса, қабыршықтың ең аз қалыңдығы қандай болғаны?

A)0,55 мкм

B)0,60 мкм

C)0,45 мкм

D)0,75 мкм

E)0,65 мкм

11-дәріс

Жылулық сәуле шығару.Фотоэффект. Комптон эффекті. Де-Бройль гипотезасы. Электрондар дифракциясы. Толқындық функция және оның статистикалық мағынасы. Микробөлшектердің толқындық қасиеттері және анықталмаушылық қатынастары.

Дененің ішкі энергиясы есебінен шығатын сәулені жылулық сәуле шығаруы деп атайды.

Денелердің сәуле шығару қабілеті деп уақыт бірлігі ішінде дене бетінің аудан бірлігіне келетін жиіліктері -ден +d аралығында шығарылатын электромагниттік сәуле шығарудың dW_сәуэнергиясын айтады.Сонымен,

Е(,Т) = dW_сәу/ d (11.1)

ХБЖ жүйесінде сәуле шығарғыштық қабілетінің өлшем бірлігі ретінде [Дж/м²] алынған.

Электромагниттік толқындар жұтылуының спектрлік сипаттамасы – денелердің жұту қабілеті А(ν,Т):

А(ν,Т) = dW_жұт/dW. (11.2)

Егер кез-келген температурада және барлық жиіліктер үшін А(ν,Т)=1 болса, онда дене абсолют қара дене (АҚД) деп аталады. Абсолют қара дененің сәуле шығару қабілетін ε(ν,Т) деп белгілейміз. Ол дененің сәуле шығару жиілігіне және абсолют температурасына тәуелді.

Абсолют қара а дене үшін

dW_шығ= ε(ν,Т) dν, (11.3)

Термодинамикалық тепе-теңдік күйінде dW_шығ =dW_жұт, олай болса:

E(ν,Т)/ А(ν,Т)= ε(ν,Т). (11.4)

Сәуле шығару қабілетінің оның жұту қабілетіне қатынасы дененің химиялық құрамына тәуелді болмайды және ол абсолют қара дененің сәуле шығару қабілеті болып, ол температура мен жиіліктің f(ν,Т) функциясы болып табылады. Бұл заң Кирхгоф заңы деп аталып, ал ε(ν,Т) функциясы Кирхгоф функциясы деген атқа ие болды.

Бірақ Л.Больцман термодинамикалық әдіспен теориялық абсолют қара дене:

(11.5)

үшін дұрыс болатындығын көрсетті. Сондықтан, бұл тәуелділік физика тарихында Стефан-Больцман заңы деп аталады. Абсолют қара дененің энергетикалық жарқырауы абсолют температураның төртінші дәрежесіне тура пропорционал ( σ=5,67∙10^-8(Вт/м²К⁴ − Стефан-Больцман тұрақтысы).

Виннің ығысу заңы:

. (11.6)

Заңның тұжырымы: абсолют қара дененің сәуле шығару қабілетінің максимум мәніне келетін жиілік оның абсолют температурасына тура пропорционал болады.

Әдетте Виннің ығысу заңын сәуле шығарудың толқын ұзындығы арқылы жазады:

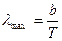, (11.7)

мұндағы − абсолют қара дененің сәуле шығару қабілетінің максимум мәніне келетін толқын ұзындығы, ол температураның өсуіне байланысты қысқа толқын ұзындығына қарай ығысады. b − Вин тұрақтысы ( мК) деп аталады, ол тәжірибелік жолмен анықталады.

Рэлей-Джинс өрнегі:

ε(ν,Т) = (2πν²/c²) kT. (11.8)

Рэлей және Джинс көзқарастарының негізінде абсолют қара дененің энергетикалық жарқырауы:

= = = 2πkT/c^{2 2} d ν = .

Бұл қайшылық ультракүлгін апаты деп аталды. Сонымен, Рэлей-Джинс өрнегі Стефан-Больцман заңына = Т⁴ қайшы келеді. Бірақ, Рэлей және Джинс еңбектері ешқандай нәтиже бермейді деп ойлауға болмайды.

Бұл қиындықтан шығуды 1900 жылы неміс физигі М. Планк тапты. Планк былай деп ұйғарды: осциллятордың сәуле шығару энергиясы тек белгілі дискретті мәндерді қабылдауы мүмкін, ол мәндер энергияның элементар үлесінің бүтін санына тең болады, яғни кванттарға тең. Сондықтан, осциллятор энергиясын мына түрде беруге болады 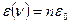, мұндағы 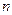− кез келген бүтін оң сан. Бұл шарт кезінде Больцман таралуын пайдаланып, Планк формуласын аламыз:

. (11.9)

Дата добавления: 2017-01-14