Комптон эффекті

Фотоэффект

Ішкі фотоэффект − жартылай өткізгіштің ішінде жарықтың әсерінен атомдармен байланысқан электрондар атомнан босап шығып, бірақ өткізгіш бетінен сыртқа шықпайды. Ол жартылай өткізгіштің электрөткізгіштігін арттырады, өйткені жартылай өткізгіш ішінде еркін электрондар саны артады.

Сыртқы фотоэффект деп қатты және сұйық заттардан жарық әсерінен электрондарды бөліп шығаруды айтады.

Планктың кванттық гипотезасын дамыта келіп, А.Эйншейн тендеулер түрінде фотоэффектінің келесі сұлбасынұсынды. Энергиясы болатын фотон, металл бетін атқылап электронмен соқтығысады жєне толығымен өзінің барлық энергиясын (23.7-сурет) береді.

Бұл кезде фотон энергиясы металдан электронның шығу жұмысына және оған кинетикалық энергия беруге жұмсалады. Онда фотоэффект үшін энергияның сақталу заңы мына түрде жазылады:

. (11.10)

Соңғы тендеу фотоэффект үшін Эйнштейн тендеуі деп аталады.

Жарықтың кванттық қасиеттері 1923 жылы А. Комптон байқаған құбылыста да білінеді. Комптон эффекті деп рентген сәулелерінің (рентгендік кванттар) металл атомдарынан шашырауы нәтижесінде, оның толқын ұзындығының өзгеруін айтады.

Шашыраған сәулелердің толқын ұзындығы, түсетін сәулелердің толқын ұзындығынан 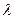едәуір үлкен болатынын, сонымен бірге айырымы тек θ шашырау бұрышына тәуелді екенін комптон тәжірибелері көрсетті:

, (11.11)

мұндағы 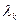тұрақтысы − Комптон толқын ұзындығы деп аталады: .

Атомдардың сызықтық спектрлері. Бор постулаттары.

Бордың бірінші постулаты: атом, кейбір стационар күйлерде өзінен электромагниттік толқын (жарық) энергиясын шығармайды және жұтпайды.

Бордың екінші постулаты: бір стационар күйден екінші стационар күйге көшкенде атом бір квант энергиясын шығарады немесе жұтады. Бұл постулат жиіліктер ережесі болып табылады және оны келесі түрде өрнектеуге болады: атом бір стационар күйден екінші стационар күйге көшкенде, стационар күйлердің энергиялар айырымына тең болатын һn квант энергиясын шығарады немесе жұтады, яғни

(11.12)

Импульс моментінің квантталуы: атомның стационар күйіндегі электрон, импульс моменті Планк тұрақтысына еселік болатын дөңгелектік орбита бойынша қозғалады, яғни мына шартты қанағаттандырады:

, (11.13)

мұндағы m – электрон массасы, – электрон жылдамдығы, r – электрон орбитасының радиусы, , n=1,2,3,… – сутегі атомының энергетикалық деңгейлерінің ретін анықтайтын бүтін сандар, олар бас кванттық сандар деп аталады.

Сутегі атомындағы электронның n-ші орбитасының радиусы:

. (11.14)

Соңғы теңдеуден, орбита радиусы бүтін сан квадратына n² пропорционал түрде өсетіндігі көрінеді. Сутегі атомындағы электронның толық энергиясы оның кинетикалық және потенциялық энергияларының қосындысынан тұрады. Электронның кинетикалық энергиясы мына өрнек бойынша анықталады:

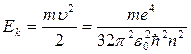. (11.15)

Сутегі атомындағы электронның потенциялық энергиясы мынаған тең:

. (11.16)

Сутегі атомындағы электронның толық энергиясы:

. (11.17)

Микродүниеде бөлшектің күйі толқындық функция арқылы сипатталады. Толқындық функцияның модулінің квадраты көлемде бөлшектің t уақытта болу ықтималдығына пропорционал болады:

. (11.18)

Ықтималдық тығыздығы

. (11.19)

Гейзенбергтің анықталмаушылық қатынастары:

(11.20)

.

Өзін-өзі бақылауға арналған тесттер:

1. Калийге толқын ұзындығы = 330 нм жарық түсіргенде шығатын фотоэлектрондар үшін тежеуші потенциалды анықтау керек.

A)λ = 214 нм

B) λ = 204 нм

C)λ = 244 нм

D)λ = 325 нм

E)λ = 312 нм

2. Комптон эффектісінде фотонның шашырау бұрышы =90⁰, электронның тебілу бұрышы =30 ⁰. Фотонның шашырағанға дейінгі энергиясын анықтау керек.

E _f = E₀ cos(α+ θ/2) / [sinαsin(θ/2)];

A) 1,37 МэВ

B) 2,37 МэВ

C) 0,37 МэВ

D) 3,37 МэВ

E) 0,7 МэВ

3. Қарқындылығы І = 0,20 Вт/см² параллель жарық шоғы шағылдыру коэффициенті жазық айнаға бұрышпен түседі. Жарықтың айнаға түсіретін қысымын анықтау керек.

A) p = 7,17 мкПа

B) p = 6,17 мкПа

C) p = 5,17 мкПа

D) p = 4,17 мкПа

E) p = 3,17 мкПа

4. Массасы М, радиусы r₀ жұлдыз жиілігі фотон шығарады. Фотон жиілігінің жұлдыздан өте алыс арақашықтықтағы гравитациялық ығысуының шамасын табу керек.

A) Δ / = exp[- M / (c² r_о)

B)Δ / = exp[- / (c² r_о)

C)Δ / = exp[- M / (cr_о)

D)Δ / = exp[- M / (c²)

E) Δ / = exp[-M / (c² r_о)

5. Энергиясы МэВ рентген сәулесінің фотоны тыныштықтағы бос электроннан шашырайды. Нәтижесінде рентген сәулесінің толқын ұзындығы –ге артты. Тебілген комптондық электрон ұшып шыққан бұрышты табу керек.

A) 45⁰

B) 39 ⁰

C) 59⁰

D) 49 ⁰

E) 55⁰

12-дәріс

Шредингердің уақыттық және стационар теңдеуі.

Бір өлшемді тікбұрышты шұңқырдағы бөлшек.

Бөлшектің потенциалдық тосқауыл арқылы өтуі.

Кванттықтеориядағыатомжәнемолекула.

Шредингердің уақыттық теңдеуі:

, (12.1)

мұндағы m – бөлшектің массасы, Дж×с – 2p-ге бөлінген Планк тұрақтысы, – жорамал сан, Ψ(x,y,z,t) – толқындық функция, U(x,y,z,t) – күштік өрістегі бөлшектің потенциялдық энергиясы, – Лаплас операторы.

(12.1) Шредингер теңдеуі жалпы жағдай үшін шешілмейді. Бірақ, бұл теңдеудегі потенциялық энергия уақытқа тәуелсіз, яғни бөлшек қозғалатын күштік өріс стационарлы болcа

. (12.2)

Бұл Шрёдингердің стационарлық теңдеуі.

Мұндай қозғалыстың, мысалы ретінде металл ішіндегі электрондардың қозғалысын қарастыруға болады. Бұл жағдайда металл сыртындағы электрон ның потенциалдық энергиясы нөлге тең. (2121-суреттегі І және ІІІ аймақтар – шұңқыр сырты |x|>a, U=0), ал металл ішіндегі потенциялы теріс мәнге ие және электронның металдан шығу жұмысына тең (12.1 суреттегі ІІ аймақ, шұңқыр іші, |x|<a, U=-U₀).

12.1-сурет. Бірөлшемді потенциалдық шұңқыр.

Потенциалдық шұңқырдың ені 2а. Электрон қозғалысы бір өлшемді болғандықтан (ОХ осі бойымен), толқындық функция тек х осіне тәуелді болады және Лаплас операторының түрі . Е<0 екенін ескеріп, Шредингер теңдеуін І, ІІІ аймақтар және ІІ аймақ үшін мына түрде жазамыз:

IжәнеIII: , (12.3)

II: 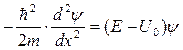. (12.4)

(12.4) теңдеуін келесі түрде жазайық

және

(12.5)

деп белгілейік. Олай болса І және ІІІ аймақтар үшін Шредингер теңдеуі мына түрге келеді

. (12.6)

Бұл теңдеудің шешуі келесі түрдегі толқындық функция болып табылады:

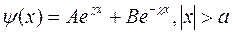. (12.7)

ψ(х) функциясы шекті функция, олай болса х=±¥ мәндерінде ψ(х) шекті болуы үшін А=В=0

Енді потенциалдық шұңқыр ішіндегі (ІІ аймақ) электрон қозғалысын қарастырайық. Ол үшін (11.8) теңдеуін мына түрде жазайық

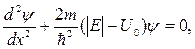
, (12.8)

мұндағы

. (12.9)

Толқындық функцияның үздіксіз шарттарынан потенциалдық шұңқырдың шекарасында келесі шарттар шығады

. (12.10)

Алынған (12.10) теңдеулерін мүшелеп қосып coska =0 аламыз, ал бұл кезінде орындалады.Энергия:

. (12.11)

Өзін-өзі бақылауға арналған тесттер:

1. Анықталмағандық қатысын пайдаланып өлшемі l = 0,20 нм аймақта қозғалған электронның ең аз кинетикалық энергиясын бағалау керек.

A) 2,5 эВ

B) 2 эВ

C)1,5 эВ

D) 1 эВ

E) 0,5 эВ

2. Анықталмағандықтар қатыстарын пайдаланып сутегі атомындағы электронның мүмкін болатын ең аз энергиясын және оның ядродан сәйкес тиімді арақашықтығын бағалау керек.

A) 52 пм, -3,6 эВ

B) 53 пм, -13,6 эВ

C) 52 пм, -1,36 эВ

D) 43 пм, -13,6 эВ

E) 33 пм, -13,2 эВ

3. Потенциалдық жәшіктегі бөлшек негізгі күйде тұр. а)жәшіктің ортаңғы үштен бірінде, б) жәшіктің шеткі үштен бірінде бөлшектің табылу ықтималдығы қандай?

A) 0,60; 0,5

B) 0,9; 0,295

C) 0,6; 0,15

D) 0,609; 0,195

E) 0,09; 1,95

4. Электрон ені l бірөлшемді потенциалдық жәшікте орналасқан. Бірінші энергетикалық деңгейдегі электронның жәшік қабырғаларынан бірдей l /4 аралықтан табылу ықтималдығын есептеу керек.

A) 4,475

B) 3,475

C) 2,475

D) 0,475

E) 1,475

5. Бөлшек ені l потенциалдық жәшікте eң төменгі қозған күйде тұр. Бөлшектің жәшік қабырғаларынан бірдей l /4 аралығында табылу ықтималдығын анықтау керек.

A) 0,91

B) 0,091

C)0,0091

D) 1,91

E) 0,1

6. Бір өлшемді ені l потенциалдық шұңқырдың қабырғаларынан l /4 бірдей арақашықтықтағы бірінші және екінші энергетикалық деңгейлердегі электронның табылу ықтималдықтарының ω₁/ω₂ қатынасын есептеу керек.

A) 8,22

B) 7,22

C) 6,22

D) 5,22

E) 4,22

13-дәріс

Сутегі атомы үшін Шредингер теңдеуі. Сутегі тектес атомдар.

Энергия деңгейлері. Күрделі атомдардағы электрондық

деңгейлердің құрылымы. Паули принципі

.Сутегінің молекуласы. Иондық және коваленттік байланыстар.

Кванттық-механика тұрғысынан сутегі атомын, протонның (ядроның) потенциалды өрісіндегі электронның қозғалысын қарастырылатын есепке келтіреміз. Сутегі атомындағы электронның потенциалдық энергиясы мына өрнекпен сипатталады:

. (13.1)

Шредингердің стационарлық теңдеуі:

. (13.2)

Электрон массасы ядро массасынан көп кіші болғандықтан, есепті қозғалмайтын ядроға қатысты электрон қозғалысы ретінде қарастырып және қозғалыс орталық сфералық симметриялы өрісте өтетіндіктен, сфералық координат жүйесін (r,q,j) пайдалану дұрыс болады:

өрнегін пайдаланып, сфералық координаттардағы Шредингер теңдеуін жазайық

. (13.3)

Бұл теңдеуді шешу жолдары жалпы физика курсында қарастырылмайды, бірақ біз сутегі атомындағы электрон қозғалысын талдау үшін теңдеуді шешу барысында алынған нәтижелерді пайдаланамыз.

(13.3) Шредингер теңдеуін шешу барысында алынған маңызды нәтижелердің алғашқысы сутегі атомындағы электронның импульс моментінің квантталуы

, (13.4)

мұндағы l= 0,1,2,...(n-1) − орбиталық кванттық сан деп аталады. (13.3) теңдеуінен шығатын келесі маңызды нәтиже электронның толық энергиясы квантталады және оның мәндері

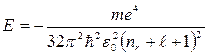(13.5)

өрнегімен анықталады, мұндағы n_r-радиалды кванттық сан.

Бор теориясынан алынған сутегі атомындағы электронның толық энергиясына арналған өрнек:

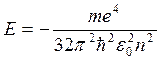, (13.6)

(мұндағы n=1,2,3,..., бас кванттық сан). Бұл өрнекті (12.5) теңдеуімен салыстырсақ, онда болады.

Сутегі атомындағы электронның энергетикалық деңгейлері тек ғана бас кванттық санға (n) тәуелді болады. (13.6) теңдеуден берілген n-ге сәйкес келетін l -дің үлкен мәніне l_max =n-1 (n_r=0 болғанда). Сондықтан, n-нің берілген мәні үшін орбиталық кванттық сан келесі мәндерді қабылдайды:

. (13.7)

Орбиталық кванттық санның әртүрлі мәндеріне сәйкес келетін электрон күйлерін келесі түрде белгілеу қабылданған:

l = 0 – S- күйі,

l = 1 – р- күйі,

l = 2 – d- күйі,

және т.б. (реті бойынша латын алфавитінің әріптерімен белгіленеді).

Спин векторы кеңістікте бар болғаны екі бағдарды қабылдауы мүмкін. Орбиталық импульс моменті сияқты

(13.8)

қатысын жазуға болады, мұндағы m_s=±1/2 спиндік магниттік кванттық сан деп аталады. Сонымен, атомдағы электрон күйі төрт кванттық сандармен анықталады, олар: n− бас кванттық сан, l − орбиталық кванттық сан, m _l − орбиталық магниттік кванттық сан, m_S − спиндік магниттік кванттық сан.

Үйлесімді сандардың айырылмайтындығы туралы квантты-механикалық ережені пайдаланып, В. Паули мынадай принципті тағайындады: кез-келген атомның стационар күйлерінде n, l, m_l және m_S төрт кванттық сандары бірдей екі электронның болуы мүмкін емес. Паули принципіне сәйкес, бірдей төрт кванттық сандар жиынында тұрған электрондардың Z(n, l, m _l, m_S) саныZ₁(n, l, m _l,m_s)=0 немесе 1 болады.Бірдей үш кванттық сандар жиынындағы электрондар саны Z₂(n, l, m _l)=2 болады. яғни m_s-тек +1/2 және -1/2 екі мәнді қабылдауы мүмкін.

Бірдей екі кванттық сандар n және l күйлерінде тұрған электрондардың максимум саны

Z₃(n,l) = 2(2l+1).

Соңғы теңдеуді l =0 ден l =n-1 -ге дейінгі мәндер бойынша қоссақ, онда бас кванттық санмен n анықталатын күйлерде тұрған электрондар саны:

. (13.9)

13.1-кестеде n − бас және l − орбиталық кванттық сандардың берілген мәндерімен сипатталатын күйлердегі электрондардың максимум саны көрсетілген.

13.1-кесте

n	Қабат	Күйлердегі электрондардың саны	Электрондардың максимум (max) саны
s (l =0)	p (l =0)	d (l =2)	f (l =3)	g (l =4)
...	K L M N		-	- -	- - -	- - - -

Осы кезге дейін біз сутегі атомындағы электронның қозғалысын қарастырдық. Бірақ Менделеев кестесіндегі келесі атом үшін, мәселен екі электроны бар гелий үшін Шредингер теңдеуінің шешілуі қиындайды. Бірақ, Менделеев кестесінің бірінші тобындағы элементтер сілтілік металдар атомының ішкі қабаты электронмен толтырылған, ал сыртқы қабатында бір электрон болғандықтан есепті оңайлатуға болады. Бұл жағдайда атомды жалпы заряды ядроның заряды +Ze мен оны қорашаған ішкі қабаттарда орналасқан электрондардың зарядынан -(Z-1)e тұратын атомдық қалдыққа және осы жасалған қалдықтың өрісінде қозғалатын электронға (валенттік электрон) бөліп қарастыруға болады.

Бұл кезде жүйе нүктелік заряд пен дипольден құралады деп алып, атом қалдығы валенттік электронға әсер етеді деп есептеуге болады. Жүйе орталығы нүктелік зарядпен дәл келеді, ал ось валенттік электрон арқылы өтеді деп есептеп, сілтілі атомдардың термдерін мына түрде беруге болады

, (13.10)

мұндағы R – Ридберг тұрақтысы, n – бас кванттық сан, s – орбиталық кванттық санға l тәуелді түзету.

Ядролар арасындағы потенциялық энергияны есептемегенде, сутегі атомының иондалған молекуласы үшінШредингер теңдеуі

(13.11)

түрде жазылады.

Берілген Шредингер теңдеуінің шешімі оқылатын курстан тыс, сондықтан бұл шешімнің нәтижелерін ғана пайдаланамыз. Сутегінің иондалған молекуласындағы электрон энергиясы мына түрде жазылады:

. (13.12)

интегралы жабу интегралы деп аталады. Ол y_А және y_В толқындық функцияларының бірін-бірі жабуын (көлеңкелеуін) сипаттайды. Е_А – иондалған сутегі молекуласының электроны мен ядроларының арасындағы кулондық әсерді сипаттайтын тұйықталған атомның негізгі күй энергиясы деп аталады, А – алмасу интегралы деп аталады, ол сутегінің иондалған молекулаласындағы А және В ядросы үшін электронның ажырамауына байланысты өзара алмасуы әсерін сипаттайды. Егер молекуладағы екі атом қатаң байланысқан деп есептесек, онда мұндай молекуланың айналуын инерция моменті J₀ және массасы молекуланың келтірілген массасына тең болатын бөлшектің айналуы ретінде қарастыруға болады. Мұндай бөлшектің импульс моменті келесі өрнек бойынша квантталады:

_, (13.13)

мұндағы j=0,1,2,… − айналу кванттық саны.

Берілген айналу деңгейдің энергиясы айналмалы кванттық санға байланысты, ол мына қатынаспен анықталады:

, (13.14)

мұндағы (Дж) – молекуланың айналу тұрақтысы. Сәулеленуге байланысты көшулер, көрші айналу энергия деңгейлерінің араларында ғана өтеді, яғни сұрыптау ережесіне бағынады D j =±1. Екі атомды молекуладағы атомдардың ядролары оның тепе-теңдік айналасында тербелмелі қозғалыс жасайды. Мұндай осциллятордың энергиясы келесі өрнек бойынша квантталады:

, (13.15)

мұндағы n₀ – осциллятор тербелісінің меншікті жиілігі, u=0,1,2,3... – тербелмелі кванттық сан. Тербелмелі энергиялық спектр тербелмелі энергиялық деңгейлер арасындағы көшу есебінен құралады және ол үшін сұрыптау ережесі Du=±1 орындалады.

Өзін-өзі бақылауға арналған тесттер:

1. Энергиясы E = 9 эВ электрондар үшін биіктігі U = 10 эВ және ені d = 5∙10 м тікбұрышты потенциалдық бөгеттің өткізу коэффициентін анықтау керек.

A)5,9 ∙ 10^-13

B)5,9 ∙ 10^-8

C)5,9 ∙ 10^-5

D) 5,9 ∙ 10^-3

E) 5,9 ∙ 10^-1

2. Бөлшек ені l бірөлшемді потенциалдық жәшік ішінде қозған күйде (n = 3) тұр. 0 < x < l аралығындағы қандай нүктелерде бөлшектің табылу ықтималдығының тығыздығы экстремалдық мәндерге ие болады?

A) х ₁ = l / 6, х ₃ = l / 2, х ₅ = 5 l / 16 кезінде максимал мән; х ₂ = l / 3, х ₄ = 2 l / 3 минимал мән

B) х ₁ = 5 l / 6, х ₃ = l / 2, х ₅ = 5 l / 6 кезінде максимал мән; х ₂ = 2 l / 3, х ₄ = 2 l / 3 минимал мән

C) х ₁ = l / 6, х ₃ = l / 2, х ₅ = 5 l / 6 кезінде максимал мән; х ₂ = l / 3, х ₄ = 2 l / 3 минимал мән

D) х ₁ = l / 6, х ₃ = l / 12, х ₅ = 5 l / 6 кезінде максимал мән; х ₂ = l / 3, х ₄ = 2 l / 5 минимал мән

E) х ₁ = l / 6, х ₃ = 3 l / 2, х ₅ = 5 l / 6 кезінде максимал мән; х ₂ = l / 3, х ₄ = 2 l / 13 минимал мән

3. Электрон ені l бір өлшемді шексіз терең потенциалдық «шұңқырда» орналасқан. l – дің: 1) 10 см; 2) 1 нм мәндері үшін екі көршілес энергетикалық деңгейлердің ең кіші айырымын есептеу керек.

A) 1) 3,1∙ 10^-16 эВ; 2) 2,1 эВ

B) 1) 2,1∙ 10^-16 эВ; 2) 3,1 эВ

C) 1) 0,1∙ 10^-16 эВ; 2) 0,1 эВ

D) 1) 1,1∙ 10^-16 эВ; 2) 1,1 эВ

E) 1) 5,1∙ 10^-16 эВ; 2) 4,1 эВ

4. Энергиясы Е = 25,0 эВ электрондар шоғы өз жолында биіктігі U = 9,0 эВ потенциалдық бөгетке кездеседі. Берілген бөгет үшін де Бройль толқынының R шағылдыру коэфициентін және D өткізу коэфициентін анықтау керек.

A) 1 /81; R + D = 1; D = 80 /81

B) 3 /81; R + D = 1; D = 78 /81

C) 4/81; R + D = 1; D = 77 /81

D) 5 /81; R + D = 1; D = 76 /81

E) 6 /81; R + D = 1; D = 75 /81

5. Бөлшек қабырғалары абсолют өткізбейтін ені l бірөлшемді (0 ˂ x ˂ l) тікбұрышты потенцалдық шұңқырда негізгі күйде орналасқан. Бөлшектің l / 3 ˂ x ˂ 2 l / 3 аймағында болу ықтималдығын табу керек.

A)4,61

B)3,61

C)2,61

D)1,61

E) 0,61

14-дәріс

Атом ядросы. Атом ядросының құрылысы.

Ядролық күштер. Ядролық күштердің ауыспалы сипаты.

Дата добавления: 2017-01-14