
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тура жол алгоритмі 4 страница
|
|
|
|
6.М1 матрицасына 2-5-ші пункттерді қайталап қолдану арқылы М2 матрицасын аламыз.
7. Осы процессті бір белгісізді бір жолдан тұратын теңдеу қалғанша жалғастырамыз.
8. Тастап кеткен басшы жолдардан жаңа жүйе құрастырамыз.
2. Кері жол алгоритмі
Басшы жолдардан құралған матрицаны әлдебір ауыстырулар арқылы үшбұрышты түрге келтіріп, ең соңғы теңдеуден ең соңғы белгісізді, оны қолданып оның алдындағы белгісізді, т.с.с. барлық белгісіздерді кері бағытта анықтаймыз.
 сандары қаншалықты азайған сайын есептеу қателігі де азаяды. Сондықтан ЭЕМ-ді қолданып есептеу уақытында осы әдіс тиімді деп есептеледі.
сандары қаншалықты азайған сайын есептеу қателігі де азаяды. Сондықтан ЭЕМ-ді қолданып есептеу уақытында осы әдіс тиімді деп есептеледі.
Ескерту. Егер жүйе өте көп белгісіздерден тұрып, оның барлық элементтерінің арасынан модулі бойынша үлкен элементті табу қиынға соқса басшы жол ретінде жүйенің бірінші жолын, ал басшы элемент ретінде осы жолдың модулі бойынша ең үлкен элементін алуға болады.
3. Квадрат түбірлер әдісі.
 (2.3.1)
(2.3.1)
Жүйенің матрицасы симметриялы элементтерден тұратын болса, онда мұндай жүйеге квадрат түбірлер әдісі қолданылады. Әдістің мақсаты ([13] қараңыз) берілген матрицаны бір-біріне түйіндес екі үшбұрыш матрицаның көбейтіндісі түріне келтірейік.
A=S*DS (2.3.2)
мұндағы S*- төменгі үшбұрышты матрица, S- жоғарғы үшбұрышты матрица.
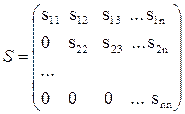
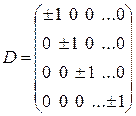
SS*D матрицасын бір-біріне көбейтіп элементтерін А матрицасының элементтеріне теңестіреміз. Алынған матрицасының диоганалдық элементтері мына формуламен есептелінеді.
|
|
|

ал қалған элементтер үшін мына формула қолданылады:


 (2.3.3)
(2.3.3)
 (2.3.4)
(2.3.4)
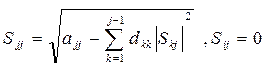 (2.3.5)
(2.3.5)
 (2.3.6)
(2.3.6)
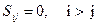 (2.3.7)
(2.3.7)
Егер берілген матрицаның коэффициенті нақты және бас минорлары оң болса, онда d матрицасын бірлік матрица деп, есептеу мына фолмулалармен жүргізіледі:
 (2.3.3*)
(2.3.3*)
 (2.3.4*)
(2.3.4*)
 (2.3.5*)
(2.3.5*)
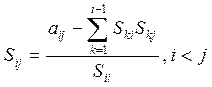 (2.3.6*)
(2.3.6*)
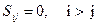 (2.3.7*)
(2.3.7*)
Бұл формулаларды қолданғаннан кейін шыққан матрицаны мынадай үшбұрышты жүйе құрамыз:
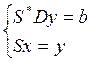 (2.3. 8)
(2.3. 8)
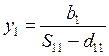 (2.3.9)
(2.3.9)
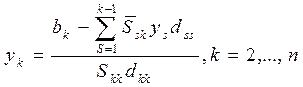 (2.3.10)
(2.3.10)
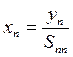 (2.3.11)
(2.3.11)

 (2.3.12)
(2.3.12)
4.Қарапайым итерация әдісі.
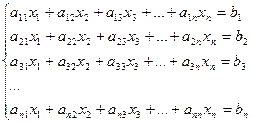 (1)
(1)
(1)- жүйені қандай да бір амалдар қолданып келесі түрге келтірейік,
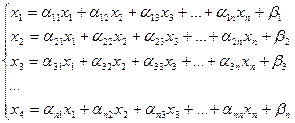 (1.1)
(1.1)
немесе қысқаша жазсақ: 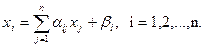
(1.1.) – жүйенің оң жағы n - өлшемді векторлық кеңістікте x(x1,x2,…,xn) нүктесін осы кеңістіктің y(y1,y2,…,yn) нүктесіне айналдыратын бейнелеу болып табылады:
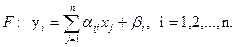 (1.2.)
(1.2.)
(1.1.) – жүйені қолданып, бастапқы 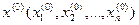 нүктені таңдап алып n - өлшемді векторлық кеңістікте нүктелердің итерациялық тізбегін құруға болады:
нүктені таңдап алып n - өлшемді векторлық кеңістікте нүктелердің итерациялық тізбегін құруға болады:
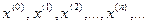 (1.3.)
(1.3.)
(1.3.) – итерациялық тізбек жинақты болса, оның шегі (1.1.) итерациялық жүйенің шешімі болады. Тізбектің жинақтылығын дәлелдеу үшін функционалдық анализдің кейбір ұғымдары керек:
5. Зейдель әдісі.
1. – жүйе (1.1.) – итерациялық түрге келтірілсін. Бұл жүйені қарапайым итерация әдісімен шешкенде итерациялық процесстің әр қадамы белгілі бастапқы жуықтаудан белгісіздің жаңа жуықтауына көшуден тұратын еді. Белгілі бастапқы жуықтаудың элементтерін x1, x2, …, xn деп, ал есептелетін келесі жуықтауларды y1, y2, …, yn деп белгілейік. Сонда есептеу формулалары келесі түрге көшеді:
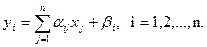 (2.1.)
(2.1.)
Зейдель әдісінің негізгі идеясы итерациялық процестің әр қадамында yi-дің мәндерін есептеу барысында оның алдында есептелген y1, y2, …, yi-1 мәндері қолданылады да (2.1.)– ді ашып жазсақ, Зейдель формуласы келесідей болады:
|
|
|
 (2.2.)
(2.2.)
(2.2.)– итерациялық процесінің жинақтылығы үш метрикалық кеңістікте мына шарттардың бірі орындалуымен бекітіледі:
1.  кеңістікте
кеңістікте 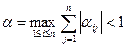 шарты (2.3.)
шарты (2.3.)
2. 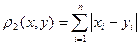 кеңістікте
кеңістікте  шарты (2.4.)
шарты (2.4.)
3. 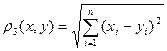 кеңістікте
кеңістікте 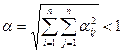 шарты. (2.5.)
шарты. (2.5.)
Егер бұл шарттардың біреуі орындалса, (2.2.)– итерациялық процесс кез келген бастапқы жуықтауда өзінің жалғыз шешіміне жинақталады.
Зейдель әдісін жүйенің матрицасы симметриялы элементтерден тұрған жағдайда қолданады. Егер матрица симметриялы болмаса оны симметриялы түрге келтіру үшін жүйенің матрицасын және векторларын транспонирленген матрицаға көбейтеді:
АТ*А*х=AT*b (2.6.)
Белгілеулер енгіземіз:
AT*A=C
AT*b=D
Сонда
Cx=D (2.7.)
(2.7.) – жүйені қалыпты жүйе деп атайды. Қалыпты жүйенің элементтері симметриялы және диагональды элементтері нөлден өзгеше болады. Қалыпты жүйені алдында қарастырған амалдарды қолданып (2.2.)– итерациялық жүйеге келтіруге болады.
(2.7.) – қалыпты жүйеге эквивалентті (2.2.)– келтірілген итерациялық жүйе үшін Зейдельдің итерациялық процесі өзінің жалғыз шешіміне кез келген бастапқы жуықтауларда жинақталады.
Егер е дәлдік берілсе, итерациялық әдіс 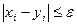 , i=0,1,2,… шарты орындалғанға дейін жалғасады.
, i=0,1,2,… шарты орындалғанға дейін жалғасады.
5-ДӘРІС. Матрицаның меншікті мәндері мен меншікті векторлары.
1. Матрицаның меншікті мәндері мен векторларын табу.
2. Крылов әдісі.
3. Меншікті мәндердің дербес мәселелері.
4. Дәрежелеу әдісі.
5. Симметриялық матрицаның меншікті мәндері мен векторлары.
6. Якобидың айналдыру әдісі.
6-ДӘРІС. Бейсызықты теңдеулер жүйесінің шешімін табу.
1. Жай итерация әдісі.
2. Ньютон-Гаусс әдісі.
3. Ньютон әдісінің жинақталуы.
7-ДӘРІС. Функцияны жуықтау.
1. Интерполяцияесебініңқойылуы.
2. Лагранж формуласы.
3. Лагранж формуласының жалқылығы және қателігін бағалау.
4. Бір айнымалы функцияны кубтық сплайнмен интерполяциялау.
5. Сплайн функциясының жинақталуы.
Дәріс тезисі
F(x) функциясының белгілі мәндері келесі таблицаны құрсын.
|
|
|
| X0 | X1 | … | xn | ||
| F(xi) | Y0 | Y1 | … | yn |
[x0, xn] аралығында жататын, бірақ xi-лердің ешқайсысымен сәйкес келмейтін х-тегі функция мәнін табу керек болсын.
Әдетте функцияның аналитикалық өрнегі берілсе, онда х-тің орнына мәнін қойып функция мәнін есептей салуға болатын. Кей жағдайда функцияның аналитикалық өрнегі мүлде белгісіз болуы немесе есептеуге көп уақытты қажет етуі мүмкін. Осындай жағдайларда берілген таблица бойынша f функциясына жуық F жуықтаушы функцияны құрады:
f(x)=F(x) (2)
Құрылған жуықтаушы функция келесі шарттарды қанағаттандыруы керек:
F(x0)=y0, F(x1)=y1, F(x2)=y2, …., F(xn)=yn (3)
Мұндай есепті функцияны интерполяциялау есебі деп атайды. Ал х0, x1, x2, …, xn нүктелерін – интерполяциялау тораптары немесе түйіндері деп атайды.
F(x) интерполяиялаушы функцияны n дәрежелі көпмүшелік түрінде іздейді: Лагранж, Ньютон, Гаусс, Бессель, Стирлинг, т.б.
Егер интерполяциялық түйіндердің бір бірінен ара қашықтықтары тұрақты емес болса, Лагранждың көпмүшелігі, тұрақты болса – Ньютоннның көпмүшеліктері қолданылады.
1. Лагранждың интерполяциялық көпмүшелігі.
 (1)
(1)
Кей жағдайда есептеу процесін жеңілдету үшін x=at+b, xj=atj+b j=0,1,…,n сызықты алмастыруын жасау арқылы Лагранж коэффициенттерінің инварианттылығын қолдануға болады, онда (1)-формула келесі түрге келеді:
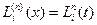 (2)
(2)
2. Ньютоннның интерполяциялық формулалары.
Егер интерполяциялық түйіндердің бір бірінен ара қашықтығы тұрақты болса, практикада Ньютонның интерполяциялық формулалары қолданылады. Бұл формулалар екіге бөлінеді:
- Алдыға қарай интерполяциялау
- Кері интерполяциялау
Егер берілген х нүктесінің мәні таблицаның бас жағында жатса, 1-формуласы қолданылады:
|
 .
.
Мұндағы 
Егер берілген х нүктесінің мәні таблицаның соңғы жағянда жатса, 2-формула қолданылады:
|
|
|
|


Формулалардағы 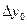 ,
, 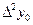 , т.с. сияқтылар шектік айырымдар деп аталады және 3-таблицаны толтыру арқылы анықталады. Таблицада мысал үшін 6 интерполяциялық түйін және шектік айырымдардың 4-ші дәрежесіне дейінгі мәндер қарастырылған. 1-формула үшін таблицаның бірінші жолындағы мәндер, 2-формула үшін таблицаның соңғы жолындағы мәндер қолданылады.
, т.с. сияқтылар шектік айырымдар деп аталады және 3-таблицаны толтыру арқылы анықталады. Таблицада мысал үшін 6 интерполяциялық түйін және шектік айырымдардың 4-ші дәрежесіне дейінгі мәндер қарастырылған. 1-формула үшін таблицаның бірінші жолындағы мәндер, 2-формула үшін таблицаның соңғы жолындағы мәндер қолданылады.
3-таблица. Шектік айырымдар таблицасы.
| X | y | 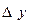
| 
| 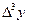
| 
|
| X0 | Y0 | 
| 
| 
| 
|
| X1 | Y1 | 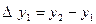
| 
| 
| 
|
| X2 | Y2 | 
| 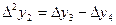
| 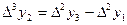
| |
| X3 | Y3 | 
| 
| ||
| X4 | Y4 | 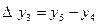
| |||
| X5 | Y5 |
Егер интерполяциялық түйіндер саны 1 немесе 2-ге тең болса сызықты интерполяциялық формуланы қолдануға болады:  .
.
Қателіктерін бағалау:
1-формула үшін мына формула қолданылады:
 ,
, 
немесе 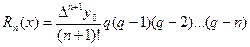

2-формула үшін мына формула қолданылады:
 ,
, 
1. Эйткен схемасы
2. Гаусс интерполяциялық формулалары
3. Стирлингтің және Бессельдің интерполяциялық көпмүшеліктері
Эйткен схемасы
Егер Лагранж көпмүшелігінің жалпы өрнегін анықтамай, тек белгілі бір нүктедегі функция мәнін есептеу керек болса, онда Эйткен схемасын қолдануға болады:


 т.с.с. (4.6)
т.с.с. (4.6)
Эйткен схемасы келесі 6-кестені толтыру арқылы орындалады.
6-кесте. Эйткен схемасының толтырылу кестесі
| xi | yi | Xi-x | Li-1,i | Li-2,i-1,i | Li-3,i-2,i-1,i | … |
| X0 | Y0 | X0-x | ||||
| X1 | Y1 | X1-x | L01(x) | |||
| X2 | Y2 | X2-x | L12(x) | L012(x) | ||
| X3 | Y3 | X3-x | L23(x) | L123(x) | L0123(x) | … |
| X4 | Y4 | X4-x | L34(x) | L234(x) | L1234(x) | … |
Эйткен схемасын есептеуді көршілес L0123…n(x), L0123…n,n+1(x) мәндері берілген дәлдік маңайында бір бірімен беттессе тоқтатуға болады.
Xi нүктелерінде yi мәндерін қабылдайтын n-ші дәрежелі интерполяциялық көпмүшелік келсі түрде де жазылады:
 . (4.7)
. (4.7)
1-Мысал:
Төмендегі кестемен берілген функция үшін Лагранж көпмүшелігін құру.
| I |
| |||||
| xi | 0.1 | 0.3 | 0.5 | |||
| yi | -0.5 | 0.2 |
Шешімі: (4.4)-формула бойынша n=3, i=0,1,2,3 болғандағы өрнекті анықтаймыз:
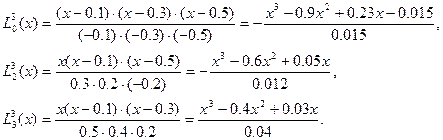
L13(x) мүшесін есептемейміз, себебі y1=0. Бәрін бір біріне қосамыз да көпмүшеліктің соңғы түрін аламыз:
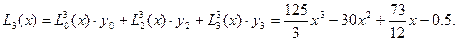
2-мысал:
Төмендегі кестемен берілген функцияның x=0.45 нүктесіндегі мәнін анықтау керек.
| X | 0.05 | 0.15 | 0.20 | 0.25 | 0.35 | 0.40 | 0.50 |
| ||
| y | 0.9512 | 0.8607 | 0.8187 | 0.7788 | 0.7047 | 0.6703 | 0.6065 | 0.5769 |
Шешімі:
Есептеуді жеңілдету үшін x=0.05t деп алайық. X-тердің мәні белгілі болғанда t-лардың мәндерін тауып алуға болады, олар: 1, 3, 4, 5, 7, 8, 10, 11. Және x=0.45 болғандағы t=9 болады. Есептеу қадамдары 6’-кестеде келтірілген.
6’-кесте. (4.9)-есептің есептелу қадамдары.
| I | ti-tj (i<>j) | Di | yi |

| |||||||||
| -2 | -3 | -4 | -6 | -7 | -8 | -10 | -725 760 | 0.9512 | -0.0131*10-4 | ||||
| -1 | -2 | -4 | -5 | -7 | -8 | 26 880 | 0.8607 | 0.3202*10-4 | |||||
| -1 | -3 | -4 | -6 | -7 | -7 560 | 0.8187 | -1.0829*10-4 | ||||||
| -2 | -3 | -5 | -6 | 5 760 | 0.7788 | 1.3520*10-4 | |||||||
| -1 | -3 | -4 | -3 456 | 0.7047 | -2.0390*10-4 | ||||||||
| -2 | -3 | 2 520 | 0.6703 | 2.6599*10-4 | |||||||||
| -1 | -1 | 11 340 | 0.6065 | 0.5348*10-4 | |||||||||
| -2 | -80 640 | 0.5769 | -0.0715*10-4 | ||||||||||

| 
| ||||||||||||
Сонымен y(0.45)= 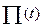
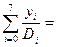
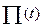
 3840*1.6604*10-4=0.6376.
3840*1.6604*10-4=0.6376.
Егер есепте керісінше функция мәні белгілі болып сол мәнге сәйкес абсцисса мәнін табу керек болса, ондай есепті кері интерполяциялау деп атайды. Кері интерполяциялау формуласы:
|

Гаусс интерполяциялық формулалары
Гаусс формулаларын берілген х-тің мәні кестенің ортасына жақын орналасқан жағдайларда қолданады. Егер x>x0 болса Гаусстың 1-формуласы, x<x0 болса, Гаусстың 2-формуласын қолданады.
1-формуласы:
|

2-формуласы:
|
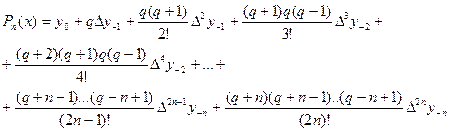
Бұл формулалардағы  ,
, 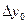 ,
, 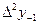 ,
,  ,
, 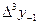 ,
, 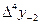 ,
, 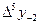 ,
, 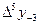 ,
,  шектік айырымдарды табу үшін 9- кесте құру керек.
шектік айырымдарды табу үшін 9- кесте құру керек.
9 - кесте. Гаусс формуласы үшін шектік айырымдар кестесі.
| x | Y | 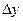
| 
| 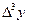
| 
| 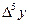
| 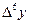
|
| x-4 | y-4 | 
| |||||
| x-3 | y-3 | 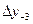
| 
| 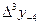
| 
| 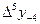
| 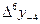
|
| x-2 | y-2 | 
| 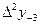
| 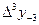
| 
| 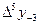
| 
|
| x-1 | y-1 | 
| 
| 
| 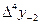
| 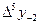
| 
|
| X0 | Y0 | 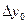
| 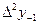
| 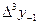
| 
| 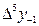
| |
| X1 | Y1 | 
| 
| 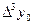
| 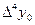
| ||
| X2 | Y2 | 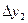
| 
| 
| |||
| X3 | Y3 | 
| 
| ||||
| X4 | Y4 |
Мысалы:
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 1748; Нарушение авторских прав?; Мы поможем в написании вашей работы!