Тура жол алгоритмі 6 страница

(6.11)

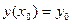(6.12)

(6.11)-теңдеу екі өлшемді қарапайым дифференциалдық теңдеу (ҚДТ) және (6.12)-бастапқы шарт берілсін. [x₀, x_n] аралығында у-тің мәндерін анықтап, функция графигін сызу керек болсын. Бұл есепті шешудің көпқадамды әдістері: Адамс және Милн әдістері деп аталады.

Адамс әдісі

Адамс әдісінің идеясы бірқадамды әдіспен табылған мәндер кесте сын толықтыру немесе жалғастыру. Сондықтан есептеің берілгенінде бастапқы шартпен бірге бірнеше нүктедегі функция мәндері табылған болады.

Бастапқы шартты пайдаланып, функция өсімшесінің мәндерін анықтаймыз, оларды q_i (i=0,1,2,3) деп белгілейік:

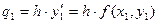
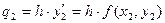
Енді осы мәндердің шектік айырымдарын табамыз:

,

Енді функцияның мәндерін есептеу үшін Адамс формуласын қолданамыз. Ол екі түрлі:

1 Экстраполяциялық формула:

,

, (6.13)

Бұл формуламен табылған 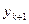мәндерін алдын ала анықталған функция мәндері деп атаймыз және , деп белгілейміз. (6.13)-формуламен табылған мәндерді тереңірек анықтау үшін интерполяциялық формуланы қолданамыз.

2 Интерполяциялық формула:

,

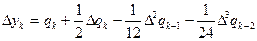, (6.14)

Бұл формуламен табылған мәндерін жөнделген немесе түзетілген функция мәндері деп атаймыз және , деп белгілейміз. Сосын (6.13) және (6.14)-формулалармен алынған мәндерді бір бірімен салыстырамыз. Егер төмендегі шарт орындалса:

онда әдіс өзінің жалғыз шешіміне жинақталады, орындалмаса – қадамды кішірейтіп есептеуді қайта жүргізу керек.

Практикада есептеуді жеілдету үшін Адамстың басқа формулалары да қолданылады:

1-формуласы: ), 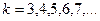(6.15)

2-формуласы: ), 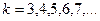(6.16)

Адамс әдісі дифференциалдық теңдеулер жүйесіне де қолданылады:

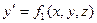
жүйесі берілсе, оған қолданылатын Адамс формулалары төмендегідей болады:

(6.17)

(6.18)

Мұндағы: ,

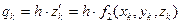
Милн әдісі

Бұл әдіс те Адамс әдісі сияқты мәндер кесте сын жалғастыруға мүмкіндік береді. Теңдеу, бастапқы шарт, және қандай да бір әдіспен табылған функцияның бірнеше мәндері берілсін. Функцияның қалған мәндерін анықтау керек.

(6.19)

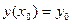(6.20)

,

мәндерді анықтау үшін Милн формулаларын қолданамыз:

1 Алдын ала анықтау: ,

2 Осы мәндерді қолданып

3 Милннің 2-ші формуласымен алдында табылған мәндерді түзетеміз немесе дәлдейміз: .

4 Табылған мәндердің қателігін бағалаймыз: . Бұл формула есептеудің әр қадамында алынған мәннің дәлдігін тексеріп отырады. Егер дәлдік берілсе және болса, онда деп алып y_i+1-лерді есептеуге болады, кері жағдайда қадамды кішірейту керек.

5 Милн әдісін жүйені шешуге де қолдануға болады. Егер жоғарғы ретті теңдеу берілсе оны 1-ші ретті теңдеуге келтіру керек.

1-мысал:

Адамс әдісін қолданып теңдеуін шешу. Бастапқы шарты y(0)=-1

Шешімі:

(6.15)-(6.16)-формулаларды қолданып есептейік. Рунге-Кутта әдісімен алдын ала бірнеше мәндер табылған болсын.

X₁=0.1 y₁=-0.97528

X₂=0.2 y₂=-0.94978

X₃=0.3 y₃=-0.92154

Есептеу қадамдарын 18-кестеге жазуға болады.

Кестені толтыру ережесіне тоқталайық:

1,2- бағандарға белгілі мәндерді толтырамыз. 3-бағанда у_k-дің (k=0,1,2,3)

белгілі мәндерін толтырамыз. Осы мәндерді қолданып,

18-кесте. теңдеуін шешудің алгоритмі.

K	xk	yk	Y^`k
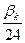
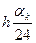
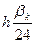
	0.0	-0	0.25
	0.1	-0.97528	0.24779
	0.2	-0.94978	0.26552
	0.3	-0.92154	0.30232	0.32834	0.32840	0.03283	0.03284
	0.4	-0.88871	0.35745	0.39237	0.39246	0.03924	0.03925
		-0.88870
	0.5	-0.84946	0.43040
		-0.84946

формуласымен 3-бағандағы сәйкес мәндерді анықтаймыз. 5-6 – бағандардағы белгілеулері (6.15)- (6.16)- формулалардағы жақша ішіндегі қосындыны білдіреді. K=3 болғанда мәнін 5-бағанның сәйкес жолына жазамыз. K=4 болғанда (6.15)-формуламен мәнін тауып, кестеде өз орнына жазамыз. Осы табылған х₄, у₄ мәндерін қолданып табамыз. 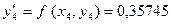мәнін есептеп өз орнына жазамыз. Әрі қарай K=3 болғанда 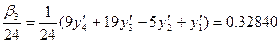мәнін есептеп өз орнына жазамыз. Енді табылған у₄ мәнін (6.16)- формуламен түзетеміз: . Табылған екі мән бір біріне өте жуық болғандықтан кестедегі алдыңғы табылған мәнін мәнімен түзетеміз. Осы әдіспен кестенің келесі жолын толтыруға болады.

Қарапайым дифференциалдық теңдеулер үшін шектік есептер. Ақырлы – айырымдық әдістер.

1. Ақырлы – айырымдық әдіс.

2. Қуалау әдісі.

F(x,y,y^’,y^’’)=0 (1)

2-ретті дифференциалдық теңдеу берілсін.

Біз осыған дейінгі есептерде Коши есебі деп дифференциалдық теңдеуге қосымша функцияның бір тәуелсіз айнымалыдағы мәні берілген жағдайды айтып жүрдік. Ал функцияның екі тәуелсіз айнымалыдағы мәндері берілсе, есепті ҚДТ үшін шектік есеп деп айтады. Қосымша шарттарды шекаралық шарттар дейді. Коши есебінде тәуелсіз айнымалы ретінде уақытты қарастырғанбыз, сонда есептің физикалық мағынасы серіппеге ілінген дененің еркін қозғалысын зерттеу болған. Ал шектік есепте тәуелсіз айнымалы ретінде ұзындық қарастырылады, яғни есептің физикалық мағынасы қатты серіппенің деформациясын зерттеу немесе, электр желілерін басқару, есептеу, химиялық реакциялардың нәтижелерін есептеу, снаряд қозғалысының теңдеуін құру сияқты практикада қарапайым классикалық әдістермен шешілмейтін «қатты» есептерді зерттеу болып табылады.

(1) теңдеу үшін екінүктелі шектік есеп келесідей қойлады: [a,b] аралығында (1) теңдеуін және осы аралықтың екі шеткі нүктелерінде

j₁[ y(a), y ^/ (a) ]=0 (2)

j₂[ y(b),y ^/(b) ]=0

шекаралық шарттарын қанағаттандыратын y=y(x) шешімін табу керек.

(1) теңдеу және (2)- шекаралық шарт сызықты болған жағдайды қарастырайық. Мұндай шектік есептер сызықты шектік есептер деп аталады және төмендегідей түрде жазылады:

y ^// +p(x) y ^/ + q(x) y = f(x) (3)

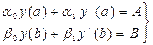(4)

мұндағы p(x), q(x), f(x) – функциялары [a,b] аралығында үзіліссіз функциялар, ал a₀,a₁,b₀,b₁, A,B –берілген тұрақтылар және ½a₀½+½a₁½¹0, ½b₀½½b₁½¹0.

Егер A=B=0 болса, онда (4) – шекаралық шарттар біртекті шекаралық шарттар деп аталады.

Қарапайым дифференциалдық теңдеулер үшін қойылған шектік есепті шешудің жалпы 2 әдісі бар:

1. Дифференциалдық теңдеудің ақырлы – айырымдық немесе шектік – айырымдық түрін қолдану – сандық әдіс.
2. Шектік есепті бірнеше Коши есебін шешуге келтіру аналитикалық әдіс.

1. Ақырлы – айырымдық әдіс.

Бұл әдістің негізгі идеясы - шектік есепті шешуді алгебралық теңдеулер жүйесін шешуге келтіру.

Берілген аралықты бірнеше бөлікке бөлу арқылы бірдей қашықтықта орналасқан түйіндер жүйесін құрамыз: x₀=a, x_n=b, x_i=x₀+ih (i=1,2,…,n-1), қадамы h=b-a/n және p_i=p(x_i), q_i=q(x_i), f_i=f(x_i) болсын.

x_i түйіндерінде ізделінді функцияның жуық мәнін y(x) және y ^/(x),y ^//(x) туындыларын сәйкесінше y_i ,y_i^/,y_i ^// деп белгілейік. Құрылған түйіндер жүйесінің әрбір ішкі түйінінде y_i^/(x_i), y_i^//(x_i) туындыларын сәйкес ақырлы – айырымдық қатынастарымен алмастырамыз:

(5)

Шекаралық шарттар үшін:

(5^!)

қатынастарын қолданылады.

(5) – қатынастарды (1) – ге қойсақ және шекаралық шарттарды ескерсек, сызықты алгебралық теңдеулер жүйесін немесе сызықты емес теңдеулер жүйесін аламыз. Бұл жерде (1)-теңдеудің сипатына көңіл аудару арқылы оның қандай жүйеге келетінін алдын ала анықтауға болады. Егер (1)-теңдеу сызықты болса, онда есеп сызықты алгебралық теңдеулер жүйесін шешуге келеді, ал сызықты емес болса, онда сызықты емес теңдеулер жуйесін шешуге кейде трансцендентті теңдеуді шешуге келеді.

Егер құрылған жүйені шешу қиынға соқса, онда шектік есепті екі Коши есебін шешуге келтіруге болады.

(3), (4)- шектік есепті қарастырайық. (4)-шекаралық шартта деп есептесек,

(6)

екенін көреміз. Мұндағы , 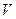- төмендегі түрге келтірілген Коши есептерінің шешімдері болады:

(7)

(8)

(7)-есептің шешімі 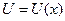, (8)-есептің шешімі , ал (6)-теңдеудегі с – тұрақты, белгісіз. Оны анықтау үшін (4)-шекаралық шартты ескереміз:

(9)

(7), (8) - шектік есептердегі туындыларды сәйкес айырымдық қатынастармен алмастырамыз:

бұдан келесі есепті аламыз:

(10)

және

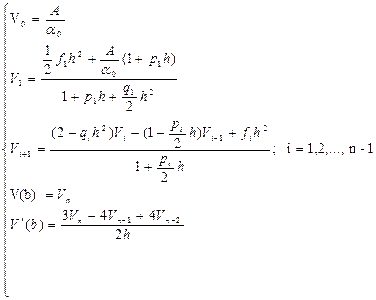(11)

(10)-(11)-жүйелерді шешіп болған соң (9)-формуламен с тұрақтысы табылса 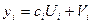теңдеуін шешу арқылы ізделінді мәндерді табуға болады.

Егер шекаралық шарттар түрінде берілсе, болады да есептеу формулалары жеңілдейді:

болады.

2. Қуалау әдісі.

(3)-(4)-шектік есептерді ақырлы-айырымдық қатынастармен алмастырған соң алынған есепті келесі түрде қарастырайық:

Мұндағы

m_i=-2+hp_i, k_i=1-hp_i+h²q_i (i=0,1,2,…,n-2) (16)

Сонда жүйе мынадай түрге келеді:

Y_i+1=c_i (d_i-y_i+2) (i=0,1,2,…,n-2) (17)

с_i,d_i сандары i=0 болғанда

(18)

i=1,2,…,n-2 болғанда біртіндеп

c_i=1/(m_i-k_ic_i-1) (19)

d_i=f_ih²-k_ic_i-1d_i-1

формулалармен есептеледі.

Есептеу этаптары:

Тура жол. (16)-формуламен m_i,k_i мәндерін табамыз. Сосын (18)-формуламен c₀, d₀ –дарды және (19)-формуламен i=1,2,…,n-2 үшін біртіндеп c_i, d_i мәндерін табамыз.

Кері жол. (17)-формуламен i=n-2 болғанда және (3)-(4)-теңдеулер жүйесінің соңғы теңдеуінен

Y_n-1=c_n-2(d_n-2-y_n)

екенін анықтаймыз. Бұл жүйені y_n бойынша шешеміз:

(20)

Алдын ала табылған c_n-2, d_n-2 мәндерін қолданып y_n мәнін табамыз. Сосын біртіндеп (i=n-1,…,1) үшін (17)- формуланы қолданып y_i мәндерін есептейміз:

(21)

Сосын y₀ мәнін (3)-(4)-теңдеулердің ең соңғысының алдындағы теңдеуінен табамыз:

(22)

Сонымен, барлық есептеулер екі рет қуаланып шығады. Тура жолда i индексінің өсу ретімен көмекші c_i, d_i сандары алынады. Бұл арада c₀, d₀ сандарын есептеу үшін интегралдау аралығының сол жақ шетіндегі шекаралық шарт қолданылады. Сосын кері жолдың алғашқы қадамында есептелген c_n-2, d_n-2 сандарының интегралдау аралығының оң жақ шетіндегі шекаралық шартпен үйлестірілуін қадағалайды. Осыдан барып I индексінің кему ретінмен біртіндеп y_i ізделінді мәндер есептеледі.

Математикалық физиканың теңдеулерінің сандық әдістері.

1. Екінші ретті КДТ үшін шеттік есептерге сандық әдістер.

2. Тор туралы түсінік. Торлық функция.

3. Біртекті баланс схемалары.

4. Марчук тепе-теңдігі.

Шектік есептерді шешудің вариациялық әдістері

1. Вариациялық есеп

2. Галеркин әдісі.

Дәріс тезисі:

Функционал және оператор. Функционалдық анализдің осы тақырыпқа қажетті ұғымдарын атап өткен дұрыс.

1-анықтама. К={g(x)}, мұндағы x – тәуелсіз айнымалы немесе бірнеше тәуелсіз айнымалылар жиыны х=(х₁,х₂, …,х_n) әлдебір функция класы немесе жиыны берілсін. I=I[g(x)] айнымалы шамасы g(x) функциясынан функционал (функциядан функция) деп айтады, егер әрбір g(x)ÎK функциясы үшін берілген ереже немесе заң бойынша I анықталған сан сәйкес қойылса.

Берілген функционал анықталған К={g(x)} функциялар класы функционалдың анықталу облысы немесе функционалдың берілу облысы деп аталады, ал функциялардың өздері мүмкін функциялар деп аталады.

1-мысал.

К={g(x)} функциялар класы – х=0 нүктесінде дифференциалданатын функциялар жиыны болсын. k=g^/(0) санын К облысында анықталған g(х) функциясының функционалы деп қарастыруға болады.

2-мысал.

[a, b] аралығында үзіліссіз дифференциалданатын, яғни g(x)ÎC⁽¹⁾[a, b] болатын g(х) функциясының К жиынын қарастырайық. x=a және x=b нүктелері арасындағы g=g(x) қисығының s доғасының ұзындығы K облысында g(x) функциясынан 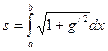формуласымен өрнектелетін функционалы болады.

3-мысал.

К – G облысында тұйықталған үзіліссіз және Г шекарасында нөлге айналатын барлық теріс емес z=f (x,y) функциялар жиыны болсын. көлемі f(x,y)-тен функционал болады.

2-анықтама. К функциялар жиыны сызықты деп аталады, егер әрбір uÎK және vÎK функциялары үшін u+vÎK қосындысы да осы жиында жатса, сонымен қатар auÎK (a- кез келген тұрақты) болса.

Полиномдар жиыны, барлық үзіліссіз функциялар жиыны, облыстың шекарасында нөлге айналатын функциялар жиыны сызықты функциялар жиыны бола алады.

3-анықтама. I=I[g] функционалы сызықты деп аталады, егер ол К сызықты функциялар облысында анықталған болса және кез келген мүмкін u, v функциялар жұбы үшін келесі қатынас ақиқат болса:

I[au+ bu]= aI[u]+ bI[v]

мұндағы a және b кез келген тұрақты.

k=g^/ (0) функционалы сызықты бола алады.

4-анықтама. К={g(x)} жиынында L операторы анықталған дейді, егер әрбір g(x)ÎK функциясы үшін әлдебір заң бойынша жалғыз ғана z=z(x) функциясы сәйкес қойылса. (Сонымен қатар, z(x) функциясы басқа t=(t₁, …, t_m айнымалыдан тәуелді болуы мүмкін).

Бұл функциялар арасындағы сәйкестік келесі түрде белгіленеді:

Z=Lg z=L(g)

берілген L операторы анықталған g=g(х) функциясының К жиыны бұл оператордың берілу облысы деп аталады, ал функциялар gÎК мүмкін функциялар деп аталады.

5-анықтама. L операторы сызықты деп аталады, егер ол сызықты жиында анықталған болса және кез келген мүмкін u және v функциялар жұбы үшін сызықты комбинациялары au +bv (a және b – еркін тұрақты) да мүмкін функциялар болып, сонымен қатар

1) L(au) = aLu;

2) L(u+v) = Lu+ Lv, шарттары орындалса.

Бұдан кез келген a және b үшін L(au + bv) = aLu +bLv екендігі шығады.

К - w облысында анықталған, нақты, үзіліссіз {u} функциялар жиыны болсын. Егер uÎK және vÎK болса, онда (u,v)= саны u және v функцияларының скаляр көбейтіндісі деп аталады және (u,v)=(v,u) болатыны сөзсіз.

6-анықтама. w облысында үзіліссіз берілген u сызықты функциялар жиынында L сызықты операторы анықталған болсын. Оның Lu мәндері де w облысында анықталған және үзіліссіз функциялар болады. Онда L сызықты операторы симметриялы деп аталады, егер кез келген мүмкін u және v функциялар үшін келесі қатынастар ақиқат болса:

яғни

(Lu,v)=(u,Lv). (7.38)

Егер кез келген мүмкін u функциясы үшін uº0 болғанда ғана (Lu, u) 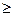0 теңсіздігі орындалса, онда L оператоы оң оператор деп аталады.

4-мысал.

gÎС⁽²⁾[0,1] функциялар жиынында анықталған Lg=-gⁿ операторын қарастырайық және g(0)=0, g^/(1)=0 болсын.

Егер u және v мүмкін функциялар болса, онда 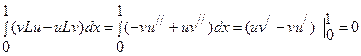болады, сондықтан

, яғни (Lu,v)=(u,Lv) болады және L операторы симметриялы деп есептеледі. Сонымен қатар uº0 екенін ескерсек, шекаралық шарттардың күші бойынша u≠0 болғанда

Дата добавления: 2017-01-14