Признаки сходимости числовых рядов c положительными членами

Числовой ряд называется рядом с положительными членами или просто положительным рядом, если все числа u₁, u₂, u₃,..., u_{n ³} 0. Рассмотрим некоторые достаточные признаки сходимости для положительных рядов.

1. Первый признак сравнения. Пусть даны три ряда:

-- ряд, сходимость которого надо определить,

u₁ + u₂ + u₃ +... + u_n +...; (7.6)

-- сходящийся ряд

v₁ + v₂ + v₃ +... + v_n +...; (7.7)

-- расходящийся ряд

w₁ + w₂ + w₃ +... + w_n +...; (7.8)

Тогда:

а) если начиная с некоторого номера n, выполняется условие

u_n £ v_n (7.9)

то из сходимости ряда (7.7) следует сходимость ряда (7.6);

б) если, начиная с некоторого номера n, выполняется условие

u_n ³ w_n (7.10)

то из расходимости ряда (7.8) следует расходимость ряда (7.6).

Доказательство

а).Обозначив частичные суммы

S_n = u₁ + u₂ + u₃ +... + u_n; Ф_n = v₁ + v₂ + v₃ +... + v_n;

в силу (7.9) имеем S_n £ Ф_n.

По условию задачи ряд (4.38) сходится, т.е. 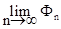= Ф, следовательно

Ф ³ Ф_n ³ S_n.

Это означает, что последовательность частичных сумм S_n возрастает (в силу положительности ряда) и ограниченна сверху величиной Ф. Поэтому 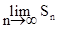существует и конечен, а ряд (7.6) сходится.

б). Обозначив

W_n = w₁ + w₂ + w₃ +... + w_n +...,

в силу (7.10) имеем S_n ³ W_n.

По условию ряд (7.8) расходится, т.е. 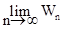= ¥, следовательно

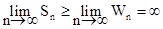
и ряд (7.6) расходится.

Второй признак сравнения. Пусть даны два ряда

u₁ + u₂ + u₃ +... + u_n +... (7.11)

v₁ + v₂ + v₃ +... + v_n +... (7.12)

и можно указать такие постоянные числа k₁ > 0 и k₂ > 0, что, начиная с некоторого достаточно большого n,

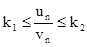(7.13)

Тогда ряды (7.11) и (7.12) одновременно сходятся или одновременно расходятся.

Доказательство. Из (7.13) следует, что

k₁ v_n £ u_n £ k₂ v_n. (7.14)

Если ряд (7.11) сходится, то из левого неравенства (7.12) согласно первому признаку сравнения вытекает сходимость ряда

k₁ v₁ + k₁ v₂ + k₁ v₃ +... + k₁ v_n +...

Из сходимости же этого ряда в соответствии со свойством 2 вытекает и сходимость ряда (7.12).

Предположим теперь, что ряд (7.11) расходится. В этом случае расходится и ряд

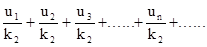
Из правой части (7.13) следует, что

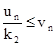
Следовательно, согласно первому признаку сравнения, ряд (7.12) также расходится.

Следствие (предельный признак сравнения). Если для рядов (7.11) и (7.12) выполняется условие

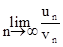= r < ¥, где r ¹ 0, (7.15)

то эти ряды сходятся или расходятся одновременно.

Доказательство. Соотношение (7.15) означает, что, начиная с некоторого n, все отношения вида u_n/v_n будут близки к r. Поэтому будут выполняться, например, неравенства

,

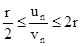откуда, согласно доказанной выше теореме, и вытекает данное следствие.

Для сравнения обычно используются следующие эталонные ряды.

Геометрический ряд

a + aq + aq² +... + aq^n-1 +....

Геометрический ряд сходится при условии q<1. В противоположном случае (q ³ 1) ряд расходится. Например, ряд

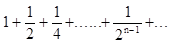
сходится (q = 1/2), а ряд

1 + 2 + 4 +... + 2^n-1 +...

расходится (q = 2). Можно также сказать, что этот ряд расходится потому, что не выполнено необходимое условие сходимости ряда.

Обобщенным гармоническим рядом называется ряд

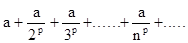
Этот ряд сходится при p > 1 и расходится при p £ 1.

Например, ряд

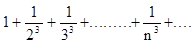- сходится, а ряд

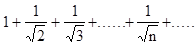- расходится.

Обобщенный гармонический ряд при p = 1 называют просто гармоническим рядом:

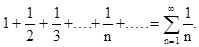
Гармонический ряд расходится!

Пример. Исследовать сходимость ряда

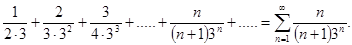
Решение. Сравним общий член этого ряда с геометрическим рядом 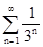, который сходится.

Так как

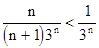
то, по первому признаку сравнения исследуемый ряд сходится.

Пример. Исследовать сходимость ряда

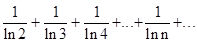
Решение. Сравнивая общий член этого ряда с общим членом гармонического ряда

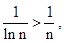
заключаем, что этот ряд также расходится (по первому признаку сравнения).

Пример. Исследовать сходимость ряда

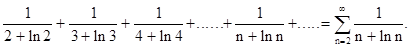
Решение. Воспользуемся следствием из второго признака сравнения, используя гармонический ряд

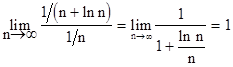
Сравниваемые ряды ведут себя одинаково, поэтому заключаем, что исследуемый ряд расходится (т.к. гармонический ряд расходится).

Пример. Исследовать сходимость ряда

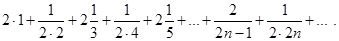
Решение. Рассмотрим отношение членов этого ряда к соответствующим членам гармонического ряда:

- при нечетном n имеем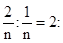

- при четном n имеем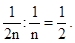

Следовательно, отношение u_n/v_n ни к какому пределу не стремится. Однако при всех n оно заключено между 1/2 и 2. Поэтому согласно второму признаку сравнения исследуемый ряд ведет себя так же, как и гармонический, т.е. расходится.

Признак Даламбера сходимости числовых рядов с положительными членами. Пусть дан положительный ряд

u₁ + u₂ + u₃ +... + u_n +.... (7.16)

Если отношения последующего члена ряда u_n к предыдущему u_n-1, начиная с некоторого значения n = N, удовлетворяет неравенству

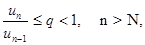(7.17)

то ряд (7.16) сходится.

Если же, начиная с некоторого N, имеем

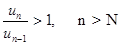(7.18)

то ряд (7.16) расходится.

Доказательство. Пусть имеет место соотношение (7.17), которое выполняется для всех n. Тогда

u_n £ u_n-1q, u_n-1 £ u_n-2q,..., u₂ £ u₁q.

Отсюда, подводя почленную подстановку, получаем

u_n £ u₁q^n-1

Это неравенство означает, что общий член ряда (7.16) не превосходит соответствующего члена сходящегося (q < 1) геометрического ряда. В силу первого признака сравнения ряд (7.16) сходится.

Пусть имеет место соотношение (7.18). Тогда

u₁ < u₂ < u₃ <...< u_n-1 < u_n <...,

т.е. члены ряда не убывают по мере возрастания n. Следовательно, не выполнено необходимое условие сходимости ряда и ряд (7.16) расходится.

На практике удобнее пользоваться предельным признаком Даламбера, формулировку которого дадим в виде следствия.

Следствие. (Предельный признак Даламбера). Если

,

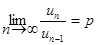то при p < 1 ряд (4.48) сходится, при p > 1 этот ряд расходится.

Пример. Исследовать сходимость ряда

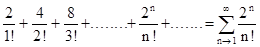
Решение. Рассмотрим предел отношения

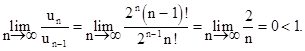
Следовательно, исследуемый ряд сходится.

Замечание. Если 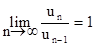, то признак Даnамбера не дает ответа на вопрос о сходимости ряда. В этих случаях надо привлекать другие признаки сходимости ряда.

Дата добавления: 2014-11-18