Постановка задачи Коши

Метод парабол (метод Симпсона)

Значительное повышение точности приближенных формул может быть достигнуто за счет повышения порядка интерполяции. Одним из таких методов приближенного интегрирования является метод парабол. Идея метода исходит из того, что на частичном промежутке дуга некоторой параболы в общем случае теснее прилегает к кривой y=f(x), чем хорда, соединяющая концы дуги этой кривой, и поэтому значения площадей соответствующих элементарных трапеций, ограниченных «сверху» дугами парабол, являются более близкими к значениям площадей соответствующих частичных криволинейных трапеций, ограниченных сверху дугой кривой y=f(x), чем значения площадей соответствующих прямолинейных трапеций. Сущность метода заключается в следующем. Отрезок [a,b] делится на 2n равных частей. Пусть точки деления будут

х₀=а, x₁, x₂, …x_2n-2, x_2n-1, x_2n=b,

а y₀, y₁, …y_2n – соответствующие значения подынтегральной функции на отрезке [a,b]. Произведем квадратичную интерполяцию данной подынтегральной функции на каждом из отрезков разбиения (заменим дугу графика подынтегральной функции дугой параболы с вертикальной осью) (рис. 11). Приведем без вывода формулу парабол в окончательном виде:

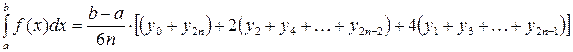. (7)

Подробный вывод формулы (7) см. в [13].

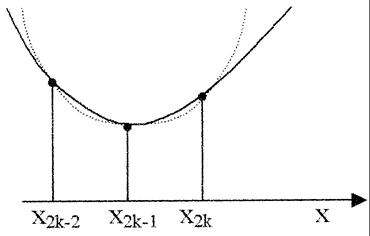
Рис. 11

Если подынтегральная функция f(x) имеет на отрезке [a,b] непрерывную четвертую производную, то для поправочного члена формулы (7) имеет место оценка

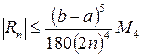, (8)

где М₄ - максимум модуля четвертой производной подынтегральной функции на отрезке [a,b].

Cравнивая между собой оценки (6) и (8), замечаем, что с увеличением n поправочный член формулы трапеций уменьшается пропорционально величине 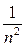, а для формулы парабол – пропорционально величине 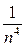, т.е. метод парабол сходится значительно быстрее метода трапеций, тогда как с точки зрения техники вычислений оба метода одинаковы.

ЛАБОРАТОРНАЯ РАБОТА №4

Задание: Вычислить интеграл по формулам левых и правых прямоугольников и по формуле трапеций при n=100. Сравнить полученные результаты со значением интеграла, вычисленным с помощью встроенных функций MathCad.

Образец выполнения задания

f(x):= 2×x задание подынтегральной функции

a:= 0 b:= 1 значения границ отрезка интегрирования

n:= 100 число точек разбиения отрезка

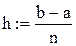величина h – длина отрезка разбиения

вычисление интеграла

i:= 0.. n

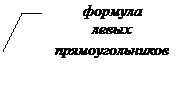x_i:= i×h y_i:= f(x _i)

k:= 0.. n - 1 p:= 1.. n

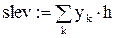
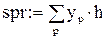
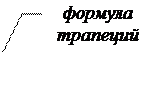slev = 0.99 spr = 1.01

t:= 0.. n - 1

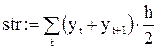
str = 1

Проверка полученного результата с помощью встроенных функций MathCad для вычисления определенного интеграла:

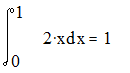
Глава 3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Решение большинства задач естествознания после соответствующих упрощений сводится к решению уравнений, содержащих искомую функцию или несколько функций, зависящих от одного или нескольких аргументов, сами эти аргументы и производные различных порядков от искомых функций, так называемых дифференциальных. Дифференциальное уравнение, полученное в результате исследования какого-либо реального процесса или явления, называют дифференциальной моделью этого явления или процесса. Мы будем рассматривать лишь модели, описываемые обыкновенными дифференциальными уравнениями, то есть уравнениями, в которых неизвестные функции зависят только от одной переменной.

Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида

y ¢= f (x, y). (1)

Решением дифференциального уравнения является некоторая функция y(x), которая при подстановке в выражение обращает его в тождество. Существует множество решений (так называемых частных решений) дифференциального уравнения (1), которые могут быть объединены и записаны в виде общего решения

y=y(x, C), (2)

где С – произвольная постоянная. Геометрически это можно интерпретировать как семейство интегральных кривых, каждая из которых является графиком решения (1) – рис. 12.

Для выбора одной кривой из семейства (частного решения y=y(x,c)) необходимо задать начальные условия

y(x₀)=y₀, (3)

то есть одну точку на искомой кривой решения.

Рис. 12

Как правило, практическое значение всегда имеет частное решение дифференциального уравнения. Задача нахождения частного решения уравнения (1), соответствующего начальным условиям (3), называется задачей Коши.

Дата добавления: 2014-12-16