Порядок построения математических моделей

Информационные модели

При исследовании физических и технологических процессов горного производства возникает необходимость установления закономерностей их протекания, т.е. выявления вида и параметров функций в ограничениях (6.2). Для этого используется широкий спектр математических методов:

- составление и решение уравнений механики сплошных сред, например, для изучения характера метановыделения из основных источников в шахтах;

- использование теории графов, например, для решения задач воздухораспределения в вентиляционных сетях;

- методы исследования операций и систем, например, для декомпозиции сложного технологического процесса на ряд простых;

- вероятностные методы (теория надежности, метод статистических испытаний и др.);

- методы теории адаптации, например, для приведения в параметрическое соответствие технологических систем добычи и переработки угля.

Целесообразность и условия применения того или иного метода существенно зависят от вида решаемой задачи.

Процесс построения математической модели включает в себя несколько этапов.

1.Вначале необходимо четко уяснить, что хочет получить исследователь. При построении оптимизационной модели - это означает выбор (вначале на качественном уровне) целевой функции. При построении информационной модели – это выяснение вида изучаемой закономерности (с определением ее размерности и качественным анализом влияющих факторов).

2.На втором этапе определяется, по возможности, наиболее полный комплекс факторов, влияющих на критерий или на характер протекания процесса.

3.Осуществляется переход от словесной к математической постановке задачи, т.е. формализации ее постановки.

4.Проводится анализ постановки задачи с целью изучения возможностей ее упрощения.

5.Выбирается метод решения задачи.

6.Осуществляется решение задачи для отдельных частных, наиболее характерных, случаев.

7.Производится логическая или экспериментальная проверка модели и полученного решения.

Данная схема не является универсальной, т.к. построение и решение модели требуют изобретательности. Это принципиальная схема, которая показывает порядок работ и в каждом конкретном случае, в зависимости от задачи исследования, может быть модифицирована. Однако, в общем случае ей следует руководствоваться.

Одним из важнейших является четвертый этап построения модели. После ее составления не следует торопиться с поиском метода решения, до конца не исчерпав возможностей упрощения. Практика исследований показывает, что грамотно вставленная и упрощенная модель - это 50 % успеха при ее решении.

При упрощении рекомендуется максимально (но в разумных пределах) снижать размерность решаемой задачи. Практика показывает, что снижение равномерности на одну переменную, на порядок упрощает возможность решения задачи. Для снижения размерности полезно пользоваться соображениями симметрии, а также делить задачу на 2-3 (например, рассматривая ее в разных плоскостях) и т.д.

После постановки задачи, особенно, если она представлена в виде системы дифференциальных уравнений, следует, по возможности, перейти к безразмерным параметрам (чтобы каждый член уравнения имел нулевую размерность). Это дает возможность выявить безразмерные физические комплексы, влияющие на решение т.е. свести уравнения к универсальным.

Эффективным методом упрощения уравнений является сравнительная оценка входящих в него членов. При этом:

- члены, имеющие в рабочем диапозоне второй порядок малости по сравнению с наибольшим, можно отбрасывать;

- члены, имеющие первый порядок малости, можно заменить константой.

Такой подход обычно называется переходом к автомодельной задачи. При упрощении модели рекомендуется заменять (аппроксимировать) сложные функции более простыми (интегрируемыми) вида , 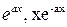и т.д. При этом важно, чтобы соблюдались граничные условия при х®0. Для нестационарных задач полезно осуществлять проверку решения в предельном случае .

Эффективно упрощение уравнений путем линеаризации отдельных его членов (т.е. их замены на линейные) вблизи предполагаемой точки экстремума (или в рабочем диапазоне протекания процесса).

Выбор метода решения математической модели является весьма специальным вопросом, ввиду их многообразия и

представляет собой специальную задачу, выходящую за рамку настоящего курса.

Процесс выбора модели заканчивается ее предварительным логическим, физическим и математическим контролем. При этом осуществляются следующие виды контроля: размерностей; порядков; характера зависимостей; экстремальных ситуаций; граничных условий; математической замкнутости, физического смысла; устойчивости модели.

Контроль размерностей сводится к проверке выполнения правила, согласно которому приравниваться и складываться могут только величины одинаковый размерности.

Контроль порядков слагаемых сводится к упрощению модели, о котором говорилось ранее.

Контроль характера зависимостей сводится к проверке направления и скорости изменения одних величин при изменении других. Они должны соответствовать физическому смыслу задачи.

Контроль экстремальных ситуаций сводится к проверке наглядного смысла решения при приближении параметров модели к нулю или бесконечности.

Контроль граничных условий состоит в том, что проверяется соответствие математической модели на границах области решения смыслу задачи.

Контроль математической замкнутости сводится к проверке того, что математическая модель дает единственное решение.

Контроль физического смысла связан контролем характера зависимостей и заключается в проверке непротиворечивости модели описываемому процессу или явлению.

Контроль устойчивости модели состоит в проверке того, что небольшое варьирование исходными данными не проводит к резким изменениям результатов решения.

Дата добавления: 2014-12-25