П.6. Похибка добутку

а = а₁ · а₂;

Перемножимо праві та ліві частини

, - відкидають.

Правила:

1. виділяють число з найменшою кількістю вірних значущих цифр.

2. заокруглюють решту множників до найменшої кількості цифр +1 запасну цифру

3. залишають в добутку стільки значущих цифр, скільки вірних значущих цифр має найменш точний множник.

Число вірних знаків добутку k співмножників (k ≤ 10) визначаються із 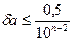. Отже, в добутку число вірних знаків на 1 або 2 одиниці менше n, якщо всі співмножники мають по n вірних значущих цифр. Якщо співмножники мають різну точність під (n) потрібно розуміти число вірних знаків найменш точного із співмножників.

При більшій ніж 10 кількості множників .

Приклад:

а = 84,76 · 8,436, всі цифри множників вірні, їх по 4; n = 4.

Тоді згідно яка випливає із ф-ли (3)

Тоді

Перевіримо А = а₁ · а₂ = 715,1

А = 715,1 ± 0,09, отже добуток має 3 вірні цифри.

0 ≤ - n + 1

п.7. Похибки частки та число вірних знаків частки.

Правила такі ж як і для добутку а = 5,735: 1,25 ≈ 4,66. Три значущих цифри, тому що найменш точне число (дільник) містить 3 вірні цифри.

А = 4,66 ± 0,02 – цифра сотих є сумнівною оскільки 0,02 > 0,05.

Число вірних знаків визначається із:

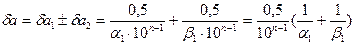
Якщо a₁ ≥ 2 і β₁ ≥2, то частка має n – 1 вірну значущу цифру. Якщо a₁ = β₁ = 1, то частка може мати n -2 вірні значущі цифри.

п.8. Похибки степеня та кореня.

dа = mδа₁, якщо а = а₁^m і .

п.9. Правила підрахунку кількості цифр в результаті.

Якщо не проводиться строгий розрахунок похибок, то рекомендується користуватися правилами підрахунку цифр:

1. При додаванні та відніманні наближених чисел в результаті потрібно зберегти стільки десяткових знаків, скільки їх є в наближеному числі з найменшою кількістю десяткових знаків.
2. При множенні та діленні в результаті слід зберегти стільки значущих цифр, скільки їх є в наближеному даному з найменшою кількістю вірних значущих цифр.
3. При піднесенні до 2 і 3 степеня – скільки значущих цифр є в основі степеня.
4. При добуванн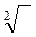і і – скільки значущих цифр є в підкореневому числі.
5. При обчисленні проміжних результатів варто зберігати на 1 цифру більше ніж рекомендують правила 1 ÷ 4. В кінцевому результаті ця запасна цифра відкидається.
6. Якщо деякі дані мають більше десяткових знаків (додавання чи віднімання) чи більше значущих цифр (інші дії) ніж інші, то їх попередньо треба заокруглити, зберігаючи лише 1 запасну цифру.
7. При обчисленні функцій потрібно підраховувати число значущих цифр в наближеному даному з найменшою кількістю значущих цифр в аргументі і скористатися таблицею функцій залишаючи стільки десяткових знаків, скільки їх є в аргументі +1 і в результаті останню цифру відкинути.
8. Якщо дані можна брати з довільною точністю, то для отримання результату з (m) вірними цифрами вхідні дані треба брати з такою кількістю цифр, які, згідно попередніх правил, забезпечують (m + 1) – цифру в результаті.

Ці правила даються в припущенні, що компоненти дій містять тільки вірні цифри і число дій невелике.

Наприклад: Розрахувати ,

де А = 7,45 ± 0,01

В = 50,46 ± 0,02

С = 15,4 ± 0,03. Визначити похибку результату.

а³ = 413,5; с² = 237,2

Залишені 3 значущі цифри, тому що в множниках найменша кількість значущих цифр – 3.

Підрахуємо похибки:

Отже

Наприклад: 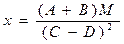, де

А = 2,754 ± 0,001

В = 11,7 ± 0,04

М = 0,56 ± 0,005

С = 10,536 ± 0,002

Д = 6,32 ± 0,008

Визначити похибки.

Знаходимо:

а + в = 2,75 + 11,7 = 14,45

c – d = 10,546 – 6,32 = 4,216

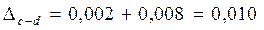
Тому

Отже

х = 0,46 ± 0,01;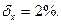

п.10. Розрахунок похибок функцій багатьох змінних.

Для оцінки операційних похибок можна ще робити так: Результат обчислень розглядають як функцію всіх операндів і результатів операцій і розкладають цю функцію в багатомірний ряд Тейлора. При малих похибках аргументу обмежуються лінійними членами ряду.

де

y · x	Ry = x; Rx = y
y / x	Ry = 1/x;
x^y	Ry = x^yln x; Rx = y · x^y^-1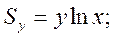
		1/2
e^x	e^x	x
10^x	10^xln 10	xln 10
lg x	1/x · ln 10	1/ln 10 lnx
ln x	1/x	1/ln x
sin x	cos x	x/tg x
cos x	-sin x	-x · tg x
tg x	1/cos^2 x	2x/sin 2x
arcsin x
arcos x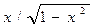
arctg x	1/(1 – x^2)	x/((1 - x^2) · arctg x)

Якщо функція f є функцією багатьох змінних, z = f(x₁, x₂, … x_n), то - абсолютна похибка

або обчислюється ще середньоквадратична похибка

Відносна похибка

або

По середньоквадратичній

Для перевірки точності слід використовувати по можливості більш прості методи.

1) Для обчислення спец. функцій – порівняння з відомими точними значеннями.

2) Точність коренів нелінійних рівнянь f(x) = 0 і систем рівнянь оцінюють по нав’язках рівнянь. (значення лівої частини рівняння при підстановці обчислених значень коренів)

При використанні прямих (точних) методів обчислень, коли точно відомо число операцій, похибки можна оцінити наперед. При використанні непрямих методів (числове інтегрування, сумування ∞ рядів, розв’язок рівнянь методом послідовних наближень) точне значення результату може бути отримане тільки після ∞ числа операцій. Практично ж виконується тільки скінчене число операцій, то виникає методична (залишкова похибка). Тому при використанні непрямих методів алгоритм обчислень потрібно вибирати так, щоб мінімізувати суму операційної та методичної похибки.

п.11. Визначення допустимої похибки аргументів за

допустимою похибкою функції.

Це є оберенена задача до попередніх.

Ця задача має однозначний розв’язок лише для функцій одної змінної y=f(x); якщо ця функція диференційовна і f¢(x) 0, то

(1)

Для функції декількох змінних задача розв’язується лише при введенні яких-небудь додаткових обмежень. Наприклад, якщо значення одного з аргументів на багато важче виміряти чи обчислити з більшою точністю ніж значення інших аргументів, то похибку саме цього аргументу треба узгодити з потрібною похибкою функції.

Якщо значення всіх аргументів можна однаково легко обчислити з будь-якою точністю, то зазвичай застосовують принцип рівних впливів, вважаючи, що у формулі

(2)

всі доданки рівні між собою; це дає формулу

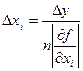(i=1,2,…,n) (3)

На практиці часто зустрічаються задачі проміжного типу між вказаними крайніми випадками. Ми розглянемо відповідні приклади.

Приклад 1. З якою точністю потрібно виміряти кут у першій чверті, щоб отримати значення sinx з п’ятьма вірними знаками.

Розв’язання. Якщо відомо, що кут х>6°, так що sinx>0.1, то потрібно визначити так, щоб виконувалась нерівність .У відповідності з формулою (2) . Достатньо взяти , тобто виміряти кут з точністю до 1”. Якщо, більше того відомо, що кут х>60° і, значить, cosx<0.5, то потрібно скористатися формулою (1).

Приклад 2. Знайти допустиму абсолютну похибку наближених величин х=15.2, у=57 , для яких можливо знайти значення функції

з точністю до двох десятих знаків (після коми)

РОЗВ’ЯЗАННЯ: Знаходимо

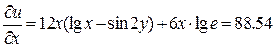
За умовою u=0,005. Тоді згідно принципу рівних впливів за формулою (2) знаходимо

,

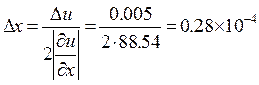Якщо функція залежить тільки від одного аргумента (n=1), то маємо не рівність С1 і для досяжності потрібної точності достатньо взяти

У випадку n>1 іноді рекомендують відвести похибці кожного аргумента

рівну долю, вибрати з умови ,

В іншому випадку пропонують взяти усі похибки рівними, максимально можливими, т.с. покласти

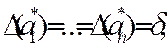де .

п.12. Точність представлення чисел в комп'ютері

Машинне представлення чисел відрізняється від точного представлення чисел. Представлення деякого числа а в розрядній сітці машини - це сукупність 0 і 1. Точно переводяться в двійкову систему числення цілі числа. При переведенні дробової частини в двійкову систему числення в багатьох випадках отримується нескінчений періодичний або неперіодичний дріб. Крім цього в машинному представленні можуть бути точно зображені числа кратні 2. Отже, деяке число х в двійковій системі числення запишеться так:

Коефіцієнт це 0 або 1. Т. ч. через обмеженість розрядної сітки та приведені вище причини числа представляються в розрядній сітці комп’ютера наближено. Для характеристики точності представлення чисел використовують абсолютну та відносну похибки. Нехай точне значення деякого числа = а, а його машинне представлення [а], тоді абсолютна похибка

Розглянемо форму представлення чисел з фіксованою крапкою. Нехай крапка фіксується перед старшим розрядом._ _ _ _ _ За означенням, абсолютна похибка представлення чисел у цьому випадку = половині молодшого розряду ® – значення молодшого розряду, а похибка

– вона є постійною.

Відносна похибка буде залежати від величини числа а в комп’ютері, бо воно може приймати max і min значення

а_max:

а_min:

Тоді відносна похибка повинна змінюватись в межах

,

(1)

(2)

Отже, відносна похибка залежить від величини числа і коливається від значення (1) для великих чисел до значення (2) для малих чисел і може ® 100%

Розглянемо представлення у формі з плаваючою крапкою (А-мантиса). Абсолютна похибка 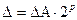(DА-абсолютна похибка мантиси). Оскільки мантиса має вигляд 0. _ _ _ …, то 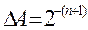. Отже, абсолютна похибка буде залежати від порядку!!! Оскільки порядок це ціле число, то його

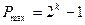, а

Видно, що min значення абсолютної похибки буде при найбільшому від’ємному значенні порядку, тобто

Відносна похибка 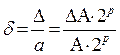буде залежати від величини мантиси. Мантиса в нормалізованому вигляді приймає і (0.11111…...). Тоді ; ; Отже визначається кількістю розрядів мантиси і не залежить від порядку числа.

Є дві форми представлення 2-их чисел в електронних обчислювальних пристроях:

з фіксованою крапкою та з "плаваючою" крапкою.

Нехай в розрядній сітці необхідно розмістити 2-е число, що містить цілу та дробову частину. Якщо для розміщення цілої частини числа відводиться k- комірок n- розрядної сітки то, без врахування знаку, для розміщення дробової частини залишиться (n-k) вільних комірок. Така форма представлення двійкових чисел називається формою з фіксованою крапкою.

Якщо кількість розрядів в дробовій частині числа, що розміщується > за (n-k), то деякі молодші розряди будуть за межами розрядної сітки і обчислювальним пристроєм не сприймуться. Отже, будь-яке 2-ове число менше за 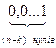сприймається за нульове і називається "машинним" нулем. В результаті відкидання молодших розрядів дробової частини числа, розташованих за межами розрядної сітки, виникає похибка представлення 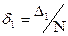(яка може наближатися до 100%!).

Показникова форма чи форма з "плаваючою" крапкою застосовується для розширення діапазону та зменшення відносної похибки представлення чисел в обчислювальних пристроях.

,

де р – порядок, q –10 або 2, а– дріб <1, тобто мантиса в нормалізованому вигляді

(в старшому розряді мантиси немає нуля).

Якщо після виконання арифметичних операцій результат виявляється не нормалізованим, то перед занесенням числа в пам'ять відбувається його нормалізація, тобто зсув мантиси наліво на відповідну кількість розрядів та зменшення порядку числа на відповідне число одиниць.

Наприклад, нормалізований вигляд числа 1110110,011₍₂₎ є 0,1110110011·10¹¹¹⁽⁷⁾

Знак порядку

Знак мантиси К- мантиса (n-k)- код порядку

Наприклад, якщо довжина розрядної сітки n=16, а число розрядів, що відводиться під мантису k=10.

Форма представлення	крапка
фіксована	“плаваюча”
Границя	нижня	верхня	нижня	верхня
Діапазон Чисел
Діапазон зміни відносних похибок

Отже, діапазон представлення чисел з фіксованою крапкою складає 16 двійкових розрядів, а в формі з "плаваючою" крапкою - 127 розрядів.

Макс. відносна похибка 100% для чисел з фіксованою крапкою і 0.1% для чисел з "плаваючою" крапкою.

Використовують вбудовані математичні співпроцесори, що працюють з числами у формі "плаваючої" крапки.

Множина дійсних чисел, що використовуються є безмежною. При розрахунку на комп’ютері множина цілих та дійсних чисел є обмеженою. Це зв’язано з обмеженістю розрядної сітки комп’ютера. Наприклад, якщо для представлення цілого числа відводиться 16 розрядів, то максимальне додатне число N=2¹⁶-1. Аналогічно обмежується мінімальне число. Для дійсних чисел N=0.a₁a₂a₃En порядок n задає обмеження по величині, а кількість цифр у мантисі задає дискретність розподілу цифр на числовій осі. Наприклад, в 10-вій системі числення нехай для представлення мантиси відводиться 4 розряди, то всі числа, які лежать між 0.3552 і 0.3551 в машині будуть представлені машинним нулем. Внаслідок цього числа будуть представлені наближено N=0.a₁a₂a_{3 ?}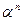

Макс.відносна похибка, яка виникає при заокругленні чисел за означенням дорівнює

, де a -основа системи числення, k-кількість розрядів мантиси.

Наприклад, якщо використовується 16-система числення і для мантиси використовується 6 розрядів, то похибка

Якщо не виконувати заокруглення, а просто відкидати лишні розряди, то максимальна відносна похибка зросте в 2 рази.

п.13. Стійкість, коректність та збіжність.

Нехай величина х-це початкове вхідне значення; y-шукана величина або розв’язок. Якщо малим змінам вхідної то говорять, що задача є стійкою по вхідних параметрах. Це означає, що розв’язок неперервно залежить від початкових значень, тобто малі похибки вхідних даних приводять до малих похибок результату.

Задача називається поставленою коректно, якщо для деякого класу вхідних даних її розв’язок існує, єдиний і стійкий у вхідних даних. Якщо розв’язок задачі не стійкий (малі похибки вхідних даних сильно впливають на результат або дають зовсім неправильний результат) то вона є не коректно поставленою. Існують методи розв’язку некоректних математичних задач, при цьому використовують методи регуляризації. Вводячи параметр регуляризації, задача стає коректно поставленою, а її розв’язок при прямуванні параметра регуляризації до нуля переходить у розв’язок некоректно поставленої задачі.

Під збіжністю числового методу розуміють, що розв’язок ® істинного. При цьому будується деякий ітераційний процес. Він представляє деяку послідовність дій, які періодично повторюються. Кожне із таких повторень називається ітерацією. В результаті ітерацій отримуємо послідовність розв’язків: x₁,x₂,x₃,…,x_n. Числовий метод називається збіжним, якщо 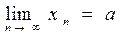(a- точний розв’язок)

Числове інтегрування

Обчислення скалярних адитивних величин зводиться до сумування нескінченного великого числа нескінченно малих складових такого вигляду

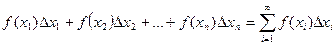
- наближене,

- точне.

Нехай на скінченому відрізку [а,b] задана неперервна функція f(x). Нехай

1. Розіб'єм відрізок [а, b] довільним числом на n частинних відрізків точками . Позначимо довжину кожного частинного відрізка через (i=0,1,2,,,n-1)

3. Виберемо довільно в кожному частинному відрізку точку (i=0,1,2,,,,n-1)

4. Складемо добуток значення функції f в точці і на довжину і-го відрізку

5. Цей добуток дає площу елементарного і-го прямокутника

6. Просумуємо отримані добутки - називається інтегральною сумою.

Ну а інтеграл ,якщо існує скінчена границя.

Для наближеного інтегрування функції розроблено багато числових методів. Суть всіх методів зводиться до того, що значення інтеграла обчилюється наближено за формулами: - квадратурна! (1)

Дійсні числа називаються коефіцієнтами та вузлами квадратурної формули. Величина називається залишковим членом або похибкою квадратурної формули.

Замінюючи інтеграл квадратурною сумою ми нехтуємо залишковим членом R(f).

Виконуючи обчислення за формулою (1) завжди оперують не з точними, а з наближеними значеннями підінтегральної функції f(x ) і коефіцієнтів A . Похибка, з якою задані значення f(x ) та A , переноситься і на квадратурну суму-це так звана неусунена похибка R формули (1). Якщо A - точні числа, а значення f(x ) обчислені з похибкою 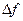то значення квадратурної суми буде обчислена з неусуненою похибкою

При знаходженні квадратурної суми всі проміжні обчислення рекомендується проводити з 1-2 запасними цифрами. Це дає можливість знехтувати похибками заокруглень в проміжних обчисленнях. Але при відкиданні запасних цифр в кінцевому результаті необхідно враховувати заключну похибку заокруглення Отже - сумарна похибка числового інтегрування.

Геометрично загальний підхід до рішення задачі наближеного інтегрування функцій полягає в тому, що в криволінійну трапецію, площа якої дорівнює шуканому інтегралу, вписують або описують частинні прямокутники,трапеції або параболи, знаходять їх площі, а потім сумують. В результаті отримують наближене значення шуканого інтегралу, тому що при цьому графік функції f замінюється на деяку ламану лінію. У відповідності до вибору геометричної фігури для обчислення інтегралу розрізняють формули:

прямокутників

трапеції

парабол (Сімпсона)

Для отримання цих формул відрізок інтегрування ділять на частинні відрізки однакової довжини.

Формула прямокутників

[а,b] ділять на n рівних частин точками так, що Точки розбиття утворюють арифметичну прогресію з різницею h. Ці точки називаються вузлами. Потім у вузлах обчислюють ординати для 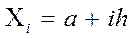(i=0,…n)

На частинних відрізках будуть прямокутники, висота яких дорівнює значенню в якійсь точці кожного частинного відрізку.

Тоді добуток -дасть площу частинного прямокутника, а сума таких добутків дасть площу фігури сходинки, що представляє наближене значення інтегралу.

Якщо обчислюють в лівих кінцях відрізків, то отримують формулу лівих прямокутників

Правих

Середніх

I=

Формула трапеції

На кожному частинному відрізку будується трапеція.

Площі частинних трапецій дорівнюють:

y

x

+ .

ФОРМУЛА СІМПСОНА

- рівняння параболи

виразимо А і С через

Тоді площа під параболою

Тепер обчислимо інтеграл. Для цього відрізок 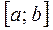розіб’ємо на 2n рівних частин довжиною

або

, де

Похибки

Сер. Прям.

Трапецій

Сімпсона

Але для оцінки похибки інтегрування використовують метод автоматичного вибору кроку інтегрування для досягнення заданої точності.

Алгоритм

1. при початковому n візьмемо крок

2. обчислюємо

3. зменшуємо h в два рази і для нього обчислюємо

4. порівнюємо два значення

5. отримане значення R порівнюємо з попередньо заданою точністю E.

Якщо , то І повторюється 3,4 і 5 пункт до тих пір поки .

6. Якщо , то - значення інтегралу з заданою точністю Е.

Універсальні алгоритми обчислення коренів

нелінійних та трансцендентних рівнянь

Універсальні алгоритми обчислення коренів рівнянь засновані на тому, що виходять з якого-небудь уже відомого наближеного значення х₀ одного з коренів, яке потім покращують до заданої степені точності. При цьому немає суттєвого значення як знайдено це перше наближення шуканого кореня. Часто перше наближення отримують за допомогою грубого попереднього підрахунку або графічно. (Точки перетину графіка функції F(x) з віссю абсцис дають наближене значення шуканих коренів з похибкою, яка залежить від масштабу та точності графіків).

Алгоритми наближеного знаходження коренів нелінійних рівнянь складаються із 2 етапів:

1. Відшукання достатньо малих відрізків, що належать області визначення рівняння, в кожному із яких знаходиться один і тільки один корінь рівняння. Це етап відділення коренів рівняння або визначення відрізка ізоляції коренів.

2. Обчислення коренів з наперед заданою точністю, якщо відоме деяке початкове наближення кореня у відрізку ізоляції. Це етап уточнення наближених коренів.

F(x) = P_n(x) = a_nxⁿ + a_n-1x^n-1 +…+a₀

n = 1 – лінійне

n ≥ 2 – нелінійне

f(x) = φ(x) (1)

f(x) - φ(x) = 0

F(x) = 0 (2)

Трансцендентні, якщо F(x) містить тригонометричну, показникову або логарифмічну функцію.

Дата добавления: 2015-05-23