СМО типа M/G/m/. Формулы Хинчина-Поллачека

Рассмотрим одноканальную СМО с неограниченной очередью, простейшим потоком заявок и произвольным распределением времени обслуживания(M/G/1/). Предполагается простейший поток заявок интенсивностью 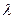, время обслуживания – произвольное распределение с математическим ожиданием и коэффициентом вариации времени обслуживания , то среднее число заявок в очереди 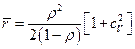, среднее число заявок в системе обслуживания , , 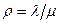среднее число заявок, находящихся на обслуживании равно 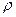. (Ранее для одноканальной СМО получено: 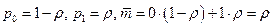) см Таблицу).

По формулам Литтла: среднее время пребывания заявки в очереди (в ожидании начала обслуживания) , а в системе обслуживания - .

Отметим, что если время обслуживания распределено по экспоненциальному закону, то и получаются формулы для простейшей одноканальной СМО.

Если 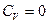, т.е. рассматривается «регулярное» обслуживание, то уменьшаются.

Севастьяновым Б.А. (1959г.) доказано, что формулы Эрланга для финальных вероятностей m-канальной СМО с отказами справедливы не только при показательном, но и при произвольном распределении времени обслуживания (M/G/m/0) (Севастьянов Б.А. Формулы Эрланга в телефонии. //Труды III Математического съезда, том IV. – М.: Издательство АН СССР, 1959 – с.)

УПОРЯДОЧЕННЫЕ СИСТЕМЫ ОБСЛУЖИВАНИЯ. ЗАДАЧА ПАЛЬМА.

Ранее рассматривались ситуации, когда все каналы равноправны, любое требование могло попасть на обслуживание в любой канал, что не во всех СМО имеет место.

Рассматривается случай, когда каналы обслуживания неравноправны с точки зрения поступления требований на них. Наиболее простая организация этого типа является такая, когда все каналы обслуживания пронумерованы. Такая система называется упорядоченной. Поступающие требования распределяются между каналами согласно их номерам – первым загружается канал с номером один; если он занят в момент поступления заявки (требования), то к обслуживанию её принимает канал под номером два и т.д. Таким образом, требование поступает на обслуживание в свободный канал с наименьшим порядковым номером (Хинчин А.Я. Математические методы ТМО. – М.: Издательство АН СССР, 1955). Возникает вопрос о загруженности каналов обслуживания при стационарном режиме функционирования упорядоченной системы.

Рассматривается упорядоченная система каналов обслуживания  их конечное или бесконечное число. На входе в систему и канал простейший поток с интенсивностью .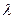

ТЕОРЕМА. Если на канал 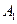поступает простейший поток требований, то на поступает стационарный, ординарный поток с ограниченным последействием.

Закон распределения времени обслуживания – любой, а через 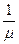обозначим среднее время обслуживания одного требования одним каналом.

Требуется охарактеризовать степень загрузки СМО, в частности, найти вероятность того, что одновременно заняты каналов.

◄ Пусть 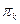- вероятность того, что первые 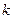каналов заняты.

Для 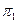: СМО с одним каналом - доля времени, в течение которого каналы заняты. Получено из более общей формулы

Для : (вероятность того, что заняты каналы 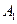и 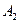) – СМО с двумя каналами обслуживания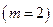 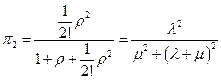, - вероятность того, что заявка поступит на 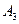и т.д.

Общий случай: и легко убедиться, что убывает с ростом , независимо от значения .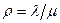

Уточним, что означает вероятность потери требования первыми каналами в силу их занятости, но эта характеристика не даёт полной информации о занятости конкретного канала, например . Например, может оказаться, что канал занят, а в это время один из каналов 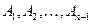уже освободился. Обозначим 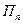вероятность того, что канал занят. Если заняты каналы , то это означает, что:

1. заняты каналы .
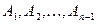2. занят канал .

Вероятность первого события 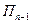, а второго - 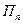. По теореме умножения вероятносте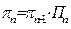й или .

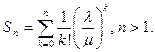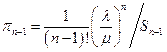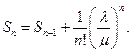Обозначим Тогда , или С учётом этого

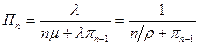, Уточним, что для

Таким образом, зная 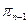(т.е. вероятность того, что первые 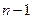каналов заняты), можно найти вероятность того, занят канал ►

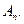ЗАДАЧА 13. Упаковочные автоматы установлены последовательно и пронумерованы в том порядке, в каком установлены. Первым загружается автомат под номером один. Если он занят, то к обслуживанию приступает второй автомат и т.д. Среднее время упаковки одного изделия 3.24 секунды, т.е. 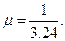Поток готовых изделий (из разных цехов) простейший с интенсивностью

◄ Используя приведённые выше формулы легко получить при :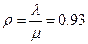

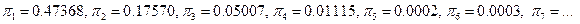
Эти результаты позволяют прогнозировать степень загрузки автоматов, сроки их выхода из строя и т.д. ►

Можно рассмотреть обобщение предыдущей задачи: Равноправные каналы объединены в пронумерованные группы. Сначала требование поступает в первую группу и т.д. Пусть в 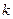-ой группе объединены каналов. Обозначим через 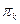- вероятность того, что заняты все каналы всех групп до 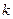- ой включительно:

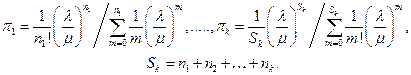
При вычислении исходим из рассмотрения 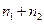каналов с отказами.

ЗАДАЧА 14. Система противоракетной обороны (ПРО) государства Эффения имеет 3 зоны и каждая из зон состоит из 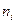противоракетных установок (ПРУ), 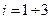. Все ПРУ одинаковы и каждая может обстреливать одну цель (ракету). Время обстрела не зависит от числа летящих ракет. Поток ракет интенсивности 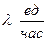, среднее время обслуживания (обстрела) - 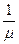. Обстрел ракеты обозначает её поражение. Те ракеты, что не были обстреляны в первой зоне, попадают во вторую зону и т.д. Какова вероятность прорыва ракетой каждой зоны?

◄ . Вероятность прорыва ракетой первой зоны

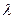Можно также определить сколько потребуется ПРУ для того, чтобы вероятность прорыва была меньше заданной величины . При известных и 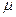количество требуемых ПРУ находим как решение неравенства .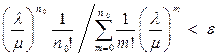

Свойства инвариантности для пуассоновских потоков.

Инвариантность пуассоновского потока (ПП) относительно операции суммирования. При суммировании конечного числа независимых ПП с интенсивностями суммарный поток также будет пуассоновским с интенсивностью 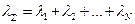. Независимость потоков означает, что числа событий, поступивших в двух произвольных интервалах разных потоков, статистически независимы.

Инвариантность ПП относительно операции случайного просеивания (случайного “разрежения”). Если к каждому событию ПП, который имеет интенсивность 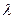, применяется операция просеивания (“разрежения”), заключающаяся в выбрасывании с вероятностью p события из потока, то оставшийся поток событий будет пуассоновским с интенсивностью 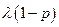, а поток выброшенных событий также будет с простейшим с интенсивностью .

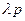Для доказательства необходимо проверить три характеристических свойства ПП: стационарность, ординарность и отсутствие последействия. Поскольку операция разрежения проводится одинаково при любом значении 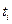, это даёт стационарный результирующий поток. Ординарность сохраняется очевидным образом, так как количество точек может только уменьшаться. Наконец отсутствие последействия сохраняется в связи с тем, что исключение точек происходит каждый раз независимо от предыдущих результатов.

Пуассоновский поток интенсивности 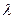при обслуживании в СМО (одно- и многоканальной) с неограниченным числом мест для ожидания и показательно распределённым временем обслуживания остаётся пуассоновским той же интенсивности.

Предположим, что на вход одноканальной СМО в моменты времени 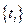поступают требования. Моменты 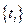образуют пуассоновский поток с интенсивностью 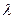. Длительности обслуживания предполагаются взаимно независимыми случайными величинами с функцией распределения . Требования, заставшие систему занятой, становятся в очередь и обслуживаются в порядке поступления (то есть рассматривается СМО M/M/1).

ТЕОРЕМА. Случайная последовательность моментов времени , в которые требования после обслуживания поступают в систему M/M/1, соответствует в установившемся режиме работы пуассоновскому потоку с интенсивностью .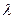

◄ Покажем, что число требований 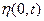, которые были обслужены в интервале (0, t), является пуассоновской случайной величиной, причем .

Пусть 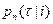- условная вероятность того, что в промежуток времени 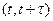произошло обслуживаний при условии, что за это же время в системе находилось заявок. Поскольку рассматривается установившиеся состояние СМО, то вероятность нахождения заявок в одноканальной СМО с бесконечной очередью .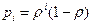

Рассмотрим малый промежуток 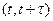. Появление события в этом промежутке определяется величиной вероятности .

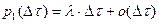При этом возможны три случая:

1) если за время 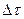приходит новая заявка с вероятность 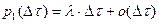, то число заявок возрастает на единицу, а число обслуженных заявок не изменится, чему будет соответствовать условная вероятность ;

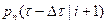2) если за время 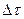с вероятностью 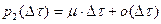заканчивается обслуживание одной заявки, то в промежутке число окончаний обслуживания будет равным 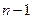, при этом обслуженная заявка покинет систему и число заявок в системе будет ровно 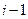, соответственно условная вероятность будет равна ;

3) если за время 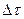не поступит ни одной заявки и не закончится ни одно обслуживание с вероятностью 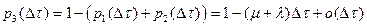, то этому состоянию по определению будет соответствовать условная вероятность .

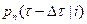Тогда условные вероятности, связаны соотношением

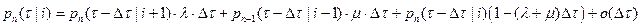Переходя к пределу при получаем ОДУ:

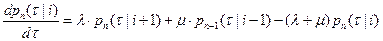(20)

Положим 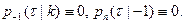Используя формулу полной вероятности

(21)

где - вероятность того, что за время 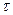в системе произойдет окончаний обслуживаний, переходим от условных вероятностей к безусловным. Очевидно, что из (21) следует:

(22)

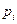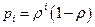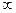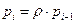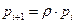Умножим обе части (20) на , определяемые из и произведём суммирование обеих частей (20) по от 0 до . При этом или . С учётом этого обстоятельства и соотношение (22), для 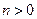справедливо:

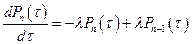(23)

Очевидно, что

(24)

Проинтегрируем (23) и (24) с начальными условиями 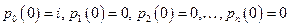, которые отражают тот факт, что за нулевой отрезок времени не происходит ни одного события.

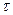Система уравнений (23), (24) с указанными начальными условиями полностью совпадает с системой ОДУ, которая определяет вероятности попаданий событий на интервал пуассоновского потока. Отсюда следует, что выходной поток – пуассоновский.

Подробный вывод уравнения (23). Умножаем обе части (20) на 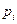и суммируем от 0 до 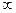; учитывая, что :

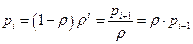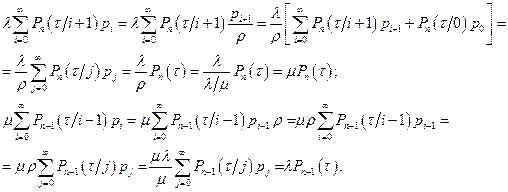
В последнем случае учтено, что Аналогично В итоге для :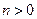

Поскольку положено, что 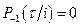, то с помощью таких же выкладок получим :

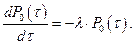
В связи с этим различные подсистемы в многофазной системе СМО можно рассматривать независимо друг от друга как системы, находящиеся под воздействием одного и того же потока заявок интенсивности 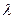и потоки обслуживания в общем случае с различными интенсивностями

СЛЕДСТВИЕ. Состояние СМО характеризуется вероятностью некоторого распределения заявок по каждой из систем

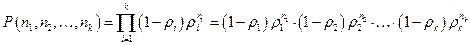(25)

с условием нормировки

(26)

Поскольку для среднего числа заявок в отдельной подсистеме , то для среднего числа заявок в многофазной СМО:

(27)

Для многоканальной СМО:

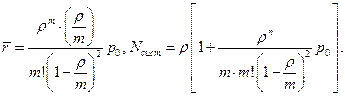
Используя эти формулы, можно получить выражения, аналогичные (25), (26) и (27) для случая применения таких СМО в качестве подсистем многофазных СМО.

Дата добавления: 2015-06-25