Пример контрольной работы и образец ее выполнения

Парабола

Гипербола

Эллипс

Кривые второго порядка

Условие параллельности прямой и плоскости

Условие параллельности прямой и плоскости эквивалентно условию перпендикулярности векторов 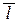(m;n;p) и (A;B;C), и выражается равенством нулю скалярного произведения этих векторов:

Am+Bn+Cp=0.

3.11.3. Условие перпендикулярности прямой и плоскости эквивалентно условию параллельности векторов 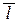(m;n;p) и (A;B;C), и выражается пропорциональностью координат этих векторов:

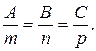
Эллипс – множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости F₁ и F₂, называемых фокусами, есть величина постоянная, равная 2а.

При этом не исключается совпадение фокусов эллипса, в этом случае получаем окружность.

Пусть точка М (х,у) – некоторая точка плоскости. Обозначим через r₁ и r₂ расстояния от точки М до точек F₁ и F₂ соответственно. Согласно определению эллипса равенство:

r₁+r₂=2a

является необходимым и достаточным условием расположения точки М (х,у) на данном эллипсе.

- каноническое уравнение эллипса.

Свойства эллипса.

1) Эллипс симметричен относительно осей Ох и Оу и точки О (0;0) – центра эллипса.

Точки пересечения эллипса с осями координат А₁ (а; 0) и А₂ (-а; 0), В₁ (0 ;b) и B₂ (0 ;-b) называются вершинами эллипса.

Отрезки А₁А₂=2а и В₁B₂=2b называются соответственно большой и малой осями эллипса.

2) Эллипс содержится внутри прямоугольника |x|£a, | y|£b. В самом деле, из канонического уравнения вытекает, что . Эти неравенства эквивалентны неравенствам |x|£a, | y|£b.

Отношение расстояния между фокусами к длине большой оси эллипса называется эксцентриситетом эллипса:

е=с/а.

Учитывая, что b²=a²-c², получим:

.

Из этой формулы видно, что эксцентриситет эллипса меньше единицы.

Чем больше эксцентриситет эллипса, тем меньше отношение малой полуоси эллипса b к его большой полуоси а, и значит, тем более сплющенным будет эллипс.

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек плоскости F₁ и F₂, называемых фокусами, есть величина постоянная, равная 2а.

Точки F₁ и F₂ имеют координаты F₁ (c, 0) и F₂(-c, 0).

Пусть точка М (х,у) – некоторая точка плоскости. Обозначим через r₁ и r₂ расстояния от точки М до точек F₁ и F₂ соответственно. Согласно определению гиперболы равенство:

|r₁-r₂|=2a

является необходимым и достаточным условием расположения точки М (х,у) на данной гиперболе.

Уравнение гиперболы в данной системе координат примет вид:

- каноническое уравнение гиперболы,

где b²=c²-a².

Если а=b, то гипербола называется равносторонней.

Свойства гиперболы.

1) Гипербола симметрична относительно осей Ох и Оу и точки О (0;0) – центра гиперболы.

2) Гипербола состоит из двух частей, называемых ветвями гиперболы.

Точки пересечения гиперболы с осью Ох А₁ (а; 0) и А₂ (- а; 0) называются вершинами гиперболы.

Отрезок А₁А₂=2а называется действительной осью гиперболы.

3) Прямые и называются асимптотами гиперболы ( ветви гиперболы неограниченно приближаются к этим прямым).

Отношение расстояния между фокусами к длине действительной оси эллипса называется эксцентриситетом гиперболы:

е=с/а.

Учитывая, что b²=с²-а², получим:

.

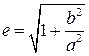Из этой формулы видно, что эксцентриситет гиперболы больше единицы.

Эксцентриситет гиперболы можно рассматривать как числовую характеристику величины угла между ее асимптотами, т.к. отношение есть тангенс половины угла между асимптотами гиперболы.

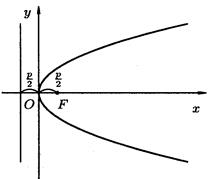
Параболой называется множество точек плоскости, каждая из которых одинаково удалена от данной точки F, называемой фокусом, и данной прямой l, называемой директрисой.

Расстояние от фокуса F до директрисы l называется параметром параболы и обозначается через р.

Пусть ось Ох проходит через фокус F перпендикулярно директрисе, а начало координат расположено посередине между фокусом и директрисой. Тогда F (p/2; 0), а уравнение директрисы х=-р\2.

у²=2рх

– каноническое уравнение параболы.

Свойства параболы.

1) Парабола симметрична относительно оси Ох (Ох - ось симметрии параболы), т.к. в каноническом уравнении параболы величина у фигурирует в четной степени.

Парабола проходит через начало координат, точка О (0;0) – вершина параболы.

Отметим, что кривая у²=2рх при р<0 также является параболой, которая располагается в левой полуплоскости.

Вариант №0

1. Вычислить произведение матриц

.

Дата добавления: 2017-01-13