Вычислить определитель 1 страница

Вычислить определитель

.

3. Найти обратную матрицу

.

4. Решить системы линейных уравнений.

а) Методом обратной матрицы.

б) Методом Крамера.

в) Методом Гаусса.

а) б) в)

5. Написать разложение вектора по базису :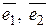

.

6. Установить, являются ли векторы линейно-зависимыми:

.

7. Найти площадь параллелограмма, построенного на векторах и :

.

8. Составить уравнение прямой, проходящей через две точки М₁(1, 5), М₂(3, 3) и найти расстояние от точки Р(1,-2) до полученной прямой.

9. Найти угол между прямыми:

.

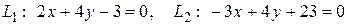10. От общего уравнения прямой

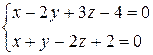
перейти к каноническому уравнению.

11. Написать уравнение плоскости, проходящей через три заданные точки

.

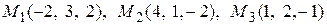12. Найти расстояние от точки М до плоскости p:

.

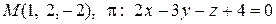13. Найти проекцию точки М на плоскость p:

.

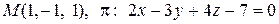14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически

.

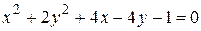Решение варианта №0

1. Вычислить произведение матриц

.

Решение:

Умножение матриц можно произвести только в том случае, если число столбцов первой матрицы равно числу строк второй матрицы. В данном случае это условие выполняется, поэтому произведение матриц можно вычислить. По правилу умножения матриц «строка на столбец» находим

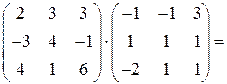
Ответ: .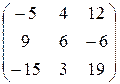

.

Решение:

Используя свойства определителей, обратим в нуль все, кроме одного, элементы его первого столбца. Для этого произведем следующие действия: 1) к элементам 2-ой строки прибавим элементы 1-ой строки, 2) к элементам 3-ей строки прибавим элементы 1-ой строки, умноженные на 2, 3) к элементам 4-ой строки прибавим элементы 1-ой строки, умноженные на -2.

Полученный определитель разложим по элементам 1-го столбца:

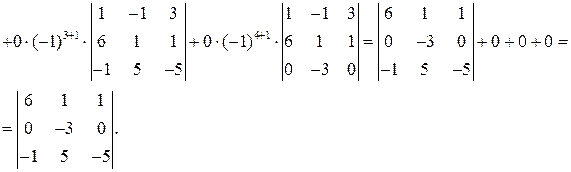
Теперь полученный определитель можно разложить по 2-ой строке (т.к. она содержит два нуля):

Ответ: 87.

3. Найти обратную матрицу

.

Решение:

Обратная матрица вычисляется по формуле:

,

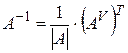где | А | - определитель исходной матрицы А, | А| ¹0.

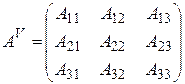- матрица алгебраических дополнений для исходной матрицы А.

Вычислим определитель исходной матрицы по правилу «треугольников», он не должен быть равен 0.

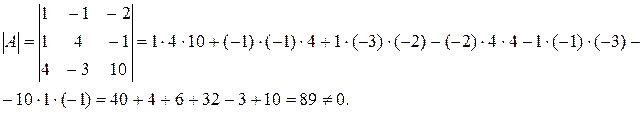
Вычислим алгебраические дополнения элементов исходной матрицы:

,

,

,

,

,

,

,

,

.

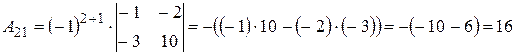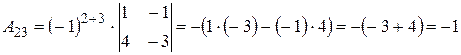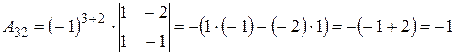Составляем матрицу из алгебраических дополнений и транспонируем ее:

, .

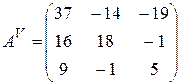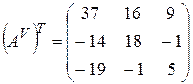Подставляем полученные выражения в формулу:

.

Ответ:

4. Решить системы линейных уравнений.

а) Методом обратной матрицы.

б) Методом Крамера.

в) Методом Гаусса.

а) б) в)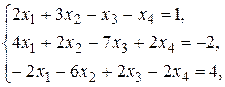

Решение:

а) Метод обратной матрицы.

Решение ищется по формуле:

,

где - матрица коэффициентов системы,

- столбец свободных членов.

Найдем обратную матрицу для матрицы А:

,

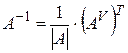где | А | - определитель исходной матрицы А, | А| ¹0.

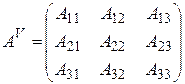- матрица алгебраических дополнений для исходной матрицы А.

Вычислим определитель исходной матрицы по правилу «треугольников», он не должен быть равен 0.

Вычислим алгебраические дополнения элементов исходной матрицы:

,

,

,

,

,

,

,

,

.

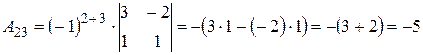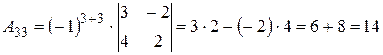Составляем матрицу из алгебраических дополнений и транспонируем ее:

, .

Затем подставляем полученные выражения в формулу:

.

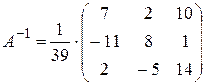Теперь найдем X, вычислив произведение А ^-1× В:

Таким образом, получим решение .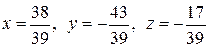

Ответ: .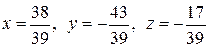

б) Метод Крамера.

Если определитель системы D¹0, то решение системы можно найти по формулам Крамера:

,

где D₁, D₂, D₃ – определители, полученные путем замены соответствующего столбца на столбец свободных членов.

Вычислим определители по правилу «треугольников»:

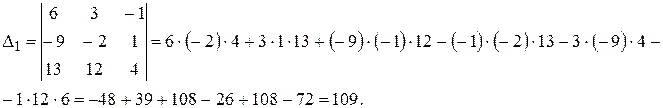
Подставляем полученные значения в формулы Крамера, и находим решения системы:

.

Ответ: .

в) Метод Гаусса.

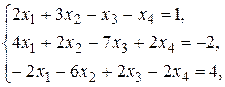
Составим расширенную матрицу коэффициентов системы:

.

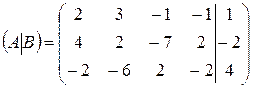Приведем её путем элементарных преобразований к трапециевидному виду: 1) к элементам 2-ой строки прибавим элементы 1-ой строки, умноженные на -2, 2) к элементам 3-ей строки прибавим элементы 1-ой строки, 3) умножим элементы 3-ей строки на -4, 4) к элементам 3-ей строки прибавим элементы 2-ой строки, умноженные на 3.

Ранг матрицы коэффициентов равен рангу расширенной матрицы, значит, система совместна. При этом ранг матрицы коэффициентов меньше числа неизвестных, поэтому система имеет множество решений.

Три неизвестных примем за базисные (т.к. ранг матрицы коэффициентов равен 3), одна неизвестная будет свободной.

Выделим минор третьего порядка, не равный нулю:

Тогда 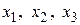будут базисными переменными, - свободной переменной.

Составим систему уравнений, соответствующую полученной матрице:

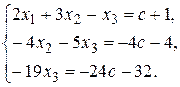
Теперь вычислим значения неизвестных.

Из третьего уравнения получаем х ₃:

,

Из второго уравнения находим х ₂:

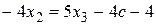, Из первого уравнения находим х ₁:

,

Ответ: , , , .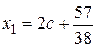

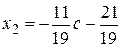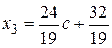5. Написать разложение вектора по базису :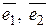

.

Решение:

Разложение вектора по базису 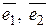имеет вид:

,

где a и b - координаты вектора в данном базисе.

Подставим координаты векторов в указанное равенство:

.

Получим систему уравнений для определения координат вектора :

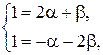
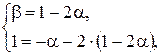
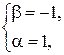
Получаем следующее разложение по базису для вектора :

.

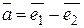Ответ: .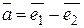

6. Установить, являются ли векторы линейно-зависимыми:

.

Решение:

Векторы являются линейно зависимыми, если их смешанное произведение равно нулю, и являются линейно независимыми, если их смешанное произведение не равно нулю.

Вычислим смешанное произведение данных векторов в координатной форме:

Таким образом, векторы линейно независимы.

Ответ: векторы линейно независимы.

7. Найти площадь параллелограмма, построенного на векторах

и : .

Решение:

Площадь параллелограмма, построенного на векторах 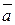и 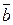, численно равна модулю векторного произведения данных векторов, и вычисляется по формуле:

.

Найдем векторное произведение данных векторов, вычисляя определитель разложением по элементам 1-го столбца:

Найдем площадь искомого параллелограмма, вычислив модуль вектора :

.

Ответ: .

8. Составить уравнение прямой, проходящей через две точки М ₁(1,5), М ₂(3,3) и найти расстояние от точки Р (1,-2) до полученной прямой.

Решение:

Уравнение прямой, проходящей через две точки М ₁(х ₁, у ₁) и М ₂(х ₂, у ₂), записывается в виде:

.

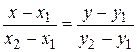В данном случае имеем , подставим эти значения в уравнение:

,

,

,

,

.

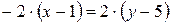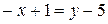Получили общее уравнение прямой, проходящей через две данные точки М ₁(1,5), М ₂(3,3).

Найдем расстояние от точки Р (1,-2) до полученной прямой.

Расстояние от точки Р (х ₀, у ₀) до прямой Ах+Ву+С =0 находится по формуле:

.

В данном случае 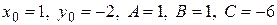. Подставляем эти значения в формулу:

.

Ответ: , .

9. Найти угол между прямыми:

.

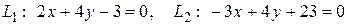Решение:

Угол между прямыми равен углу между их нормальными векторами.

Косинус угла между векторами можно вычислить по формуле:

,

где 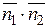- скалярное произведение векторов и ,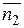

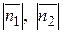- модули векторов и .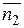

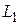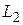Если прямая задана общим уравнением Ах+Ву+С =0, то ее нормальный вектор имеет координаты . Поэтому для прямой нормальный вектор будет иметь вид , для прямой нормальный вектор будет иметь вид .

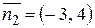Найдем скалярное произведение данных векторов в координатной форме:

.

Теперь вычислим модули данных векторов:

,

.

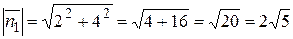Вычисляем косинус угла между нормальными векторами прямых:

.

Отсюда искомый угол между прямыми будет равен:

.

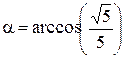Ответ: .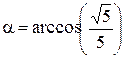

10. От общего уравнения прямой

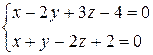
перейти к каноническому уравнению.

Решение:

Каноническое уравнение прямой имеет вид:

,

где - направляющий вектор данной прямой,

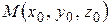- точка, принадлежащая прямой.

Направляющий вектор прямой 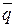– это вектор, параллельный данной прямой, поэтому он должен быть перпендикулярен нормальным векторам плоскостей, определяющих данную прямую, и 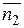. Тогда должно выполняться соотношение:

,

где - векторное произведение векторов и .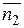

Найдем по уравнениям плоскостей координаты их нормальных векторов:

.

Найдем вектор :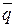

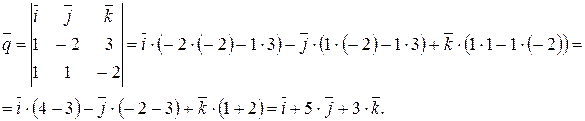
Поэтому вектор 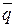имеет координаты .

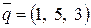В качестве точки 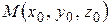, через которую проходит искомая прямая, можно взять точку пересечения ее с любой из координатных плоскостей, например с плоскостью Oyz. Так как при этом 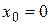, то координаты этой точки определятся из системы уравнений заданных плоскостей, если в них положить :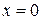

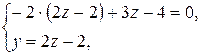
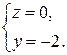
Получаем координаты точки .

Подставляем координаты точки М и направляющего вектора 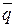в каноническое уравнение системы:

,

.

Ответ: .

11. Написать уравнение плоскости, проходящей через три заданные точки

.

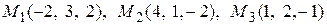Решение:

Уравнение плоскости, проходящей через точки , , , имеет вид:

.

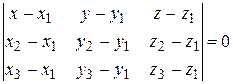Подставим координаты точек в уравнение:

,

.

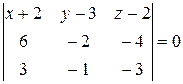Вычислим определитель слева разложением по элементам первой строки:

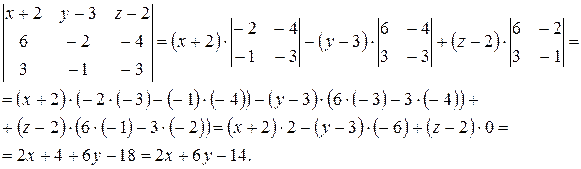
Получаем уравнение искомой плоскости:

,

.

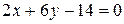Ответ: .

12. Найти расстояние от точки М до плоскости p:

.

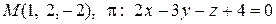Решение:

Расстояние от точки 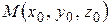до плоскости Ах+Ву+Сz+D =0 вычисляется по формуле:

.

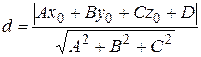В нашем случае . Подставляем эти значения в формулу и получаем:

.

Ответ: .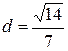

13. Найти проекцию точки М на плоскость p:

.

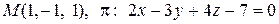Решение:

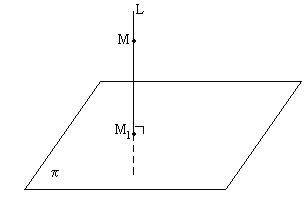
Составим уравнение прямой L, проходящей через точку M перпендикулярно плоскости p, тогда искомая проекция есть точка пересечения прямой 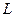и плоскости p.

Из общего уравнения плоскости определим нормальный вектор , он перпендикулярен плоскости и, значит, параллелен прямой L, т.е. является направляющим вектором для прямой L: .

Уравнение прямой, проходящей через точку 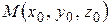и имеющей направляющий вектор имеет вид:

Дата добавления: 2017-01-13