Критерий серий

Критерий согласия Колмогорова.

Данный критерий позволяет осуществить проверку гипотез (15) в условиях, когда функция распределения 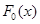модельного закона известна полностью, то есть не зависит от неизвестных параметров. Он основан на анализе мер уклонения эмпирической и модельной функций распределения.

Эмпирическая функция распределения по случайной выборке 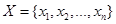реализаций СВ определяется по формуле:

.

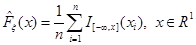Введём статистику

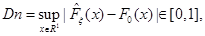
называемую расстоянием Колмогорова между 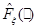и .

Известно, что гипотеза 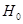верна и 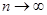(практически 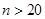), то статистика 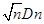имеет распределение Колмогорова с функцией распределения 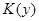вида:

.

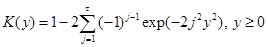Критерий согласия Колмогорова представляет собой следующее решающее правило:

принимается гипотеза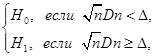

Порог 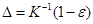- квантиль уровня 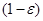распределения Колмогорова, - задаваемый пользователем уровень значимости.

В ППП СТАТМОД предполагается использование эквивалентной формы данного критерия вида (18), где .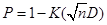

Критерий серий предназначен для проверки гипотезы о случайности выборки 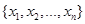. Критерий основан на исследовании знаковой последовательности разностей:

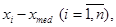(19)

где 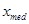- медиана выборки 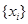. Знаковая последовательность состоит из знаков “+”, “-”, соответствующих разностям (19) и характеризуется:

1. общим числом серий ,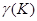

2. протяжённостью самой длинной среди 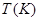, где 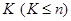- число элементов знаковой последовательности.

Под “серией” понимается последовательность подряд идущих одинаковых знаков.

Очевидно, если 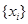- случайная выборка, то знаковая последовательность не должна содержать слишком длинных серий, а общее число серий не должно быть слишком малым.

В зависимости от величины К целесообразно использовать одно из следующих правил принятия решений.

Правило в случае К < 20.

Если хотя бы одно из неравенств:

,

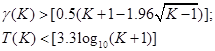(где [a] – целая часть числа а) оказывается нарушенным, то гипотеза о случайности выборки 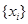отвергается с вероятностью ошибки .

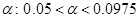Правило в случае К > 20 основано на использовании статистики:

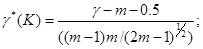(20)

где m – число наблюдений, меньших (больших) 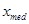. Известно, что статистика (20) распределена асимптотически (при К ® ¥) по стандартному нормальному закону. Отсюда правило принятия решения следующее: гипотеза о случайности выборки 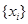принимается, если 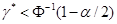и отвергается в противном случае (a - заданный уровень значимости).

Критерий “нисходящих” и ”восходящих” серий

Данный критерий позволяет обнаружить (с увеличением порядкового номера наблюдений) смещение среднего значения наблюдения как монотонного, так и более общего, например, циклического характера. Так же, как и в случае критерия серий, исследуется последовательность знаков разностей. Однако используется другая последовательность разностей: 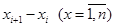, причём, если два или несколько следующих друг за другом наблюдения равны между собой, то принимается во внимание только одно из них.

Серия из плюсов называется “восходящей”, а серия из минусов - “нисходящей”, поскольку имеют место при возрастании и убывании наблюдений соответственно.

Критерий основывается на тех же принципах и статистиках 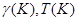, что и критерий серий.

Используется следующее решающее правило: если хотя бы одно из неравенств

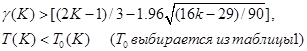
оказывается нарушенным, то гипотеза о случайности выборки 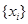отвергается с вероятностью ошибки .

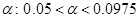Таблица 1: Зависимость от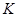

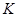
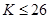
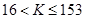
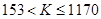
Дата добавления: 2017-02-01