
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вывод основного уравнения гидродинамики для турбулентного режима
|
|
|
|
(уравнения Рейнольдса)
 +
+  +
+  = 0 – уравнение неразрывности
= 0 – уравнение неразрывности
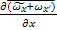 +
+  +
+ 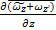 = 0
= 0
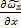 +
+ 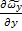 +
+  = 0 – уравнение неразрывности турбулентного течения
= 0 – уравнение неразрывности турбулентного течения
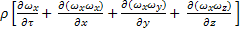 = -
= -  +
+ 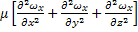
Уравнение Навье - Стокса
 =
=  +
+ 
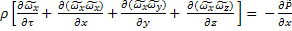 +
+ 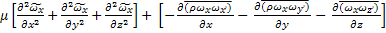
Приближение Буссинеска:
-
 =
=  =
= 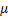 г
г
 -
-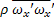
 =
= 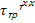 =
= 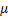 г
г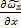 и т.д.
и т.д.
Тогда:
 =
=  (
( т)
т) – Уравнение Рейнольдса в приближении Буссинеска.
– Уравнение Рейнольдса в приближении Буссинеска.
 =
= 
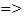 -
- 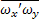 =
=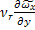
Параметры турбулентности:
L 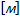 – масштаб турбулентности – расстояние в потоке, на котором средняя скорость изменяется на величину пульсационной составляющей.
– масштаб турбулентности – расстояние в потоке, на котором средняя скорость изменяется на величину пульсационной составляющей.
L = 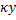 , константа Кармана
, константа Кармана 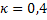 для крупномасштабных пульсаций
для крупномасштабных пульсаций
Изменение средней скорости на масштабе турбулентности 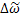
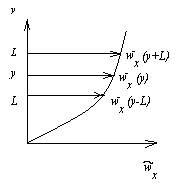
 = 1/2
= 1/2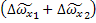 = L
= L =
=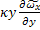 ,
,
Выражение получается взаимной подстановкой друг в друга приведенных ниже зависимостей.
 , так как разложение
, так как разложение  в ряд и ограничение его первым членом дает
в ряд и ограничение его первым членом дает
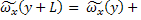 L
L
 =
= 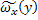 -
- 
 L
L , так как разложение
, так как разложение 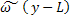 в ряд и ограничение его первым членом дает
в ряд и ограничение его первым членом дает
 L
L ,
,
ReL =  Rex =
Rex = 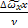 ,
,  - крупномасштабная пульсация, x мелкомасштабная пульсация и L
- крупномасштабная пульсация, x мелкомасштабная пульсация и L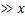 , таким образом диссипирует энергию мелкомасштабной пульсаци, так как малый критерий Re- это большая сила трения, большая вязкость, а, следовательно, большая величина диссипированной энергии.
, таким образом диссипирует энергию мелкомасштабной пульсаци, так как малый критерий Re- это большая сила трения, большая вязкость, а, следовательно, большая величина диссипированной энергии.
На основе теории размерности можно получить выражение для турбулентной вязкости:
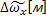 ; L
; L 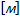 ;
; ;
;  – параметры потока, характеризующие течение:
– параметры потока, характеризующие течение:
 =
= 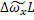 = L2
= L2 =
=  2y2
2y2
 т
т  =
= 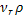 =
= 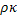 2y2
2y2
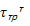 =
= 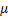 г
г 2y2
2y2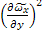
 = -
= -  2y2
2y2
После определения значений 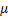 т и
т и  можно решать конкретные задачи с использованием уравнения Рейнольдса.
можно решать конкретные задачи с использованием уравнения Рейнольдса.
Определим профиль скоростей в плоском квазистационарном турбулентном потоке.
Определить профиль скоростей в плоском, квазистационарном, турбулентном потоке при безнапорном течении
 а) профиль скоростей, полученный решением уравнения Рейнольдса.
а) профиль скоростей, полученный решением уравнения Рейнольдса.
б)профиль скоростей в приближении пограничного слоя.
Из уравнения Рейнольдса при оговоренных условиях имеем:
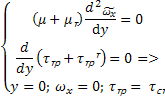
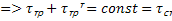
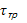 =
=  – слабо зависит от y.
– слабо зависит от y. 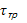 =
= 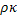 2
2 - пропорционально y2. Решаем методом асимптотического анализа со сращиванием полученных решений:
- пропорционально y2. Решаем методом асимптотического анализа со сращиванием полученных решений:
y ;
; 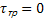 ;
; 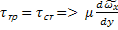 =
= 

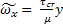 - линейная зависимость.
- линейная зависимость.
y ;
; 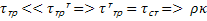 2
2
 Интегрируем и получаем:
Интегрируем и получаем:
 lny+ С – логарифмический профиль скоростей в потоке вдали от стенки
lny+ С – логарифмический профиль скоростей в потоке вдали от стенки
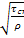 =
= 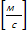 – назовем, согласно размерности динамической скоростью
– назовем, согласно размерности динамической скоростью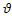 *
*
 =
=
 =
=
 *=
*= * - пульсационная составляющая и динамическая скорость – это одно и то же.
* - пульсационная составляющая и динамическая скорость – это одно и то же.
Re = 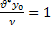 (при равном соотношении сил трения и инерции выбираем точку сращивания у, т.к. асимптотические решения получены для случаев превалирования силы трения (решение при у
(при равном соотношении сил трения и инерции выбираем точку сращивания у, т.к. асимптотические решения получены для случаев превалирования силы трения (решение при у или силы инерции (решение при у
или силы инерции (решение при у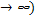 )
)
Координата сращивания равна:
у0=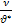
 у0=
у0=  =
=  =
= =
= 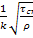 lny0+C
lny0+C  *-
*- lny0
lny0
Важный вывод: скорость в точке сращивания равна пульсационной составляющей  ,a
,a  - равна 0, что согласуется с гипотезой прилипания
- равна 0, что согласуется с гипотезой прилипания
 ln
ln +
+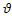 *=
*= 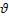 *
*
Точное решение этой задачи имеет вид:
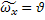 *
*
Полученные в результате решения уравнения Рейнольдса два различных вида профилей скоростей: линейного у стенки и логарифмического профиля скорости вдали от нее и вид соответствующих функций согласуется с гипотезой Прандтля о наличии в пристенной области пограничного слоя с иным, чем в ядре потока механизмом переноса количества движения.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 733; Нарушение авторских прав?; Мы поможем в написании вашей работы!