Частные и полный дифференциалы

Частным дифференциалом функции нескольких переменных по одной из независимых переменных называется главная часть соответствующего частного приращения, линейная относительно приращения рассматриваемой независимой переменной. Частный дифференциал функции нескольких переменных по одной из независимых переменных равен произведению соответствующей частной производной на приращение рассматриваемой независимой переменной. Дифференциал независимой переменной совпадает с ее приращением. Так для функции двух переменных 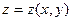частные дифференциалы

, .

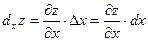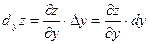Полным дифференциалом функции нескольких переменных называется главная часть полного приращения функции, линейная относительно приращений аргументов. Полный дифференциал функции равен сумме всех частных дифференциалов. Так

.

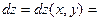
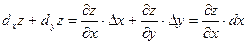
Функция, обладающая непрерывными частными производными, заведомо имеет полный дифференциал. Функция, имеющая полный дифференциал, называется дифференцируемой.

При достаточно малых 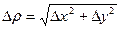, . Из последнего соотношения имеем следующий вид формулы применения дифференциала к приближенным вычислениям:

.

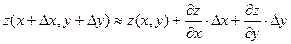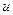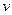
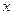Пусть и , , тогда через посредство промежуточных аргументов и - функция и 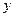. В этом случае полный дифференциал 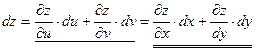. Из сравнения выражений подчеркнутых одной и двумя чертами, видим, что форма полного дифференциала не зависит от того, являются ли переменные, через которые выражается полный дифференциал, независимыми переменными или промежуточными аргументами. Такая независимость формы дифференциала от переменных дифференцирования называется инвариантностью полного дифференциала относительно переменных дифференцирования.

Дата добавления: 2014-01-14