Й учебный вопрос. Множественная нелинейная регрессия

Если связь между результативным признаком и анализируемы­ми факторами нелинейна, то выбранная для ее описания нелиней­ная многофакторная модель (степенная, показательная и т.д.):

Степенная - ;.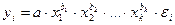

Экспонента – ;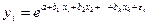

Гипербола – ;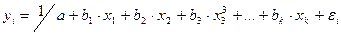

мо­жет быть сведена к линейной путем линеаризации.

Помимо уравнения линейной множественной регрессии в множественном регрессионном анализе может быть использовано соотношение (117)

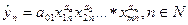
(117)

Логарифмируем левую и правую часть уравнения (117). В итоге получим

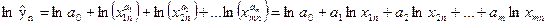
(118)

Неизвестные значения параметров ln a₀, a₁, a₂, … a_m, находятся с помощью метода наименьших квадратов. Значение параметра a₀ находится с помощью соотношения .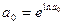

При наличии трех и более факторов достаточно сложно без наличия ПК и соответствующего программного продукта решать систему из четырех и, естественно, большего числа уравнений.

С учетом выше изложенного рассмотрим упрощенный и приближенный подход к определению значений параметров уравнении линейной множественной регрессии 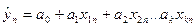. При этом будем считать, что все факторы, входящие в это уравнение, являются некоррелированы.

Данный подход решает указанную выше задачу в три этапа.

На первом этапе определяются приближенные значения параметров 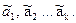для этого используются формулы (119)

(119)

Будем считать, что окончательные значения параметров a₁, a₂, … a_k с помощью соотношений (120)

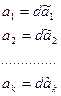
(120)

где d – неизвестное значение поправочного коэффициента.

Значение коэффициента d определяется с помощью метода наименьших квадратов, целевая функция которого имеет вид (121)

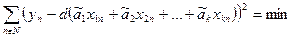
(121)

Аргументом данной функции 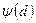является значение поправочного коэффициента d. Для того, чтобы его найти, необходимо продифференцировать функцию 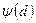по переменной d и полученное выражение приравнять нулю, в результате чего получим соотношение (122)

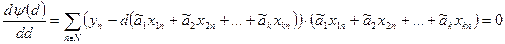
(122)

Значение поправочного коэффициента d находится по формуле

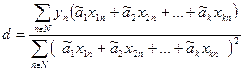
(123)

Далее находится значение параметра a₀. Для этого используется целевая функция (124)

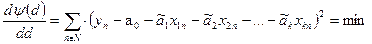
(124)

Данная функция 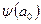зависит только от параметра а₀. Для того, чтобы найти значение этого параметра, необходимо продифференцировать функцию 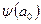по переменной а₀ и полученное выражение приравнять нулю. В итоге получим

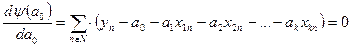
(125)

Тогда значение параметра а₀ определяется по формуле (126)

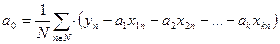
(126)

В общем случае можно предположить, что одному произвольно взятому значению независимой переменной Х соответствует некоторая совокупность значений зависимой переменной Y.

Пусть число случаев, когда одному и тому же значению независимой переменной Х соответствует некоторая совокупность значений зависимой переменной Y, равняется M. Для каждого m случая значению независимой переменной Х_m соответствует N_m совокупность зависимой переменной .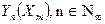

В этом случае для каждого значения 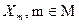, можно найти дисперсию зависимой переменной D(Y(X_m)). Для этого используется соотношение (126)

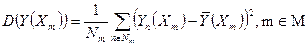
(127)

где

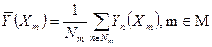
(128)

Возможны два варианта. Первый вариант характеризуется тем, что является справедливым соотношением (129)

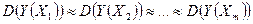
(129)

В этом случае можно говорить о гомоскедастичности зависимости зависимой переменной Y от независимой переменной Х.

Если же соотношение (129) не выполняется, то зависимость между независимой и зависимой переменной Х и Y является гетероскедастичной.

В последнем варианте вместо метода наименьших квадратов целесообразно использовать обобщенный метод наименьших квадратов.

Суть последнего из указанных выше методов заключается в следующем. Находится среднее значение дисперсии 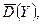для чего используется соотношение (130)

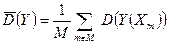
(130)

Далее определяются значения весовых коэффициентов K_m

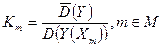
(131)

Предположим, что заданная функция, связывающая между собой значения независимой и зависимой переменной Х и Y имеет вид 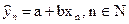. В этом случае целевая функция метода наименьших квадратов, используемого для определения неизвестных значений параметров a и b, имеет вид (132)

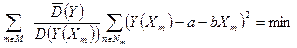
(132)

Обозначим эту функцию через 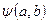. Тогда значения параметров a и b находятся в результате решения системы уравнений, включающих в себя уравнения (133) и (134)

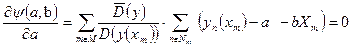
(133)

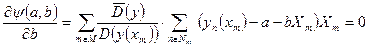
(134)

После использования метода наименьших квадратов необходимо проверить точность решения задачи, связанной с определением неизвестных значений параметров заданий функции.

Для этого находятся:

- значения остатков E_n, формуле (135)

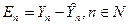
(135)

- среднеквадратичное значение остатков – по формуле (136)

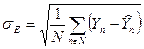
(136)

- среднее значение зависимой переменной Y – по формуле (137)

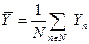
(137)

- процент ошибки, относящейся к среднему значению зависимой переменной Y – по формуле (138)

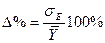
(138)

Кроме того, необходимо проверить коррелированность остатков 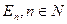. Для этого используется критерий Дарвина-Уотсона. Этот критерий связан с расчетом значения автокорреляции остатков по формуле (139)

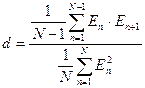
(139)

Если значение показателя d является незначительным, то это свидетельствует о том, что заданная функция регрессии выбрана правильно.

При исследовании экономических процессов нередко возникают ситуации, когда значение результирующего признака в текущий момент времени формируется под воздействием ряда факторов, действующих в прошлые моменты времени t-1, t-2 и т.д. Величину, характеризующую запаздывание в воздействии фактора на результат, называют лагом, а временные ряды самих факторов переменных, сдвинутые на один и более интервалов времени – лаговыми переменными.

В этом случае уравнение регрессии, если рассматривать независимую переменную Х и зависимую переменную Y, определяется соотношением (140)

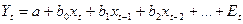
(140)

Наряду с лаговыми значениями независимых или факторных переменных на величину зависимой переменной текущего периода могут оказывать влияние ее значения в прошлые моменты или периоды времени. В этом случае может использоваться уравнение регрессии вида (141)

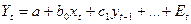
(141)

Для определения значений параметров уравнения (140) может быть использован метод, предложенный Койком. Последний предложил, что существует постоянный темп 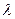(0<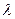<1) уменьшения во времени лаговых воздействий на результат.

Учитывая это обстоятельство, уравнение (140) приводится к виду (142)

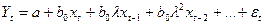
(142)

Запишем те же уравнения, только для момента времени t-1. в результате получим уравнение (143)

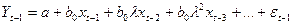
(143)

Умножим обе части уравнения (143) на l. В итоге получим

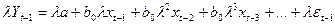
(144)

Вычтем соотношение (144) из соотношения (142), в результате чего получим

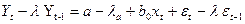
(145)

Пренебрежем значениями 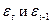. В итоге оценка переменной Y_t будет характеризоваться соотношением (146)

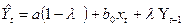
(146)

Введем обозначение

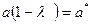
(147)

В этом случае уравнение (146)преобразуется к виду (148)

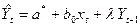
(148)

С помощью метода наименьших квадратов находятся неизвестные значения параметров a^*, b₀ и λ. Для этого используется целевая функция (149)

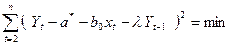
(149)

Обозначим 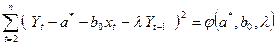. Значения a^*, b₀ и λ находятся в результате решения системы уравнений (150)

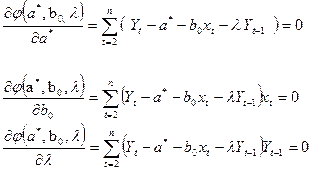
(150)

Задачу, связанную с определением значений параметров a^*, b₀ и λ, можно решать последовательно. В этом случае сначала используется целевая функция 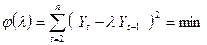. В этом случае λ находится из соотношения (151)

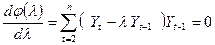
(151)

Далее для определения значения параметра b₀ используется целевая функция 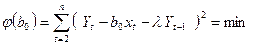. Значение параметра b₀ находится в результате решения уравнения (152)

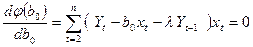
(152)

Для определения значения параметра a^* используется целевая функция 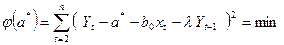. Значение данного параметра находится в результате решения уравнения (153)

(153)

Значение параметра a находится по формуле (153)

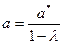
(154)

Значения параметров b₁, b₂, b₃ и т.д.находятся по формулам (155)-(157)

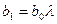
	(155)
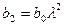
	(156)
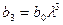
	(157)

и т.д.

При определении значений параметров уравнений (140) и (141) можно использовать также следующий подход. В соответствии с ним, если взять уравнение (140), определяются значения коэффициентов линейной парной корреляции 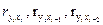и т.д. Если взять уравнение (141), то определяются значения коэффициентов линейной парной корреляции 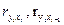и т.д.

Далее предполагается справедливость соотношений (158) для уравнения (140) и (159) для уравнения (141)

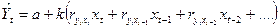
	(158)
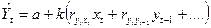
	(159)

где k – коэффициент, значение которого является неизвестным.

Значение данного коэффициента может быть найдено с помощью метода наименьших квадратов.

При решении данной задачи используется соотношение (160)

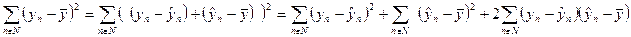
(160)

В данном выражении 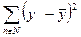характеризует собой величину общей дисперсии, выражение 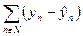- остаточной дисперсии, выражение 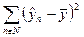- факторной дисперсии.

Выражение .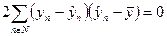

Это можно доказать следующим образом. Пусть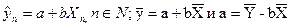

Тогда имеем:

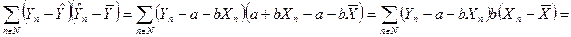
	(161)

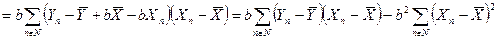
Известно, что

	(162)
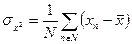
	(163)

из соотношения (162) находится формула (164)

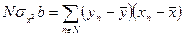
(164)

из соотношения (163) находится формула (165)

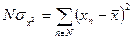
(165)

Подставим выражения (164) и (165) в соотношение (161). В итоге получим

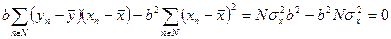
(166)

В результате является справедливым соотношение (167)

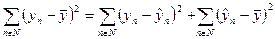
(167)

Выражение имеет N-1 степеней свободы.

Выражение 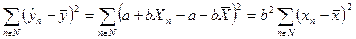имеет одну степень свободы. Число степеней свободы с левой и правой части выражения должно быть одинаковым. Исходя и этого выражение 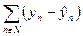имеет N-2 степеней свободы.

Находим общую, факторную и остаточную дисперсию, относящуюся на 1 степень свободы, используя формулу (168), (169) и (170)

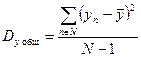
	(168)
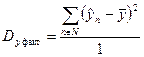
	(169)
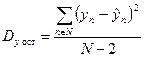
	(170)

Для оценки значимости статистических показателей используется F критерий, значение которого рассчитывается по формуле (171)

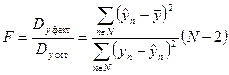
(171)

Найдем связь F критерия с коэффициентом детерминации r², где r – коэффициент линейной парной корреляции.

Для начала преобразуем выражение .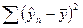

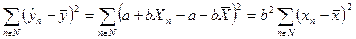
(172)

Являются справедливым соотношения

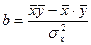
	(173)
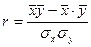
	(174)
	(175)
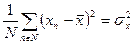
	(176)
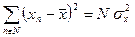
	(177)

В итоге получаем

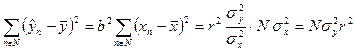
(178)

Далее преобразуем выражение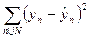

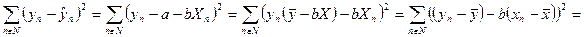
	(179)

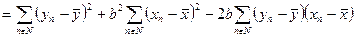
Являются справедливым выражения

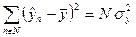
	(180)
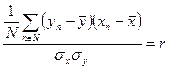
	(181)
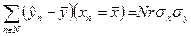
	(182)
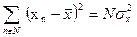
	(183)
	(184)

В результате выражение (179) преобразуется к виду (185)

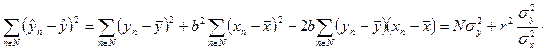
	(185)

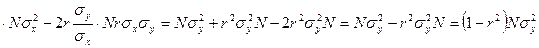
Подставим выражения (178) и (185) а соотношение (171). В результате получим

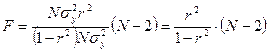
(186)

Для оценки значимости статистических показателей используется t – статистика (закон Стьюдента) и F – статистика (закон Фишера). t – статистика используется в предположении наличия линейных взаимосвязей, F – статистика – в предположении наличия нелинейных взаимосвязей.

t_r – статистика (ее расчетное значение) определяется по формуле (187)

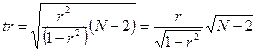
(187)

Она используется при оценке значимости коэффициента линейной парной корреляции r.

Для оценки значимости коэффициента линейной парной корреляции из таблицы t – распределения Стьюдента находится табличное значение 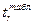. Для этого задается уровень значимости 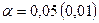и число степеней свободы m=N-2.

Если t_r > 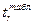, значение коэффициента линейной парной корреляции является значимым.

Для использования F – распределения вместо r² вводится R². Этот показатель показывает какая часть вариации зависимой переменной Y обусловлена вариацией ее факторной составляющей.

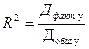
(188)

В этом случае преобразуется к виду

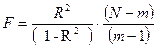
(189)

где m – число параметров уравнений регрессии (или число уравнений, необходимых для определения значений параметров).

Для оценки значимости статистических показателей с помощью распределения Фишера находится расчетное и табличное значение F – критерия (F_расч и F_табл). При определении табличного значения F – критерия задается 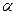- уровень значимости = и число степеней свободы k₁ = m-1 и k₂ = N-m.

Если F_расч > F_табл, это означает значимость определенных значений параметров регрессионной зависимости.

При m=2 формула (189) преобразуется у виду (190)

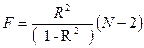
(190)

При m=3 формула (189) преобразуется к виду

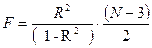
(191)

Помимо оценки значимости параметров линейной функции регрессии может определятся интервальная оценка данной функции.

Пусть

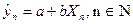
	(192)
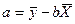
	(193)

Тогда имеем

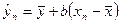
(194)

Возьмем дисперсию от левой и правой части выражения (194). В результате получим

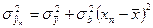
(195)

Найдем 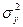. Оно определяется соотношением (195)

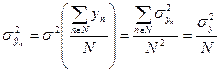
(196)

Значение параметра b может определяться с помощью соотношения (197)

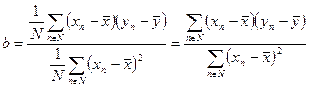
(197)

Тогда значение 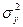может быть найдено по формуле (198)

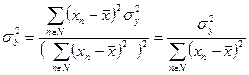
(198)

В итоге 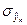определяется с помощью выражения (199)

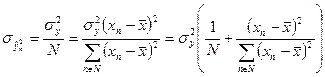
(199)

Предположим, что существует точное значение 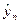, найденное не на основе выбора, а на основе генеральной совокупности. Обозначим это значение через M (Y_n).

Предполагается, что t статистика значения 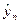определяется с помощью соотношения (200)

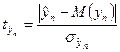
(200)

Значение 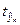- статистики находится по таблице распределения Стьюдента при числе степеней свободы N-2 и заданном значении вероятности 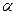=0,05 (0,01). Тогда доверительный интервал значения M (Y_n) определяется по формуле (201)

(201)

Для определения значения доверительного интервала математического ожидания случайной величины можно использовать формулу Чебышева, имеющую вид (202)

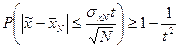
(202)

где 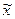- средняя по генеральной совокупности; 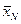- среднее значение по выборке объемом N; 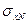- среднеквадратичное отклонение, найденное по выборке объемом n; t – неизвестное значение параметра, которое находится, используя формулу (203) при заданном значении вероятности (или доверительной вероятности) P.

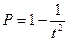
(203)

В итоге значение t определяется с помощью выражения (204)

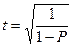
(204)

Доверительный интервал применительно к значению средней 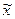находится по формуле (205)

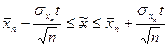
(205)

Если брать значение любого статистического показателя, то для определения его доверительного интервала можно использовать следующий подход.

В соответствии с ним из исходной совокупности объемом N случайным образом (с помощью метода Монте-Карло) формируется некоторая I совокупность выборок объемом M, при этом M<N. Далее по каждой выборке находится значение рассматриваемого показателя (например, коэффициент A линейной парной корреляции r_xyi), 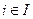. Далее находится среднеквадратичное отклонение данного показателя. Применительно к коэффициенту линейной парной корреляции среднеквадратичное отклонение 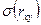находится по формуле (206)

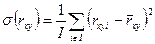
(206)

где

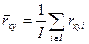
(207)

Используя эти значения (вместо 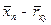, а вместо 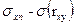) по формуле (205) определяется значение доверительного интервала значения коэффициента линейной парной корреляции.

Такой же подход может использоваться для определения доверительного интервала и для других статистических показателей.

Заключение — до 5 мин.

Содержание и методические рекомендации:

- обобщить наиболее важные, существенные вопросы лекции.

- сформулировать общие выводы.

- поставить задачи для самостоятельной работы.

- ответить на вопросы студентов.

Дата добавления: 2014-01-14