Техника и практика интегрирования

Метод интегрирования по частям применяется при вычислении ограниченного числа интегралов. С использованием этого метода интегрируются, как правило, обратные тригонометрические функции, логарифмические функции, произведения алгебраических выражений на тригонометрические, обратные тригонометрические, логарифмические и показательные функции. При достаточной практике интегрирования студенты без затруднений определяют, что данный интеграл вычисляется с помощью метода интегрирования по частям.

Основным методом интегрирования является метод замены переменных, с помощью которого находится преимущественное большинство интегралов. В отличие от практики дифференцирования функций, когда достаточно знать таблицу производных и понять технику дифференцирования функции от функции, практика интегрирования сложна тем, что каждый тип интеграла требует для решения своей собственной подстановки, поэтому необходимо ознакомиться со всеми типами решаемых интегралов. И если при дифференцировании функций теория и практика находятся в отношении 50% на 50%, то в интегрировании функций практика отыскания первообразных занимает до 80-90% времени освоения интегрального исчисления.

Вычисление неопределенных интегралов осложняется еще и тем, что первообразная не от всякой элементарной функции является элементарной функцией. Поскольку же мы знакомы в курсе только с элементарными функциями, то такие интегралы для нас точно (говорят в квадратурах) не вычисляются. Так не выражаются через элементарные функции следующие интегралы: , , , 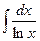. Однако, поскольку нужда в таких интегралах в приложениях математики имеется, то такие интегралы (первообразные функции) находятся и табулируются (составляются их таблицы). Так, например, хорошо изучена для нужд теории вероятности функция Гаусса - , и она табулирована при условии .

Дата добавления: 2014-01-14