Сферические функции

Сферическими функциями называют специальные функции одного переменного, являющиеся решениями дифференциальных уравнений, получающихся при применении метода разделения переменных для уравнения Лапласа, записанного в сферических координатах.

Рассмотрим сначала полиномы Лежандра – многочлены, имеющие вид . Очевидно, что 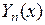– многочлен степени 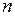. Покажем, что этот многочлен удовлетворяет дифференциальному уравнению , которое можно записать в виде .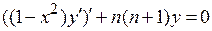

Для доказательства воспользуемся формулой Лейбница для получения производной -го порядка от произведения двух функций 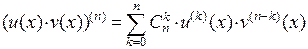, где 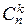– число сочетаний из 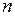по 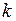, причем 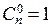. В соответствии с этой формулой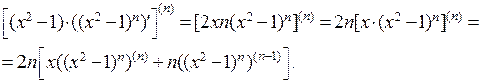

С другой стороны, по той же формуле Лейбница

Сравнивая правые части полученных выражений, имеем

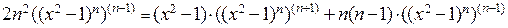
или

.

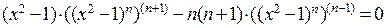Остается продифференцировать обе части последнего выражения и умножить обе части на 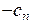, чтобы получить

.

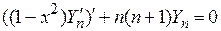Заметим, что дифференциальное уравнение

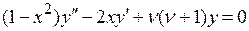
имеет ограниченное в окрестности точек 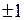решение тогда и только тогда, когда 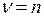– натуральное число.

Если положить 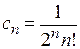, то получим из 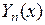полином Лежандра

,

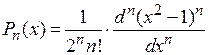обладающий свойством Согласно сказанному полином Лежандра удовлетворяет дифференциальному уравнению

.

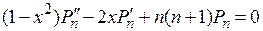Примером сферической функции является 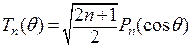, удовлетворяющая уравнению

.

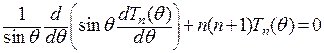П р и м е р. Выяснить, при каких значениях числа 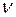можно получить ограниченное решение 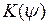дифференциального уравнения

и найти это решение.

Введем новое переменное 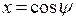и обозначим 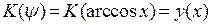. При этом 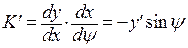, 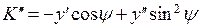. Теперь исходное дифференциальное уравнение совпадает с уравнением 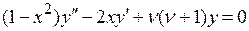, которое имеет ограниченное решение только если 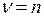, где 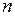– любое натуральное число. В этом случае 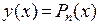, и значит, .

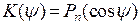Свойство ортогональности полиномов Лежандра. Покажем, что 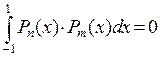, если 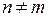. Поскольку при разных параметрах один параметр всегда меньше другого, положим 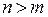. Теперь, применяя 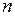раз интегрирование по частям, получим

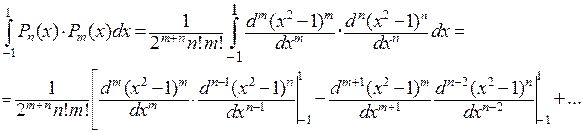
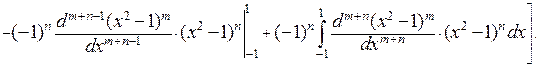
Все слагаемые в квадратной скобке, кроме последнего – нули из-за содержащихся в них сомножителей 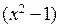в положительных степенях, а последнее – ноль из-за того, что содержащаяся под интегралом производная 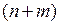-го порядка от многочлена степени 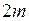равна нулю. Следовательно, равенство 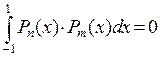, , 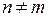доказано.

Это равенство называется условием ортогональности множества полиномов Лежандра на отрезке .

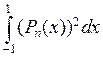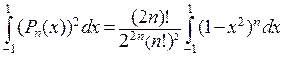Нетрудно сосчитать и значение , применяя то же интегрирование по частям раз. Мы получим . Последний интеграл вычисляется сведением к B-функции заменой 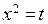. При этом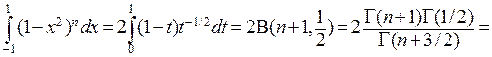

.

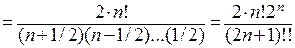Подставляя в предыдущую формулу, получим .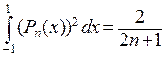

Дата добавления: 2014-01-14