Изоэнтропийное течение совершенного газа

Будем рассматривать газ, подчиняющийся уравнению Клапейрона – Менделеева: 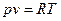или 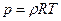, теплоемкости, в частности изобарную теплоемкость, считаем не зависящими от температуры (постоянными): .

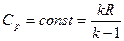Под изоэнтропийным движением, как правило, понимается адиабатное движение без трения. Возможно рассматривать и изоэнтропийное течение с трением: трение увеличивает энтропию, тогда в процессе движения нужно предусмотреть какой – либо способ уменьшения энтропии, например охлаждать газ. Если прирост энтропии за счет трения полностью компенсируется ее уменьшением за счет охлаждения, получим изоэнтропийное течение с трением, но такое течение не будет адиабатным.

Условимся рассматривать такое изоэнтропийное течение, которое является обратимым (без трения) адиабатным; внутреннюю энергию и энтальпию будем считать функциями только температуры: , , поскольку газ совершенный (в общем случае , 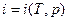для реальных газов и жидкостей).

Необходимо составить математическую модель течения.

Запишем три закона сохранения для стационарного адиабатного течения совершенного газа.

Закон сохранения энергии в дифференциальном виде:

(1)

или, интегрально: .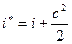

Уравнение Бернулли:

(2)

В уравнении (2) пренебрегли изменением потенциальной энергии в поле земного тяготения, что вполне допустимо для газа; справа стоит ноль, поскольку считаем течение адиабатным в широком смысле: к потоку не подводится теплота и механическая работа.

Уравнение неразрывности также запишем в дифференциальной форме, прологарифмировав, а затем продифференцировав (эта операция называется логарифмическим дифференцированием):

,

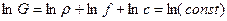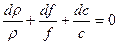(3)

Зададимся вопросом: достаточно ли этих трех уравнений?

Для того, чтобы систему уравнений можно было решить, число неизвестных должно быть равно числу уравнений. Кроме того, для решения необходимо задать граничные, а в случае нестационарного течения еще и начальные условия. Все задачи делятся на прямые и обратные. Прямая постановка означает, что заранее известны геометрические границы течения (например, в случае течения в канале – форма стенок), на этих границах и ставятся граничные условия. В обратных задачах форма границ течения неизвестна, ее надо найти (например, подобрать такую форму крылового профиля, которая обеспечивала бы минимальные потери на вязкое трение и максимальную подъемную силу). Обратные задачи всегда сложнее в решении.

Будем поэтому рассматривать прямую задачу. В одномерной постановке это означает, что площадь канала считается заданной, так что не входит в число переменных, закон ее изменения известен.

В уравнениях (1) – (3) неизвестных величин четыре: , а уравнений три!

Связь плотности и давления задается условием баротропности 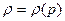, но мы пока не знаем, какова эта связь (мы «авансом» написали заголовок, но пока не показали, что наше адиабатное без трения течение является изоэнтропийным).

- три параметра, характеризующие термодинамическое состояние системы, свойства рабочего тела. Из курса термодинамики известно, что для описания простого рабочего тела (простого вещества, без фазовых превращений, химических реакций и т.д.) необходимо и достаточно двух параметров. Другие параметры могут быть определены по этим двум. Так, если определять температуру по давлению и плотности, то связь этих трех параметров образует т.н. термическое уравнение состояния .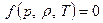

Простейшим термическим уравнением состояния является уравнение Клапейрона – Менделеева: .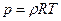

Совершим над этим уравнением операцию логарифмического дифференцирования:

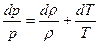(4)

Написали недостающее четвертое уравнение, но при этом появилась пятая неизвестная – температура.

Для замыкания системы запишем т.н. калорическое уравнение состояния, использовав определение изобарной теплоемкости:

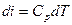(5)

Калорическими называются уравнения состояния, в которые входят величины, содержащие в своей размерности Дж - 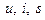и др. Раньше вместо джоуля использовали калорию, отсюда и название.

Итак, мы составили математическую модель задачи для описания одномерного стационарного адиабатного (без подвода теплоты и механической работы) течения, записав пять уравнений для пяти неизвестных величин (в случае пространственного движения уравнений было бы семь, т.к. уравнение Бернулли писалось бы в трех проекциях).

Из (1) и (2) уравнений имеем:

.

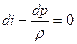Используем объединенную форму записи I и II начал термодинамики для обратимого процесса:

или .

Следовательно, 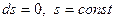- адиабатное течение без трения является изоэнтропийным!

Теперь можем записать условие баротропности:

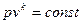или .

Введем понятие скорости звука (будем обозначать 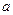) и числа Маха ().

Газы (сжимаемые жидкости) – это упругая среда, по которой могут распространяться волны сжатия и разрежения. Звуковая волна является малым возмущением, сильным возмущением в газе, например, в воздухе, будет взрыв или гром. В курсе общей физики было показано, что скорость распространения малого возмущения (скорость звука) в сжимаемой среде .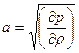

Ньютон полагал, что процесс распространения звуковой волны является изотермическим. Но вычисленная изотермическая скорость звука 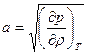оказалась заметно (на 20%) меньше экспериментальной.

Поскольку звуковая волна распространяется с достаточно большой скоростью, и теплообмен с окружающей средой практически не успевает происходить, процесс распространения звуковой волны можно с достаточной точностью считать адиабатным. В нашем случае – обратимым адиабатным, т.е. изоэнтропийным: .

,

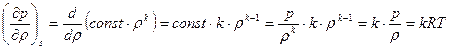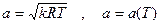- для совершенного газа скорость звука зависит от температуры (и от сорта газа, т.е. от показателя адиабаты). Очень высока скорость звука у гелия He: молярная масса мала, 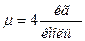, индивидуальная газовая постоянная велика , к тому же показатель адиабаты у инертных газов максимально высокий: .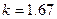

При течении сжимаемого потока возможны две ситуации:

1) 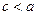- дозвуковое течение,

2) - сверхзвуковое течение.

Здесь 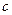- скорость частиц, скорость газового потока, 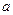- скорость звука, измеренная в том же месте, где и 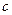, т.н. местная скорость звука.

Число Маха – это безразмерная скорость, отношение скорости потока к местной скорости звука: .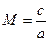

В дозвуковом течении , в сверхзвуковом - .

Число Маха относится к критериям подобия, как и число Рейнольдса. Если 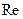характеризует силы трения (вязкости), то характеризует сжимаемость потока. В несжимаемой среде 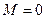, т.к. скорость звуковой волны в несжимаемой среде бесконечно велика: .

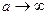Покажем, что число Маха характеризует сжимаемость течения.

В уравнении Бернулли (2) первое слагаемое умножим и разделим на и выделим скорость звука:

(*)

Поскольку дифференциал – это приращение, изменение величины, то в числителе стоит относительное изменение плотности, а в знаменателе – относительное изменение скорости, квадрат числа Маха характеризует соотношение между относительными изменениями плотности и скорости.

При плотность меняется меньше, чем скорость; при плотность меняется сильнее скорости.

Если 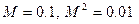, то относительное изменение плотности составляет 1% от относительного изменения скорости. Поэтому при малых сжимаемостью можно пренебречь, даже если речь идет о течении газового потока.

Критерий Маха точнее можно назвать критерием изоэнтропийной сжимаемости.

Переход от к резко меняет картину течения.

Путь вдоль направления равномерно и прямолинейно движется частица бесконечно малого размера и при движении создает в окружающем газе малые возмущения (малые, поскольку она сама мала). В момент времени частица достигла положения «О».

Рассмотрим сначала дозвуковое течение, (рис.9-3).

Повернем процесс вспять. Секунду назад частица находилась в положении «1». При равномерном и прямолинейном движении расстояние равно произведению скорости на время, но время 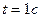, так что расстояние численно равно скорости частицы. Секунду назад, находясь в положении «1», частица испустила звуковую волну, которая распространяется со скоростью 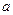(сфера радиуса 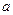). Аналогичные рассуждения – для момента времени 2 секунды назад и т.д.

Вывод: при дозвуковом движении возмущение обгоняет частицу, предыдущее возмущение движется впереди последующего. Наблюдатель узнает о приближении частицы по звуку, предшествующему появлению частицы (если не учитывать затухание звука из – за трения).

Совершенно иная картина наблюдается при сверхзвуковом движении частицы (рис.9-4).

Частица движется быстрее, чем звуковая волна, обгоняет создаваемые своим движением возмущения. Все возмущения при этом попадают в конусообразную зону. Этот конус называется конусом Маха, угол 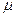- углом Маха. За пределами конуса Маха находится зона невозмущенного течения, которую часто называют зоной молчания. Наблюдатель (человечек, изображенный на рисунке 9-4), услышит звук, когда образующая конуса Маха пройдет через (*).

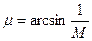(см. рис.9-5).

Образующая конуса, разграничивающая зону молчания и зону возмущения, носит двойное название:

1) линия Маха (или линия малого возмущения);

2) характеристика.

Дата добавления: 2014-01-14