
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Для уравнения Пуассона
|
|
|
|
ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ ПРИ РЕШЕНИИ ЗАДАЧ ОБ ИЗГИБЕ БАЛКИ И ДИРИХЛЕ
Лекция №9
Рассмотрим два примера применения МКЭ
































 1. Изгиб балки м
1. Изгиб балки м
z

 М
М
 |
 y
y 
v1 v2 v3 v4 vn+1



 F F F F F
F F F F F
z1 z2 zi …. zi+1 zn+1
Определить прогиб опорной балки, подверженной действию постоянного изгибающего момента М, когда жесткость сечения балки Е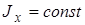 . Изгиб описывается дифференциальным уравнением
. Изгиб описывается дифференциальным уравнением
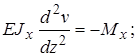
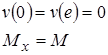 (1) Cтатически определенная
(1) Cтатически определенная
система.
Соответствующая вариационная формулировка (потенциальная энергия) для (1) имеет вид:
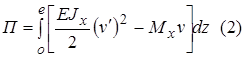
1) Балку разобьем на  конечных элементов
конечных элементов
zi i 2) В качестве аппроксимирующих (коорди-









 натных) функций для КЭ возьмем миним.
натных) функций для КЭ возьмем миним.
vi+1 функции. 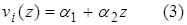 . Система
. Система
 vi
vi 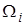 имеет только одну степень свободы в каждом
имеет только одну степень свободы в каждом
zi+1–zi= Δz узле – прогиб (в общем случае имеется прогиб
и угол поворота сечения). Коэффициенты 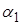 и
и 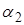 определим через неизвестные прогибы
определим через неизвестные прогибы 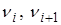 (определяется матрица функции формы):
(определяется матрица функции формы):
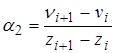
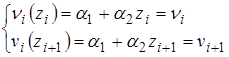
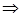 (4)
(4) 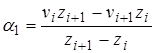
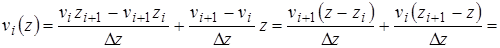 (3¢)
(3¢)
= 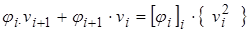 - координатная функция
- координатная функция 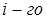 КЭ, которая содержит 2 неизвестных параметра
КЭ, которая содержит 2 неизвестных параметра  .
.
Причем, 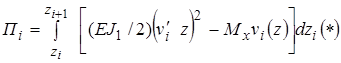 Из условия
Из условия
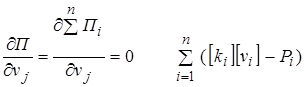 -
-
можно составить матрицу жесткости 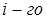 момента
момента 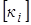 .
.
3) Определение кусочно-непрерывной функции для всей области:
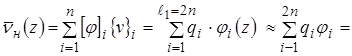
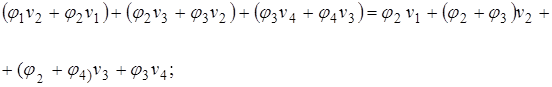 (5)
(5)
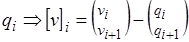 ;
; 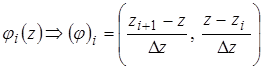 ~
~ 
При этом необходимо учитывать граничные условия.
В данном случае 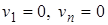 ;
; 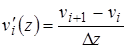 по (3¢)
по (3¢)
4) Составление разрешающей системы уравнений из условия
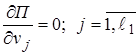 ;
; 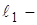 общее количество степеней свободы (число неизвестных
общее количество степеней свободы (число неизвестных 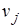 ).
).
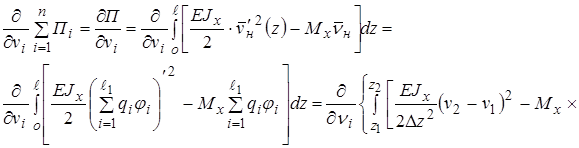
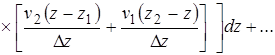 (6)
(6)
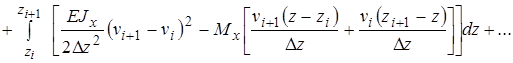
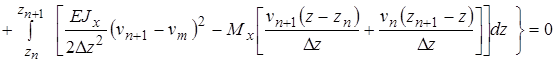
Пусть 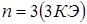 . Тогда
. Тогда 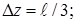
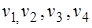 - неизвестные.
- неизвестные.
1 2 3 Тогда (6) 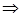
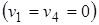 :
:






1 2 3 4
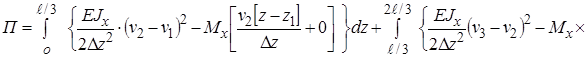

-
– 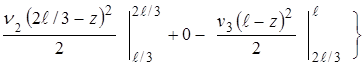 (6¢)
(6¢)
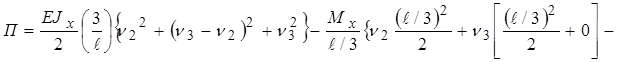
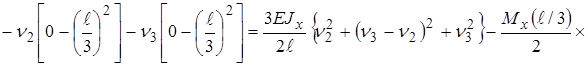
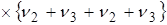 ;
;



















 5)
5)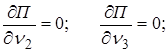 Система двух линейных алгебраических уравнений
Система двух линейных алгебраических уравнений 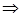
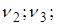
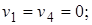 тогда
тогда
z1 z2 z3 z4
v2 v3
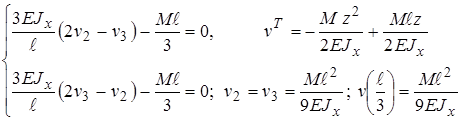
6) Далее можно определить другие характеристики: 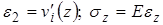 .
.
В общем случае П=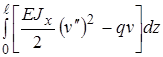 и необходимо минимизировать этот функционал. При этом координатные функции можно выбрать в виде
и необходимо минимизировать этот функционал. При этом координатные функции можно выбрать в виде
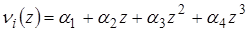
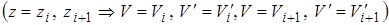 или
или 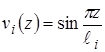
2) Задача Дирихле для уравнения Пуассона (на примере кручения стержня некругового сечения)
Рассмотрим задачу Дирихле для уравнения Пуассона (на примере кручения прямолинейного стержня): 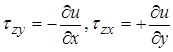 .
.
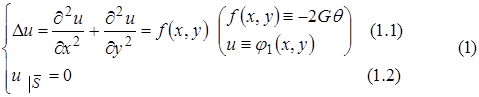
Вариационная формулировка задачи (1) имеет вид:
 (2¢)
(2¢)
Задачу (2¢) запишем в виде:
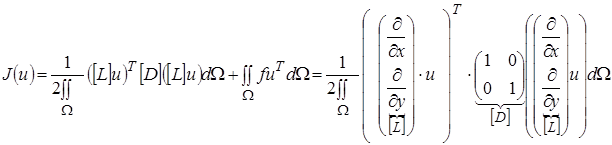 -
-
–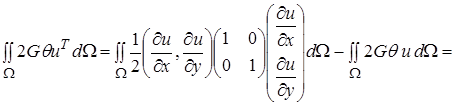
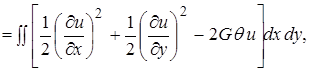 т.е. функционал (2¢) записан в виде, требуемом в МКЭ.
т.е. функционал (2¢) записан в виде, требуемом в МКЭ.
Приступим к реализации МКЭ для решения задачи (1).
1) Пусть область 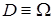 (сечение стержня) квадрат. В силу наличия четырех осей симметрии можно рассматривать только 1/8 квадрата.
(сечение стержня) квадрат. В силу наличия четырех осей симметрии можно рассматривать только 1/8 квадрата.





 6
6



 y
y

 (4) 0,25см
(4) 0,25см



 4 5
4 5

 (3)
(3)
(1) 0,25см






 (2)
(2)
1 см 1 0,25см 2 0,25см 3 х
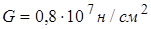 ;
;  . Область разобьем на четыре треугольника КЭ, проведем нумерацию элементов и узлов
. Область разобьем на четыре треугольника КЭ, проведем нумерацию элементов и узлов 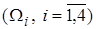 .
.
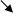


 2) В качестве аппроксимирующих (координатных) функций для j-го конечного элемента
2) В качестве аппроксимирующих (координатных) функций для j-го конечного элемента 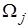 возьмем линейные аппроксимации:
возьмем линейные аппроксимации: 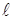
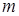

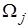

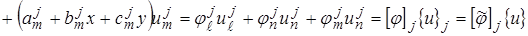 , (4)
, (4)
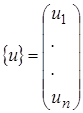 где коэффициенты
где коэффициенты 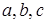 вычисляются по известным координатам узлов
вычисляются по известным координатам узлов  КЭ;
КЭ; 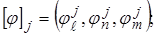
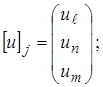 j=
j=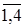 .
.
3) Аппроксимирующая кусочно-непрерывная функция для всей области:
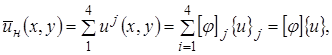 (5)
(5)
где 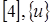 строятся
строятся 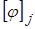 и
и 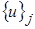
4) Составим разрешающую систему уравнений из условия 
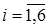
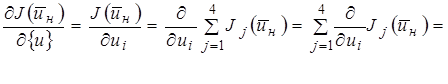
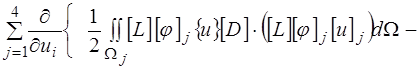
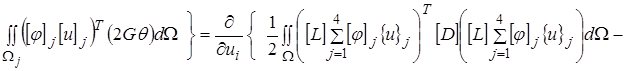
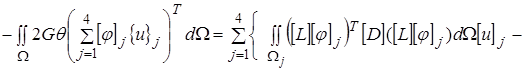
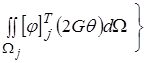 =0 (6)
=0 (6)
Обозначим 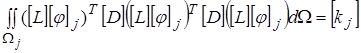 (7.1)
(7.1)
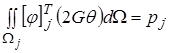 - вектор столбец (7.2)
- вектор столбец (7.2)
Тогда 
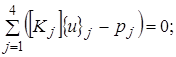 (8)
(8)
где 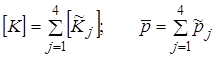 , знак
, знак  ~ означает запись соответствующих расширенных матриц для всех узловых значений.
~ означает запись соответствующих расширенных матриц для всех узловых значений.
Здесь следует отметить, что глобальная матрица узловых значений искомых величин 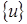 в каждом КЭ
в каждом КЭ 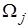 содержит
содержит 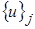 . Аппроксимация для каждого КЭ
. Аппроксимация для каждого КЭ 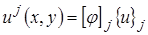 может быть также записана в виде
может быть также записана в виде
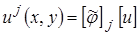 , где компоненты
, где компоненты 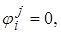 если
если 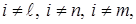 т.е. если не содержит элементов матрицы функции формы из j-го КЭ.
т.е. если не содержит элементов матрицы функции формы из j-го КЭ.
В соответствии в вышеизложенным запишем интерполяционные полиномы для КЭ:

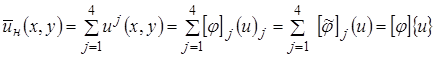 (9)
(9)
Построим матрицы жесткости для 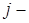 го элементов
го элементов 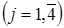
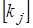 :
:
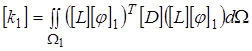 . В нашем случае матрица характеристик (матрица упругости)
. В нашем случае матрица характеристик (матрица упругости) 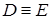 - единичная матрица.
- единичная матрица.
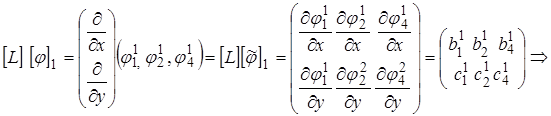
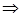
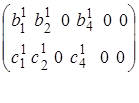
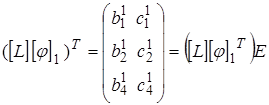 ;
;  -постоянные величины (10)
-постоянные величины (10)
Вычислим коэффициенты 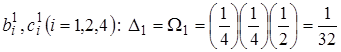
 ;
; 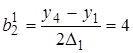 ;
; 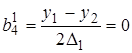 ;
;
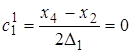 ;
; 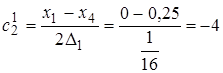 ;
; 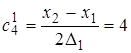 (11)
(11)
Итак, по (10) 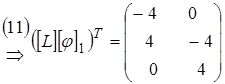 или
или 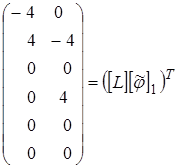 (12)
(12)
Тогда 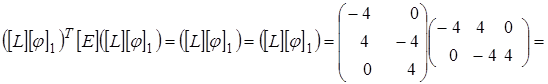
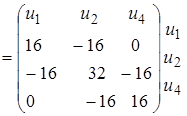 или
или 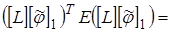
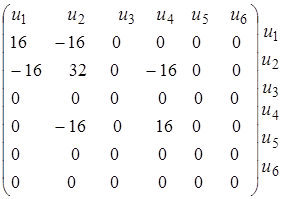 (13)
(13)
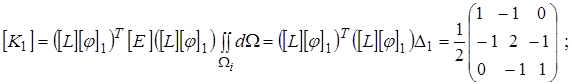 или
или
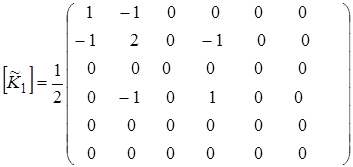 ;
; 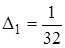 (14)
(14)
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 651; Нарушение авторских прав?; Мы поможем в написании вашей работы!