Предельные теоремы

Интегральная предельная теорема Муавра-Лапласа послужила источником большого цикла исследований, имеющих фундаментальное значение для теории вероятностей и ее приложений. Для того, чтобы составить представление о направлении этих исследований, запишем теорему Муавра-Лапласа в виде

(*)

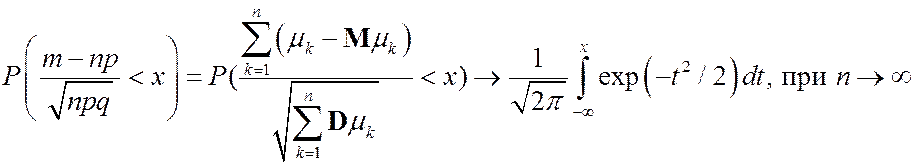Таким образом, теорема может быть сформулирована в виде:

Вероятность того, что сумма уклонений независимых с.в. 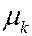, принимающих 2 значения 0 и 1 с вероятностями q и p =1- q от их МО, деленная на корень квадратный из суммы дисперсий слагаемых будет меньше x, при числе слагаемых стремящемся к бесконечности, стремиться к интегралу .

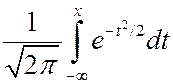Возникает вопрос: насколько тесно связано соотношение (*) со специальным выбором слагаемых 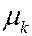, не будет ли оно иметь место и при более слабых ограничениях, наложенных на функции распределения слагаемых.

Итак, возникает следующая задача:

дана последовательность независимых с.в. 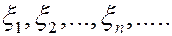с МО а_k и дисперсиями .

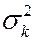Спрашивается, какие условия нужно наложить на величины 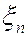, чтобы функции распределения сумм

сходились к стандартному нормальному закону распределения?

Ответом на данный вопрос являются приведенные ниже теоремы.

Теорема (Линдеберга-Леви)

Пусть 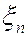- независимые, одинаково распределенные случайные величины с м.о. а и дисперсией 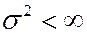. Тогда последовательность функций распределения нормированных сумм

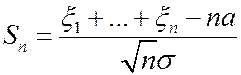
слабо сходится к стандартному нормальному распределению, т.е.

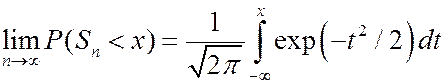
Доказательство.

Для х.ф. случайной величины x с конечными м.о. и дисперсией имеет место следующее разложение

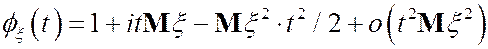
Действительно, при любом фиксированном x имеем .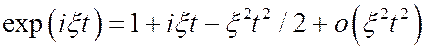

Взяв МО от обеих частей последнего равенства, получим приведенное разложение.

Запишем нормированную сумму в виде

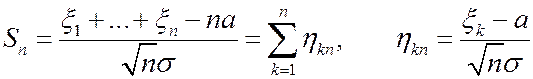
Поскольку 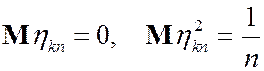, то x.ф. случайной величины 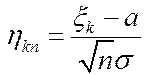имеет вид:

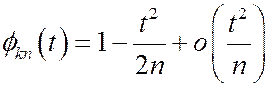
Х.ф. величины S_n имеет вид:

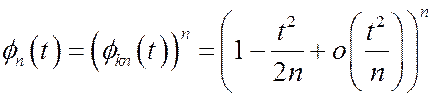
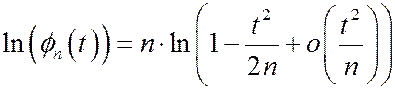
Для любого 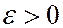при любом ограниченном t, 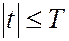всегда можно выбрать n, такое что

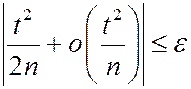. Поэтому .

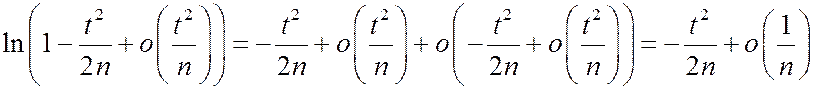При этом

.

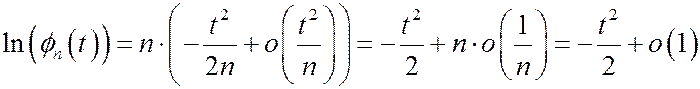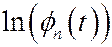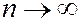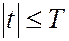Т.О. сходится при к равномерно по t (). Поэтому

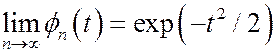и имеет место слабая сходимость функций распределения нормированных сумм к стандартному нормальному распределению.

Задача 1.

Складываются 10000 чисел, каждое из которых округлено до 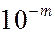. Ошибки округления независимы и равномерно распределены в интервале .

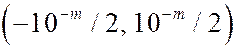Найти пределы, в которых с вероятностью 0.99 лежит суммарная ошибка.

Дата добавления: 2014-01-14