Повний двійковий суматор

Робота повного двійкового суматора описується наступною таблицею істинності (табл.2).

Таблиця 2

Ci

b

a

S

Co

К-карта для S

К-карта для Co

Склейки

*11

1*1

11*

Рис. 1

Логічні рівняння для повного двійкового суматора

Рівняння складені за таблицею істинності:

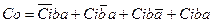, . (1)

Виконаємо спрощення рівнянь (1). Рівняння для суми виразимо через функцію додавання за модулем 2, а рівняння для переносу спростимо двома способами: методом К-карт (рис. 1, друга формула в (2)) і на основі властивостей логічних функцій (друга формула в (3)).

, ; (2)

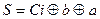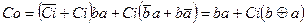; . (3)

2.1. Програма реалізації повного двійкового суматора мовою AHDL з використанням логічних операторів або логічних символів (формули (1))

Використання логічних операторів	Використання логічних символів
SUBDESIGN sm_1 (a,b,Ci:INPUT; S,Co:OUTPUT;) BEGIN S=NOT Ci AND NOT b AND A OR NOT Ci AND b AND NOT A OR Ci AND NOT b AND NOT A OR Ci AND b AND A; Co=NOT Ci AND b AND a OR Ci AND NOT b AND a OR Ci AND b AND NOT a OR Ci AND b AND a; END;	SUBDESIGN sm_1 (a,b,Ci:INPUT; S,Co:OUTPUT;) BEGIN S=! Ci &! b & A #! Ci & b &! A # Ci &! b &! A # Ci & b & A; Co=! Ci & b & a # Ci &! b & a # Ci & b &! a # Ci & b & a; END;

Символ повного двійкового суматора

Результати моделювання

2.2. Схемна реалізація повного двійкового суматора в середовищі MAX+PLUS II на основі формул (1).

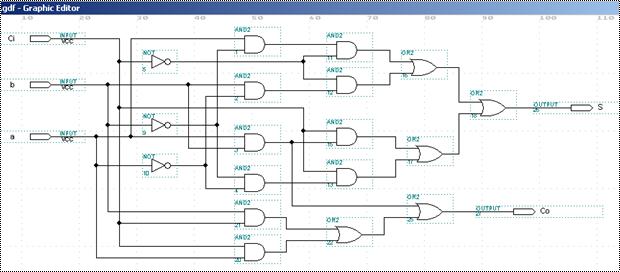
Результати моделювання

2.3. Програми реалізації повного суматора мовою AHDL за спрощеними логічними формулами (2) з використанням логічних операторів та логічних символів.

Використання логічних операторів	Використання логічних символів
SUBDESIGN sm_2 (a,b,Ci:INPUT; S,Co:OUTPUT;) BEGIN S=Ci XOR b XOR a; Co= b AND a OR Ci AND b OR Ci AND a; END;	SUBDESIGN sm_2 (a,b,Ci:INPUT; S,Co:OUTPUT;) BEGIN S=Ci $ b $ a; Co= b & a # Ci & b # Ci & a); END;

Результати моделювання

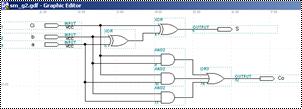
Схемна реалізація повного суматора за спрощеними формулами (2) в середовищі MAX+PLUS II.

2.3. Програми реалізації повного суматора мовою AHDL за спрощеними логічними формулами (3) з використанням логічних операторів та логічних символів.

Використання логічних операторів	Використання логічних символів
SUBDESIGN sm_3 (a,b,Ci:INPUT; S,Co:OUTPUT;) BEGIN S=Ci XOR b XOR a; Co= b AND a OR Ci AND (b XOR a); END;	SUBDESIGN sm_3 (a,b,Ci:INPUT; S,Co:OUTPUT;) BEGIN S=Ci $ b $ a; Co= b & a # Ci & (b $ a); END;

Результати моделювання

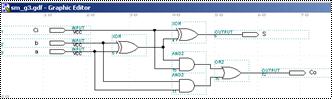
2.4. Схемна реалізація повного суматора за спрощеними формулами (3) в середовищі MAX+PLUS II.

2.5. Програмна реалізація повного суматора мовою AHDL з використанням таблиці істинності (табл. 2)

SUBDESIGN sm_4

(a,b,Ci:INPUT;

S,Co:OUTPUT;)

BEGIN

TABLE

Ci,b,a=>S,Co;

0,0,0=>0,0;

0,0,1=>1,0;

0,1,0=>1,0;

0,1,1=>0,1;

1,0,0=>1,0;

1,0,1=>0,1;

1,1,0=>0,1;

1,1,1=>1,1;

END TABLE;

END;

Результати моделювання

2.6. Схемна реалізація повного двійкового суматора з використанням символу напівсуматора (hsm) і елемента OR2.

Результати моделювання

3. Схемна реалізація трирозрядного двійкового суматора з використанням символів напівсуматора (hsm) і повного двійкового суматора (sm_1)

Результати моделювання

4. N-розрядний параметризований двійковий суматор

Суматор даного типу ― комбінаційний пристрій, що виконує операцію арифметичного додавання двох N-розрядних двійкових чисел a[], b[] і вхідного коду переносу Сі. Нижче наведено опис такого суматора на вентильному рівні.

Примітив CARRY явно вказує компілятору на необхідність використання схеми ланцюгового переносу логічного елемента НВІС сімейства FLEX. При розміщені НВІС сімейства МАХ компілятор ігнорує примітив CARRY.

PARAMETERS (N=7);

SUBDESIGN sm_Nr_p

(a[N..0], b[N..0], Ci: INPUT;

S[N..0], Co: OUTPUT;)

VARIABLE

C[N+1..0]:NODE;

BEGIN

C[0]=Ci;

FOR i IN 0 TO N GENERATE

S[i]=a[i]$b[i]$C[i];

C[i+1]=CARRY(a[i]&b[i]#C[i]&(a[i]#b[i]));

END GENERATE;

Co=C[N+1];

END;

Результати моделювання при

Результати моделювання при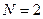

5. Восьмирозрядний двійковий суматор, реалізований на основі операції додавання шин.

SUBDESIGN add_8r

(

A[7..0],B[7..0],Ci:INPUT;

S[7..0],Co:OUTPUT;

)

BEGIN

(Co,S[])=(B"0",A[])+(B"0",B[])+(B"00000000",Ci);

END;

Результати моделювання

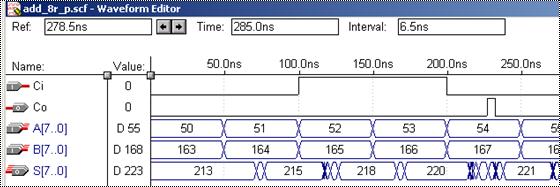
5. N-розрядний параметризований двійковий суматор, реалізований на основі операції додавання шин.

PARAMETERS (N=7);

SUBDESIGN add_8r_p

(

A[N..0],B[N..0],Ci:INPUT;

S[N..0],Co:OUTPUT;

)

VARIABLE

zero[N..0]:NODE;

BEGIN

zero[]=0;

(Co,S[])=(B"0",A[])+(B"0",B[])+(zero[],Ci);

END;

6. Перетворення прямого коду в обернений і навпаки

Параметризована програма переведення прямого коду в обернений.

PARAMETERS (N=7);

SUBDESIGN Pr_ob_1

(

A[N+1..0]:INPUT;

B[N+1..0]:OUTPUT;

)

BEGIN

IF A[N+1]==VCC

THEN

B[N+1]=VCC;

B[N..0]=!A[N..0];

ELSE

B[]=A[];

END IF;

END;

7. Перетворення прямого коду в доповняльний і навпаки

Параметризована програма переведення восьмирозрядного прямого коду в доповняльний.

PARAMETERS (N=7);

SUBDESIGN Pr_dop_1

(

A[N+1..0]:INPUT;

B[N+1..0]:OUTPUT;

)

BEGIN

IF A[N+1]==VCC

THEN

B[N+1]=VCC;

B[N..0]=!A[N..0]+B"00000001";

ELSE

B[]=A[];

END IF;

END;

8. Восьмирозрядний двійковий віднімач, побудований з використанням доповняльного коду

PARAMETERS (N=7);

SUBDESIGN sub_8r_1

(

A[N+1..0], B[N+1..0]:INPUT;

Sp[N+1..0], Sg, Sd[N+1..0]:OUTPUT;

)

VARIABLE

R[N+1..0],Co:NODE;

BEGIN

(Co, R[])=(B"0",A[])+(B"0",!B[])+B"0000000001";

IF R[N+1]==B"1" THEN

Sg=B"1";

Sp[]=!R[]+B"000000001";

Sp[N+1]=B"1";

ELSE

Sg=B"0";

Sp[]=R[];

END IF;

Sd[]=R[];

END;

Результати моделювання

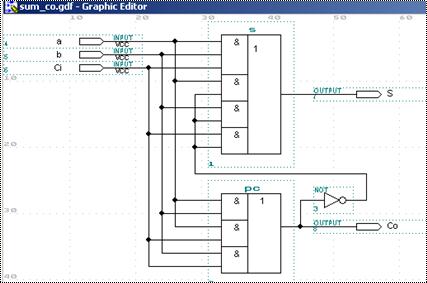
9. Восьмирозрядний двійковий віднімач, реалізований на основі операції віднімання

PARAMETERS (N=7);

SUBDESIGN sub_8r_p

(

A[N..0],B[N..0],Ci:INPUT;

S[N..0],Co:OUTPUT;

)

VARIABLE

zero[N..0]:NODE;

BEGIN

zero[]=0;

(Co,S[])=(B"0",A[])-(B"0",B[])+(zero[],Ci);

END;

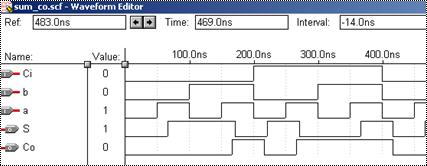
10. Повний двійковий суматор мовою AHDL з використанням напівсуматорів і вузлів типу NODE (два варіанти)

SUBDESIGN hsm_2

(a,b,Ci:INPUT;

S,Co:OUTPUT;)

VARIABLE

S1,Co1,Co2:NODE;

BEGIN

Co1=a&b;

S1=!a&b#a&!b;

S=!Ci&S1#Ci&!S1;

Co2=Ci&S1;

Co=Co1#Co2;

END;

Результати моделювання

SUBDESIGN hsm_22

(a,b,Ci:INPUT;

S,Co:OUTPUT;)

VARIABLE

S1,Co1,Co2:NODE;

BEGIN

Co1=a&b;

S1=a$b;

S=Ci$S1;

Co2=Ci&S1;

Co=Co1#Co2;

END;

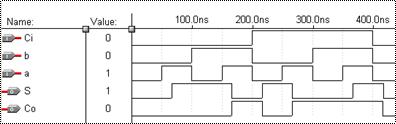
Результати моделювання

Дата добавления: 2014-01-11