Собственный момент ядра J (спин)

Выше отмечалось, что целочисленные значения J появляются для орбитального момента количества движения, который имеет классический аналог, а полуцелые значения характерны для спина, который классического не имеет. Однако существуют частицы, как с целым, так и с полуцелым спином. Примерами частиц с целым спином являются фотон и пион, в то время как электроны, нуклоны обладают спином ½. Не говорит ли такое различие спинов о каком-то глубоком различии между самими частицами? Это на самом деле так и есть: оба класса частиц ведут себя в сходных физических ситуациях совершенно по-разному. Для этого рассмотрим, например, систему из двух тождественных частиц, которые, в свою очередь, обозначим цифрами 1 и 2. Частицы имеют одинаковые спины J, но ориентации этих спинов 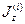у них могут быть разными. Волновая функция такой системы имеет вид

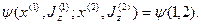
Если две частицы поменять местами, то волновая функция системы будет равна y (2,1). Замечательным фактом является то, что волновые функции тождественных частиц являются либо симметричными, либо антисимметричными при перестановках 1«2:

y (1,2) =+y (2,1) симметричная

y (1,2) =-y (2,1) антисимметричная

Существует глубокая связь между спином и симметрией волновых функций, впервые указанная Паули и доказанная им с помощью релятивистской квантовой теории. Волновая функция системы n тождественных частиц с полуцелым спином, называемых фермионами, меняет знак, если переставить в ней любые две частицы. Волновая функция системы n тождественных частиц с целым спином, называемых бозонами, остаётся неизменной при перестановке в ней любых двух частиц.

Связь между спином и симметрией приводит к так называемому принципу Паули. Предположим, что две частицы обладают в точности одними и теми же квантовыми числами. Тогда говорят, что данные две частицы находятся в одном и том же состоянии. Перестановка 1«2 оставит волновую функцию двух частиц неизменной. Однако, если обе частицы являются фермионами, то волновая функция должна изменить знак и поэтому должна обратиться в нуль. Следовательно, можно говорить о принципе запрета, который гласит, что одно квантовомеханическое состояние может занять только один фермион.

Дата добавления: 2014-01-14