Поверхностные инт. 2 рода

Определение и вычисление. Пусть E гл. поверхность и MÎE, нормалью к E в т. M наз. единичный вектор ^ касат. пл. в т. M. Стороной E наз. непр. поле нормалей, т.е. правило, которое с " MÎE связывает нормаль в этой т., причем координаты нормали являются непр. фун. точки поверхности. Если у поверхности $ сторона, то $ еще одна сторона, противоположная, и поверхность наз. двусторонней, поверхность наз. ориентированной, если указана одна из его сторон. Пусть 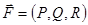непр. ВП на гл. поверхность E и 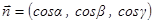сторона E, поверхностным интегралом 2-го рода наз. число

,

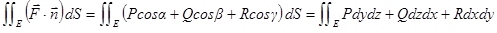где последнее выражение служит обозначением.

Часто инт. 2-го рода наз. потоком ВП.

Преобразуем поверхностный интеграл, пусть гл. поверхность задана уравнением 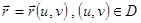, берем сторону 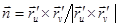, тогда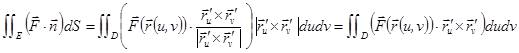

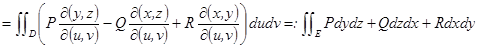
Рассмотрим случай, когда E – верхняя сторона графика фун. , :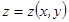

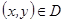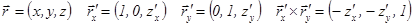
Þ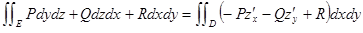

Частный случай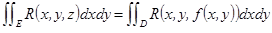

Пример ,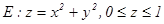

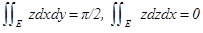
Свойства

1. При переходе к противоположной стороне инт. меняет знак: поток в сторону 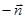равен минус потоку в сторону .

2. Аддитивность. Если гл. поверхность E разделена кусочно-гладкой кривой на две части 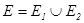, тогда .

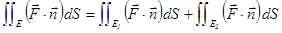Дополним опред.: пусть E кусочно-гладкая поверхность, т.е. состоит из конечного числа гл. участков, 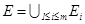, и их стороны согласованы на ребрах соединения, тогда по опред. положим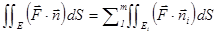

Формула Гаусса-Остроградского

1. Определение div. Пусть 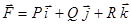гл. ВП, фун 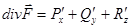наз. дивергенцией поля 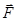. Пример: 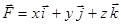– поле радиуса вектора, тогда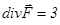

2. Теорема. Пусть область 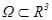ограничена кусочно-гладкой поверхностью E, 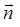– внешняя сторона E, и 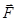гл. ВП на множестве 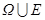, тогда ,

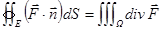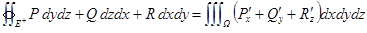
Пр.: поток радиуса вектора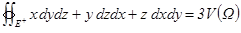

Формула Стокса

1 Определение rot. Пусть 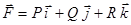- гл. ВП в области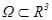

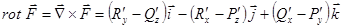
Пр.: поле скоростей цилиндра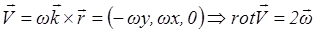

2 Сторона и край поверхности. Пусть E гл. незамкнутая поверхность, 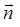– сторона E, 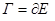– край E, 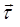– направление Γ; 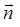и 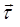согласованы если они подчиняются правилу правой руки.

3 Теорема. Пусть 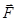гл. ВП в области Ω, 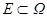, тогда ,

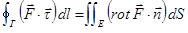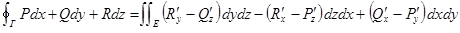
Формула Ньютона-Лейбница

1. Определение grad. Пусть u – гл. фун, .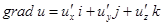

2. Теорема. Если u – гл. фун в области 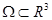, Γ – гл. кривая в области Ω,

соединяющая точки A и B, 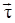– направление на Γ от A к B, тогда ,

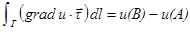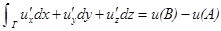
Дата добавления: 2014-01-14