Ряды распределения

Результаты сводки и группировки оформляются в виде статистических рядов распределения.

Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку.

Они характеризуют состав (структуру) изучаемого явления, позволяют судить об однородности совокупности.

Ряды распределения, образованные по качественным признакам, называются атрибутивными (должность, профессия). При группировке ряда по количественному признаку получают вариационные ряды. При этом вариационные ряды по способу построения бывают:

Ø дискретными (прерывными)

Ø интервальными (непрерывными).

Вариационные ряды состоят из двух элементов: варианты и частоты.

Варианта - это отдельное значение варьируемого признака, которое он принимает в ряду распределения.

Частотами называют численности отдельных вариант или каждой группы вариационного ряда.

Частоты, выраженные в долях единицы или в процентах к итогу, называются частностями. Сумма частот составляет объем ряда распределения.

Пример дискретного ряда распределения.

Таблица 4

Дискретный ряд распределения

Число товарных секций	На 01.01.2006	На 01.01.2007
Число магазинов	в % к итогу	Число магазинов	в % к итогу
Итого

Удобнее всего ряды распределения анализировать при помощи графического изображения. Характер распределения изображается графически в виде полигона распределения.

Х – число секций; У – число магазинов (%).

Для его построения в прямоугольной системе координат на оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении абсцисс и ординат точки соединяются прямыми линиями, в результате чего получают ломаную линию, называемую полигоном частот.

На оси ординат могут наноситься не только значения частот, но и частностей вариационного ряда.

Интервальный ряд распределения так же, как и дискретный, помогает выявить структуру изучаемого явления.

Пример интервального ряда распределения.

Таблица 5

Интервальный ряд распределения

Выработка рабочих, тыс. руб.	Число рабочих, чел.	% к итогу	Кумулятивная (накопленная) численность рабочих, чел.
80-100
100-120			15 (5 + 10)
120-140			35 (15 + 20)
140-160			45 (35 + 10)
160-180			50 (45 + 5)
итого

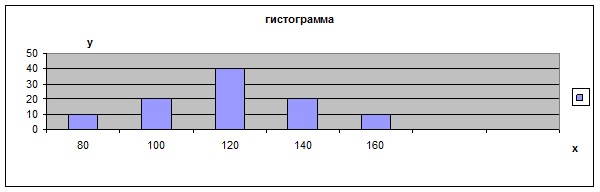
Интервальный ряд распределения изображается графически в виде гистограммы. При ее построении на оси абсцисс откладываются величины интервалов ряда, высота которых равна частотам, отложенным на оси ординат. Над осью абсцисс строятся прямоугольники, площадь которых соответствует величинам произведений интервалов на их частоты.

Гистограмма - график, на котором ряд распределения изображается в виде смежных друг с другом столбиков.

Гистограмма может быть преобразована в полигон распределения, если найти середины сторон прямоугольников и соединить эти точки прямыми линиями, как показано на рисунке.

Х – выработка рабочих; У – число рабочих (%).

В практике экономической работы часто возникает потребность в преобразовании рядов распределения в кумулятивные ряды, строящиеся по накопленным частотам.

Накопленные частоты определяются путем последовательного прибавления к частотам (или частностям) первой группы показателей последующих групп ряда распределения.

Для графического изображения ряда накопленных частот используется кумулятивная кривая. Кумуляты наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов, т.е. в точках 100, 120, 140, 160, 180. длина этих линий равна величине накопленных частот в конкретном интервале. Соединяя затем эти перпендикуляры, получаем ломаную линию, от начала ряда до той точки, которая равна объему данной совокупности, т.е. сумме частот.

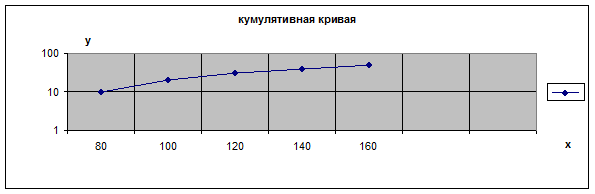
Если при графическом изображении вариационного ряда в виде кумуляты оси поменять масштабами, то мы получим огиву.

При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах. Это необходимо для устранения влияния величины интервала на распределение и дает возможность сравнивать частоты.

В подобных случаях для обеспечения необходимой сравнимости исчисляют плотность распределения, т.е. определяют, сколько единиц в каждой группе приходится на единицу величины интервала.

Таблица 6

Распределение организаций по размеру товарооборота

Группы организаций по размеру товарооборота, млн. руб.	Число организаций	Величина интервала	Плотность распределения единиц
До 50			0,5 (25/50)
50-120			0,65
120-250			0,5 (65/130)
250-450			0,4
450-980			0,04

Сравнение частот отдельных групп показывает, что чаще всего встречаются организации с интервалом 250-450 (80). Расчет плотности распределения вносит в это поправку и дает более точную характеристику распределения магазинов по товарообороту.

Разновидностью кумулятивной кривой является график Лоренца. Он используется для характеристики процессов концентрации, дифференциации, специализации и т.д.

Например, необходимо дать характеристику уровня концентрации производства в промышленности по числу рабочих.

Группировка сельскохозяйственных организаций предприятий по численности рабочих (в % к итогу).

Таблица 7

Распределение организаций по числу рабочих

Группа организаций по числу рабочих, чел.	Число предприятий	Среднегодовая численность
% к итогу	Накопленные (кумулятивные) итоги	% к итогу	Накопленные (кумулятивные) итоги
До 100	35,0	35,0	3,3	3,3
101-200	19,6	54,6	5,4	8,7
201-500	22,9	77,5	14,2	22,9
501-1000	11,3	88,8	15,3	38,2
1001-3000	8,4	97,2	26,8	65,0
3001-10000	2,5	99,7	23,6	88,6
1001 и более	0,3		11,9

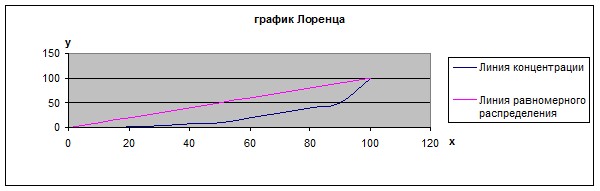
Для построения графика Лоренца исчислим накопленные (кумулятивные) итоги числа предприятий и среднегодовой численности рабочих. Построим квадрат 100х100, по оси абсцисс отложим накопленные итоги единиц совокупности, а по оси ординат – накопленные итоги объема явления.

Соединив соответствующие накопленным итогам точки плавной кривой, получим график Лоренца.

Если бы численность рабочих распределялась равномерно по числу предприятий, т.е. процесс концентрации отсутствовал полностью, график представлял бы собой прямую линию по диагонали квадрата. При неравномерном распределении численности рабочих по числу предприятий линия концентрации отходит от прямой линии и представляет собой вогнутую кривую, причем чем выше уровень концентрации, тем дальше отходит линия Лоренца от линии равномерного распределения, тем больше ее кривизна.

Для измерения концентрации разработаны специальные показатели – уровни концентрации.

Х – Единицы совокупности;

У – Объем явлений.

Для получения обобщенной, комплексной характеристики социально-экономического явления используются не отдельные показатели, а система статистических показателей, которая предусматривает исчисление абсолютных, относительных и средних величин.

Дата добавления: 2014-01-14