Найбільше та найменше значення функції в замкненій області

Для відшукання найбільшого та найменшого значень функції в замкненій області D, що позначаються відповідно , необхідно знайти екстремальні значення функції в точках, що лежать всередині області D та на її границі, та обрати з них найбільше та найменше.

Приклади 3. 1) Знайти найбільше та найменше значення функції 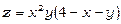у трикутнику, обмеженому лініями х =0, у =0, х+у =6.

Знайдемо стаціонарні точки даної функції, використовуючи необхідні умови екстремуму:

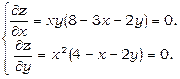
Оскільки всередині області 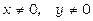, то

Таким чином, стаціонарною точкою буде М ₁(2,1). Значення функції в цій точці

Тепер проведемо дослідження на границі області D. На прямій х+у =6 змінна у= 6 -х, функція z набуває вигляду

Знайдемо найбільше та найменше значення цієї функції на відрізку 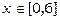. Для цього скористаємось необхідною умовою екстремуму функції однієї змінної: . Після розв’язання цього рівняння знайдемо х ₁=0, х ₂=4. Знайдемо значення функції в цих точках та на кінцях відрізку: z (0)=0, z (4)=-64, z (6)=0.

На прямій у =0 маємо z =0.

Отже, задана функція z має найбільше значення в точці М ₁(2,1) всередині області, найменше значення – в точці М ₂(4,2) на границі області: .

2) Знайти найбільше та найменше значення функції в крузі .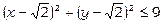

Тут розглядається область D, обмежена колом 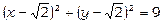, включаючи і точки кола.

Знайдемо стаціонарні точки даної функції: маємо 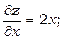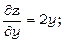в силу необхідних умов екстремуму знаходимо х =0, у =0.

Нескладно бачити, що в точці (0,0) функція має найменше значення z =0, причому вказана точка є внутрішньою точкою області D.

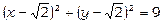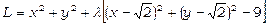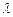Дослідимо на умовний екстремум функцію , якщо х та у пов’язані співвідношенням . Розглянемо функцію . Знайдемо частинні похідні Для визначення х, у та отримаємо систему рівнянь

Ця система має два розв’язки: х=у=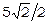, та z =25; x=y=, та z =1. Значить, найбільшого значення функція набуває в точці 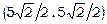. Таким чином, .

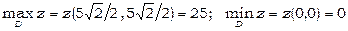Дата добавления: 2014-01-15