
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
V. Підведення підсумків заняття
|
|
|
|
ІV. Узагальнення та систематизація знань
План
ІІІ. Виклад нового матеріалу
І. Організаційний момент
Хід заняття
Лекція 14
Тема: Нормальний закон розподілу
Мета: Ознайомити студентів з нормальним законом розподілу та формулами знаходження числових характеристик при нормальному розподілі.
Література
1. Соколенко О. І. Вища математика. Підручник. К.: Академія, 2002.
2. Литвін І.І. та інш. Вища математика. Навчальний курс. Л.: Глобус, 2002.
3. Овчинников П.П. Вища математика. Ч.2. – К.: Техніка, 2004.
а) готовність групи до заняття;
б) перевірка присутніх.
ІІ. Актуалізація опорних знань студентів
а) повідомлення теми та мети заняття;
б) відповіді на запитання раніше вивчених лекцій.
1. Нормальний закон розподілу
VІ. Домашнє завдання: вивчити матеріал лекції.
Зміст лекції
Серед розподілів неперервних випадкових величин центральне місце займає нормальний (закон Гаусса). Він часто застосовується в задачах практики, проявляється в тих випадках, коли випадкова величина Х є результатом дії великого числа факторів, кожний з яких окремо на величину Х впливає мало і не можна виділити, який більше, а який менше.
Основна особливість, що виділяє нормальний закон серед інших, полягає в тому, що він є граничним законом, до якого наближаються інші закони розподілу.
Означення. Нормальним називається розподіл ймовірностей неперервної випадкової величини, якщо її густина розподілу має вигляд:
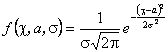 (1)
(1)
для довільного значення  і довільних чисел
і довільних чисел 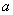 і
і  .
.
Числа 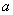 і
і  називають параметрами розподілу і мають певний ймовірнісний зміст, який розглянемо нижче.
називають параметрами розподілу і мають певний ймовірнісний зміст, який розглянемо нижче.
Графіком функції (1) є крива, яку в літературі називають кривою Гаусса, або нормальною кривою.
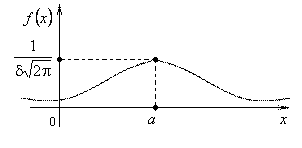

Якщо у формулі (1) покласти 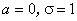 , отримуємо нормовану функцію Гаусса, яка нам уже траплялася в теоремах Муавра-Лапласа під назвою функції Лапласа.
, отримуємо нормовану функцію Гаусса, яка нам уже траплялася в теоремах Муавра-Лапласа під назвою функції Лапласа.
Бачимо, що нормальний розподіл визначається двома параметрами: 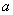 і
і  . Досить знати ці параметри, щоб задати нормальний закон розподілу. Доведемо, що ймовірнісний зміст цих параметрів наступний:
. Досить знати ці параметри, щоб задати нормальний закон розподілу. Доведемо, що ймовірнісний зміст цих параметрів наступний: 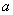 - математичне сподівання, а
- математичне сподівання, а  - середнє квадратичне відхилення.
- середнє квадратичне відхилення.
Дійсно: 
Перший доданок  , бо функція непарна, а інтегрування ведеться в межах, симетричних відносно початку координат; другий доданок
, бо функція непарна, а інтегрування ведеться в межах, симетричних відносно початку координат; другий доданок 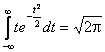 - інтеграл Пуассона, отже:
- інтеграл Пуассона, отже:
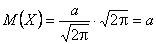 . (2)
. (2)


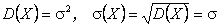 . (3)
. (3)
Відмітимо деякі властивості нормальної кривої:
а) крива симетрична відносно прямої  і
і 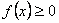 ;
;
б) крива має один максимум при  , бо
, бо 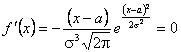 при
при  ,
,  при
при 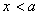 і
і 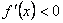
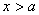 , при
, при 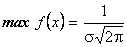 ;
;
в) крива асимптотично наближається до осі 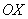 , бо
, бо  ;
;
г) зміна математичного сподівання 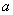 при
при  призводить до зміщення кривої Гаусса вздовж осі
призводить до зміщення кривої Гаусса вздовж осі 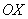 .
.
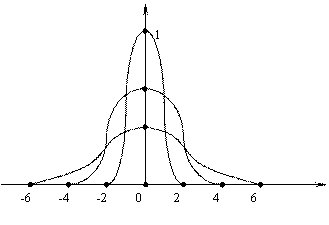
При зміні середнього квадратичного відхилення 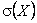 і
і  крива розподілу міняє свій вигляд (див рис.1), де крива І відповідає
крива розподілу міняє свій вигляд (див рис.1), де крива І відповідає 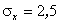 , крива ІІ -
, крива ІІ - 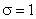 , а для кривої ІІІ -
, а для кривої ІІІ - 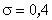 ,
, 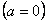 .
.

|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 610; Нарушение авторских прав?; Мы поможем в написании вашей работы!