Замечание 2. Функция имеет экстремум только в критических точках

Достаточное условие экстремума.

Пусть функция определена в критической точке x₀ и дифференцируема в некоторой окрестности этой точки, за исключением, может быть, самой x₀. Если «при переходе» через точку x₀ слева направо производная меняет знак с плюса на минус, то x₀ – точка максимума; с минуса на плюс – точка минимума.

Доказательство:

Пусть производная меняет знак с «+» на «-».

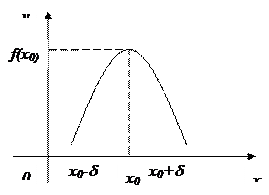Тогда слева от х₀, т.е. на (х₀-δ,х₀) .

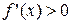Þ слева от х₀ функция 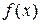возрастает.

Справа от х₀, т.е. на (х_0, х₀+δ) .

Þ справа от х₀ функция 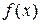убывает.

Т.о. в окрестности точки х₀ выполняется

неравенство .

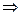х₀ – точка локального максимума.

Аналогично доказывается для минимума.

Ч.т.д.

Пример: Исследовать функцию на монотонность и найти точки экстремума.

а) .

1. Область определения функции D(y)=R.

2. .

Критические точки: 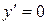. 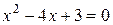Þ , .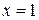

x	(-∞;1)	x=1	(1;3)	x=3	(3;+∞)
	+		–		+
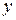
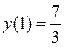
	возрастает	max	убывает	min y(3)=1	возрастает

б) .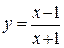

1. Область определения функции D(y): x¹-1.

2. ;

.

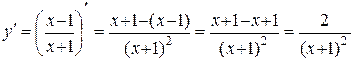Критические точки: 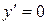, т.е. числитель равен нулю Þ нет точек;

– не существует, т.е. знаменатель равен нулю Þ.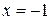

x	(-∞;-1)	x=-1	(-1;+∞)
	+	не существует	+
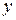
	возрастает	не существует	возрастает

Точек экстремума нет.

Вопросы для самоконтроля.

1. Какая функция называется невозрастающей?

2. Какая функция называется убывающей?

3. Сформулировать признак монотонности.

4. Что такое критические точки?

5. Какая точка называется точкой максимума?

6. Какая точка называется точкой минимума?

7. Сформулировать необходимое условие экстремума.

8. Сформулировать достаточное условие экстремума.

Задачи для самоконтроля.

Исследовать функцию на монотонность и найти точки экстремума:

а) 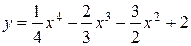, б) .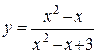

Дата добавления: 2014-01-15