Тема 4: організація і техніка проведення експертизи

Основные теоремы двойственности и их экономическое содержание

Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач. Решив одну из пары двойственных задач, можно или найти оптимальное решение другой задачи, не решая ее, или установить его отсутствие. Возможны следующие случаи:

1) обе задачи из пары двойственных задач имеют оптимальные решения;

2) одна из задач не имеет решения ввиду неограниченности целевой функции, а другая – ввиду несовместности системы ограничений.

Теорема 5.1. (Основное неравенство теории двойственности)Для всех допустимых планов x и y пары взаимно двойственных задач справедливо неравенство F (x) ≤ Z (y).

Его экономическое содержание состоит в том, что для любого допустимого плана производства x и любого допустимого вектора оценок ресурсов y, общая созданная стоимость не превосходит суммарной оценки ресурсов.

Теорема 5.2. (Достаточный признак оптимальности) Если для некоторых допустимых планов x* и y* пары двойственных задач выполняется равенство F (x*) =Z (y*), то x* и y* являются оптимальными планами соответствующих задач.

Экономический смысл критерия: план производства x и вектор оценок ресурсов y являются оптимальными, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.

Теорема 5.3. (Существование оптимальных планов пары двойственных задач) Для существования оптимального плана каждой из пары двойственных задач необходимо и достаточно существование допустимого плана для любой из них.

Теорема 5.4. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций совпадают, то есть F (x*) =Z (y*). Если одна из двойственных задач неразрешима, вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.

Экономическое содержание теоремы:если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов, причем цена продукта полученного в результате реализации оптимального плана совпадает с суммарной оценкой ресурсов.

Связь между задачами двойственной пары глубже, чем указано в формулировке теоремы: решая симплекс-методом одну из них, автоматически получаем решение другой. Для этого достаточно воспользоваться соответствием переменных прямой и двойственной задач и оценок в последней симплекс-таблице:

.

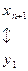
Теорема 5.5. Двойственная задача к двойственной есть прямая задача.

Теорема 5.6. Если пара двойственных задач имеет оптимальное решение, то при этом оптимальное значение переменных прямой задачи равно симплекс-множителям оптимального решения двойственной задачи, а значение переменных оптимального решения двойственной задачи равно симплекс-множителям оптимального решения прямой задачи.

МЕТА: опанувати особливості взяття зразків для митної експертизи, вивчити процеси на підготовчому, основному і заключному етапах експертизи.

Дата добавления: 2014-01-15