Введение. Дополнительный материал

Дополнительный материал

Требования к спецификации эконометрической модели

Определение эконометрики. Примеры решения эконометрических задач

Введение

Тема 1. Спецификация эконометрической модели

Журналы

1. Прикладная эконометрика

2. Квантиль.

Отдельные публикации по эконометрике появляются в журналах:

3. Экономика и математические методы,

4. Вопросы статистики,

5. Вопросы экономики

1.3. Определение слова «спецификация»

Приводим основные математические обозначения, формулы, которые будут использованы по курсу эконометрика.

Массив чисел: 10, 15, 19, 21 можно обозначить: х1, х2, х3, х4 или Хi, i = 1, 2, 3, 4

Массив чисел можно представить в разных видах:

- перечислением: х1=10, х2= 15, х3= 19, х4= 21;

- таблицами:

i	Хi

i
Хi

Сумма массива чисел - ΣХi = х1+х2+х3+х4 = 10+15+19+21= 65

i	Хi
Сумма

Среднее значение массива чисел: Хс = (ΣХi)/n = (х1+х2+х3+х4)/4 = (10+15+19+21)/4=65/4=16,25,

i	Хi
Сумма
Среднее	16,25

Вариация массива чисел: Σ(Хi-Хс)² = (х1-Хс)² + (х2-Хс)² (х3-Хс)² (х4-Хс)² = (10-16,25)²+(15-16,25)²+(19-16,25)²+(21-16,25)² = 39,06+1,56+7,56+22,56= 70,74

i	Хi	(Хi-Хс)^2
		39,06
		1,56
		7,56
		22,56
Сумма		70,74
Среднее	16,25

Дисперсия массива чисел: S² = ( Σ(Хi-Хс)²)/(n-1)= 70,74/(4-1) = 23,58,

i	Хi	(Хi-Хс)^2
		39,06
		1,56
		7,56
		22,56
Сумма		70,74
Среднее	16,25
S^2		23.58

Среднее квадратическое отклонение массива чисел: S= корень(S²) = корень (23,58) = 4,85

i	Хi	(Хi-Хс)^2
		39,06
		1,56
		7,56
		22,56
Сумма		70,74
Среднее	16,25
S^2		23.58
S		4.85

Х – матрица

Х=

Х^т – транспонированная матрица

Х^т =

Х^тХ – произведение матриц, Х^т – первая матрица, Х – вторая матрица

Х^тХ = 10*10+15*15+19+19+21*21 = 1127

Х^-1 – обратная матрица Х.

Обозначим выборочные наблюдения через

Х₁, Х₂, …, Х_n;

У₁, У₂, …, У_n

и введем их арифметические средние

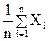`Х =,`У =,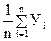

где 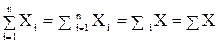= Х₁+Х₂+ …+Х_n;

X – фактор, объясняемая переменная, влияющая на следствие У;

У – следствие, зависимая переменная.

Греческими буквами обозначают параметры модели для генеральной совокупности.

Например, a₀, a₁ – параметры линейной модели У=a₀+a₁X+e для генеральной совокупности,

Где e - случайное возмущение или ошибка модели, которая состоит из ошибки уравнения и ошибки измерения.

Латинскими буквами обозначают коэффициенты уравнения регрессии для выборочной совокупности.

Например, а₀, а₁ – коэффициенты уравнения регрессии У = а₀+а₁Х+е для выборочной совокупности,

где е = У - (а₀ + а₁Х) = У - У_p -– отклонение или остаток (Гаусс называл его убытком, В эконометрической литературе принято е называть остатком), учитывающий влияние всех факторов, не включенных в модель;

У – фактические значения зависимой переменной;

У_p= а₀+а₁Х - расчетные значения У;

Х – фактор.

d - белый шум.

m – число степеней свободы.

n – объем выборки.

Т – период периодического колебания.

k – количество всех коэффициентов в модели (включая свободный коэффициент).

Например, уравнение регрессии У=а₀+а₁Х + е имеет два коэффициента: а₀ и а₁, следовательно k = 2.

t – индекс времени в моделях временных рядов.

Например, У_t = a₀+a₁X_t +e_t, t – индекс времени.

t_a1 – фактическое значение критерий Стьюдента для коэффициента а₁.

Например, t_а1 = a₁/S_a1,

где S_a1 – среднее квадратическое отклонение коэффициента а₁ от своего математического ожидания a₁, или ошибка коэффициента а₁.

t_a/2(a = 0.05, m = n - 1) или t_a/2 – двухстороннее (критическое) табличное значение критерия Стьюдента.

t_a(a = 0.05, m = n - 1) или t_a – одностороннее (критическое) табличное значение критерия Стьюдента,

где a - уровень значимости критерия или вероятность ошибки при отклонении верной нулевой гипотезы или вероятность совершить ошибку первого рода;

ошибка первого рода – неправильное отклонение нулевой гипотезы;

m = n - 1 – число степеней свободы для критерия Стьюдента.

Например, в уравнении регрессии У=а₀+а₁Х+е, У – зависимая переменная, Х – фактор.

В системах одновременных уравнений У может выступать как объясняемая переменная.

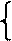У₁ = а₀+а₁Х₁+а₂У₂+ е₁,

У₂ = b₀+b₁X₂ +b₂У₁ + е₂

В первом уравнении: У₁ – зависимая переменная, Х₁ – фактор,
У₂ – объясняемая переменная.

Во втором уравнении: У₂ – зависимая переменная, Х₂ – фактор,
У₁ – объясняемая переменная.

Введем обозначения уравнения регрессии для трех переменных.

Предположим, мы имеем три связанные между собой переменные, которые обозначим через X₁, X₂, У. Переменная У может, например, отражать количество покупок некоторого товара в домашнем хозяйстве семьи, Х₁ – цена товара, Х₂ – доход семьи. Произведем выборку объемом n из генеральной совокупности, составляющая N семей. Численные значения переменных выборки мы будем записывать в таблице 0.1.

Таблица 0.1. - Исходные значения выборочной совокупности

i	X1	X2	У
	X11	X21	У1
	X12	X22	У2
i	X1i	X2i	Уi
…	…	…	…
n	X1n	X2n	Уn

Здесь Х_di обозначает величину переменной Х_d для i-го домашнего хозяйства. Гипотеза о линейной зависимости У от Х₁ и Х₂ может быть записана в виде

У_i = α₀ + α₁X_1i + α₂X_2i + e_i , i = 1, 2, …, n.

Примечание. Большинство статистических пакетов предполагает предложенную схему размещения переменных в таблице базы данных: сначала размещают столбцы факторов Х_d, последним ставят столбец зависимой переменной У.

Е – ошибка модели.

F – фактическое значение критерия Фишера.

F_кр(α = 0,05; m₁ = k - 1; m₂ = n - k) – критическое значение критерия Фишера на уровне значимости α и числе степеней свободы m₁, m₂.

S – среднее квадратическое отклонение для выборочной совокупности.

S² – дисперсия для выборочной совокупности.

s - среднее квадратическое отклонение для генеральной совокупности.

s² – дисперсия для генеральной совокупности.

М – условное обозначение математического ожидания.

Например. М(e_i) = 0 при всех i = 1, 2, …, n.

r – коэффициент корреляции.

r² – коэффициент детерминации.

R – множественный коэффициент корреляции.

R² – множественный коэффициент детерминации.

Буквы в формулах, выделенные полужирным шрифтом, означают матрицу.

Например. В формуле

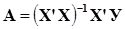А, Х, У -матрицы.

Расчетные формулы. Расчет коэффициентов регрессионного уравнения

У = а₀ + а₁Х + е

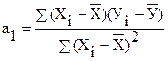
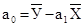
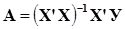где А - матрица коэффициентов модели; Х и У - матрицы соответственно факторов и зависимой переменной.

Ошибка модели:

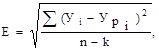
где У_рi = а₀ + а₁Х_i.

Основное вариационное уравнение

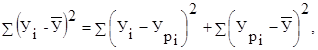
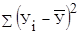
где = С_общ. – вариация общая;

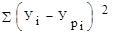
= С_ост – вариация остатков;

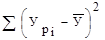
= С_рег = С_общ- С_ост – вариация регрессии.

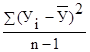
S_общ² = - дисперсия общая.

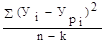
S_оcт² = - дисперсия остатков.

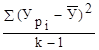
S_рег²= - дисперсия регрессии.

- коэффициент детерминации.

Множественный коэффициент детерминации:

.

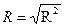Критерий Фишера:

.

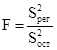
Ошибка коэффициента а₀:

.

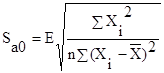
Ошибка коэффициента а₁:

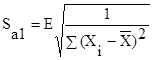
Критерий Стьюдента для коэффициента а₁:

.

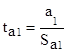
Частный коэффициент детерминации для фактора Х₁:

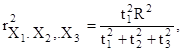
где t_i - критерий Стьюдента для фактора Х_i

Точечный прогноз:

У_пр = а₀+а₁Х_ож,

где Х_ож – ожидаемое значение Х.

95% интервальный прогноз для математического ожидания У:

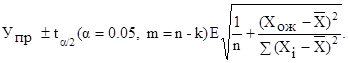
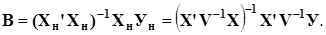Расчет коэффициентов модели методом Эйткена:

Парный коэффициент корреляции:

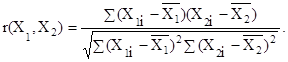
Частный коэффициент корреляции:

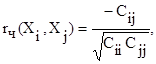
где С_ij – элементы обратной матрицы от матрицы всех парных коэффициентов корреляции.

Критическое значение коэффициента корреляции:

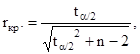
где t_a/2 = t_a/2(a = 0,05; m = n - 2).

Коэффициент автокорреляции:

.

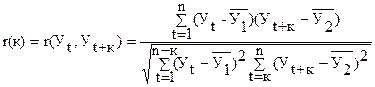Критерий Дарбина – Уотсона (Дарбина – Ватсона):

.

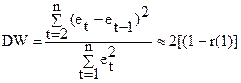Дата добавления: 2014-01-15