Требования к спецификации эконометрической модели

Конец расчетов

Оценка коэффициента ранговой корреляции Спирмена.

Значимость коэффициента ранговой корреляции Спирмена

По таблице Стьюдента находим t_табл:

t_табл (n-m-1;α/2) = (8;0.05/2) = 2.306

Поскольку Tнабл < tтабл, то принимаем гипотезу о равенстве 0 коэффициента ранговой корреляции. Другими словами, коэффициент ранговой корреляции статистически - не значим.

Интервальная оценка для коэффициента корреляции (доверительный интервал).

Доверительный интервал для коэффициента ранговой корреляции

r(-0.7353;0.7231)

Проверим гипотезу H₀: гетероскедастичность отсутсвует.

Поскольку 2.306 > 0.02, то гипотеза об отсутствии гетероскедастичности принимается.

Небходимо иучить решение задачи.

Многие понятия, которые использовались при решении задачи будут пояснены в соответствующих темах курса эконометрика

Решение было получено и оформлено с помощью сервиса:

Уравнение парной линейной регрессии

Вместе с этой задачей решают также:

Уравнение множественной регрессии

Выявление тренда методом аналитического выравнивания

Показатели вариации

Показатели динамики

1.3. Определение слова «спецификация»

Слово «спецификация» (от лат. species – род, вид, разновидность и facio – делаю) термин, обозначающий набор требований и параметров, которым удовлетворяет некоторая сущность

ГС1.2.Спецификацией эконометрической модели называется отбор факторов, включаемых в модель, и выбор математической функции для У на основании имеющейся или предполагаемой связи между переменными.

(Эконометрика: учеб./ И.И. Елисеева и др. под ред. И.И, Елисеевой. – 2-е изд., перераб. И доп. – М.: Финансы и статистика, 2005. – с. 43-47)

КС

Спецификация эконометрической модели является составной частью этапов эконометрического моделирования.

ГС1.3. Можно выделить следующие этапы эконометрического моделирования.

1- определение цели исследования;

2- определение факторов, влияющие на зависимый показатель;

3 - проверка связи между переменными;

4 - составление перечня факторов, которые могут быть включены в модель;

5 -спецификация эконометрической модели;

6 - отбор факторов, включаемых в модель множественной регрессии;

7 - оценка параметров линейных уравнений регрессии;

8 - оценка качества подбора уравнения;

9 - проверка статистической значимости модели и ее параметров;

10 - получение точечного и интервального прогноза;

11 - выводы и предложения.

КС

Все этапы эконометрического моделирования включены в темы курса.

Спецификация эконометрической модели считается произведенной, если выполнены следующие требования:

1) определены цели исследования;

2) определены факторы, влияющие на зависимый показатель;

3) проведена проверка связи между переменными;

4) имеется перечень факторов, которые могут быть включены в модель;

5) выбран вид модели, учитывающей влияние выбранных факторов;

6)- проверено условие: объем выборки должен быть в 6-7 раз больше количества факторов, включенных в модель;

7) проверено условие возможности расчета коэффициентов методом наименьших квадратов;

8) изучена возможность четкой экономической интерпретации коэффициентов модели и проведения прогнозирования.

Первое требование предполагает определение цели эконометрического исследования, соответствующей целям и задачам предприятия.

Любая организация или предприятие имеют утвержденные миссию, видение, стратегические цели и задачи на определенный период.

Цель эконометрического исследования должна соответствовать целям и задачам предприятия.

Целью эконометрического исследования может быть - проверка достижения основных плановых значений экономических показателей, таких как величина розничного товарооборота, размер валового внутреннего продукта, прибыли, издержек обращения, размера торговых запасов и т.д. с использованием эконометрических моделей.

Результатом эконометрического моделирования должно быть описание модели с результатами проверки ее достоверности, точечным и интервальным прогнозом зависимой переменной.

Второе требование предполагает определение факторов, влияющих на зависимый показатель.

Приводим классификацию основных переменных, которые используются в эконометрике.

ГС1.4. Переменная – показатель экономической системы, численные значения которого изменяются.

Фактор – причина, которая влияет на зависимую переменную.

Зависимая переменная – следствие, которое испытывает влияние со стороны факторов.

По характеру влияния на зависимую переменную факторы можно разделить на главные и второстепенные.

Основные факторы это такие факторы, без которых не будет существовать зависимая переменная. Например, для товарооборота магазина основными факторами будут: наличие товаров (предложение), наличие покупателей (спрос), наличие продавцов, площадь магазина.

Второстепенные факторы это такие факторы, которые влияют на зависимую переменную, но без которой зависимая переменная сможет существовать. Например, для товарооборота магазина второстепенными факторами будут: культура обслуживания, раскладка товара, метод обслуживания покупателей, реклама.

По признаку значений переменные разделяются на числовые и качественные.

Числовая переменная – переменная, которая имеет дискретные или непрерывные численные значения.

Качественная переменная – переменная, значения которой принадлежат к определенному классу. Например, предприятие может быть приватизированным или неприватизированным, убыточным или прибыльным, расположенным далеко или близко от источников сырья.

Фиктивная переменная – переменная, которая количественным образом описывает качественную переменную.

КС

По времени действия переменные группируются на текущие и лаговые.

Текущие переменные – переменные, которые измерены в текущий момент времени.

Пространственные переменные – переменные, которыехарактеризуют предприятия за один интервал времени

Временные переменные – переменные, которые характеризуют предприятие за несколько интервалов времени,

Пространственно-временные переменные – переменные, которые характеризуют несколько предприятий за несколько интервалов времени.

Лаговые переменные – переменные, численные значения которых измерены в предшествующие моменты времени по отношению к текущим значениям зависимой переменной.

Лаговая переменная обладает удивительным свойством – она может влиять, но не может быть зависимой, так как прошлое может влиять на будущее, но прошлое не зависит от текущего времени.

По отношению к месту нахождения в экономической системе переменные разделяются на внутренние или эндогенные и внешние или экзогенные.

Эндогенные переменные – внутренние переменные, которые принадлежат к экономической системе. При этом эндогенные переменные могут влиять на другие эндогенные переменные и могут от них зависеть. Например, если в магазине имеется очередь, то увеличение продавцов приведет к увеличению товарооборота, увеличение товарооборота приводит к увеличению продавцов. Процесс увеличения продавцов и товарооборота будет продолжаться до тех пор пока будет сохраняться очередь. Товооборот и количество продавцов являются эндогенными переменными.

Экзогенные переменные – внешние переменные, которые влияют на переменные экономической системы, но от них не зависят. Например, суточное вращение земли влияет на показатели экономической системы, но вращение земли не зависит от экономической системы.

Среднее динамическое равновесное значение переменной – значение эндогенной переменной, которое устанавливается стабильным в экономической системе

Экзогенной переменной является лаговая эндогенная переменная.

Эконометрические исследования накладывают следующие ограничения на значения переменных:

- численные значения переменной должны изменяться. Это условие обусловлено тем, что нельзя определить степень влияния переменной, значения которой не изменяются. Степень синхронности изменения переменных влияет на величину критерия их связи между собой;

- количество значений в переменной или объем выборки должен быть в 6-7 раза больше, чем количество факторов в модели;

- все переменные в модели должны иметь изменяющиеся численные значения. Если в модели используется качественная переменная, то необходимо каждому классу дать численное значение;

- численные значения переменных, по возможности, не должны содержать ошибок измерений;

- в значениях переменной не должно быть пропусков. Если какие то значений в переменной отсутствуют, то следует заполнить их средними значениями или интерполяционными значениями.

Эконометрические исследования должны учитывать следующие свойства значений переменных:

- сильно выделяющееся значение зависимой переменной (выброс) может быть результатом влияния сильно изменившегося одного влияющего фактора или является результатом однонаправленного воздействия большинства объясняющих переменных. Вероятность однонаправленного воздействия большинства объясняющих переменных очень мала. Поэтому, причиной этого явления могло послужить изменение такого синхронизирующего фактора, который одновременно повлиял на эти объясняющие переменные. В экономических исследованиях такими синхронизирующими факторами могут быть: праздники; стихийные бедствия; предвыборные компании; сезонность; события, которые вызывают ожидание перемен и другие явления, которые одновременно воздействуют на все население или только на ее часть;

- если переменные изменяются синхронно, то эти переменные связаны между собой. Если переменные изменятся хаотично или случайным образом, то эти переменные не связаны между собой.

Определение факторов, влияющих на зависимый показатель, состоит в определении главных и второстепенных факторов, оказывающих влияние на зависимый признак У.

Зависимая переменная зависит от следующих основных причин (факторов):

· -условия окружающей среды (физическая среда: температура, влажность, давление и степень загрязнения воздуха, освещенность рабочего места, уровень шума и радиации и т. д.; абстрактная среда: правовая и законодательная среда деятельности предприятия, стиль руководства, моральный климат и традиции, существующие на предприятии и т. д.);

· -оборудование;

· -материалы;

· -измерения;

· -методы;

· -люди;

· -время.

Составляется список факторов, которые могут влиять на зависимую переменную У.

В эконометрическом моделировании используется следующее правило в модель надо включать все основные факторы и несколько второстепенных.

Поэтому в список факторов должны войти все основные и некоторые второстепенные, которые являются наиболее существенными.

Третье требование предполагает проведение проверки связи между переменными.

После определения предполагаемых факторов, влияющих на зависимую переменную У, необходимо проверить эти связи на фактических данных. Для этой цели надо собрать данных для зависимой переменной У предполагаемых факторов Х.

Вычислить матрицу парных коэффициентов корреляции между У и всеми факторами для определения наличия линейной тенденции с использованием программы Ехсе1 «Корреляция».

Если зависимость У от факторов будет нелинейной, то коэффициент корреляции может быть недостоверным и эти факторы могут выйти из анализа, что приведет к ошибкам спецификации модели. Поэтому, необходимо произвести визуальный анализ графиков зависимости У от всех факторов для определения формы зависимости.

Можно определить вид зависимости У от Х по пяти функциям с помощью графических средств Ехсе1, параметры линии тренда.

После обнаружения факторов, линейно или нелинейно влияющих на У, необходимо перейти к спецификации эконометрической модели.

Все данные можно разделить на следующие виды: пространственные, временные и пространственно-временные.

Пространственные данные характеризуют деятельность нескольких предприятий за один интервал времени.

Временные данные характеризуют деятельность одного предприятия за несколько последовательных интервалов времени.

Пространственно-временные (панельные) данные характеризуют деятельность нескольких предприятий на протяжении нескольких интервалов времени.

В данной теме изучаются только пространственные данные.

При изучении временных рядов будут изучаться временные и пространственно-временные данные.

Четвертое требование предполагает выделение всех главных и некоторых второстепенных факторов, влияющих на зависимую переменную.

Пятое требование предполагает выбор вида функции может выполняться на основе экономической теории изучаемого процесса или имеющейся фактической связи между переменными.

Для выбора необходимой функции надо знать ее свойства: графики функций или какие виды тенденций она может воспроизвести, линейность коэффициентов и переменных, аддитивный или мультипликативный вид соединения коэффициентов для выбора метода расчета ее коэффициент.

Для выбора функций имеются каталоги функций с их основными графиками.

Однако, на практике используется не более 10 видов функций, которые имеются в Ехсе1.

Имеются пакеты прикладных программ, которые позволяют использовать более 2000 видов функций для воспроизведения выявленной закономерности между У и одним или несколькими факторами.

Таким образом программные средства позволяют воспроизвести любую обнаруженную закономерность между У и Х.

Если выбранная функция не соответствует экономическому процессу, то ее заменяют другой.

Шестое требование предполагает сбор данных по каждой переменной в таком количестве, чтобы превышал количества факторов в модели в 6-7 раз. Это условие выполнить трудно, особенно для временных рядов, когда количество лет анализируемого показателя очень ограниченно или имеется ограниченное количество предприятий. Очень часто в многофакторных моделях количество факторов может превышать объем выборки по каждому фактору. При этом если использовать шаговый метод построения модели, то в результате в полученной модели третье условие может быть выполнено.

Седьмое требование предполагает проверку возможности проведения расчетов с помощью МНК.

Расчеты коэффициентов модели МНК можно произвести, если:

- модель является линейной относительно коэффициентов и переменных,

- коэффициенты модели соединены аддитивно,

- количество факторов в модели меньше объема выборки.

Дадим более подробное пояснение к этим условиям.

Общий вид множественной регрессионной модели для выборочной совокупности имеет следующую структуру:

Уi= f(Х1i, Х2i, Х3i,...) + еi = Урi + ei,

где Уi- случайная зависимая переменная,

Урi - расчетные значения зависимой переменной,

f(Х1i, X2i, X3i,...) - математическая функция отражает детерминированную составляющую Уi, которая диктуется законодательной, правовой средой общества в сочетании с потребностями членов общества, закономерностями существующими между экономическими показателями,

Х1i, X2i, X3i, … –факторы, оказывающие влияние на Уi,

еi = Уi – Уpi - случайная составляющая (остатки, возмущения) Уi, которая содержит ошибки спецификации, ошибки выборки и ошибки измерения.

i - порядковый номер измерения i = 1,..., n,

n - oбъем выборки, при этом объем выборки должен быть в 6-7 раз больше количества факторов, включенных в модель.

В зависимости от количества факторов в модели различают однофакторные (парные, простые) и многофакторные модели.

Приводим общий вид линейной однофакторной (парной, простой) регрессионной модели для выборочной совокупности

Уi = а0 + а1*Хi + еi = Урi + еi,

где а0 – свободный коэффициент, равный Ур при Х = 0,

а1 – коэффициент пропорциональности зависимости Ур от Х, численно равный приросту Ур при изменении Х на 1;

е – остатки модели, которые содержат ошибки спецификации, ошибки выборки и ошибки измерения.

Приводим общий вид линейной трехфакторной регрессионной модели для выборочной совокупности

Уi= a0 + a1*Х1i + a2*Х2i + a3*Х3i + ei,

где Х1, Х2, Х3- факторы, независимые переменные, оказывающие влияние на У.

Приводим классификацию регрессионных моделей по признаку линейности коэффициентов, переменных, виду соединения коэффициентов.

Коэффициенты регрессии являются линейными, если выполняется два условия:

а) коэффициенты находятся в первой степени,

б) коэффициенты не являются степенью по отношению к другим коэффициентам или переменной.

Переменные являются линейными, если они находятся в первой степени.

Коэффициенты регрессии могут соединяться между собой аддитивно (сложением) или мультипликативно (умножением).

Линейность уравнения регрессии определяют по коэффициентам и по переменным.

Например,

Линейными уравнениями по коэффициентам и по переменным, коэффициенты соединены аддитивно являются следующие регрессии:

У = а0 + а1*Х1 + е – линейное уравнение регрессии, так как коэффициенты а0, а1и переменные У, Х имеют степень 1, коэффициенты соединены аддитивно (сложением).

Уt= a0 + a1*Х1t + a2*Х1(t-1) + a3*Х1(t-2) + et - модель распределенного лага - зависимость последующих значений зависимой переменной от предыдущих значений объясняемой переменной.

Уt= a0 + a1*Хt + a2*e(t-1) - модель, учитывающая автокорреляцию остатков - зависимость последующих значений остатков модели от своих же предыдущих значений.

Уt= a0 + a1*Хt + a2*У(t-1) + a3*У(t-2)+ et - авторегрессионная модель, учитывающая влияние на У от их же предыдущих значений.

Модель считается линейной по коэффициентам, нелинейной по переменным и аддитивным остаткам, если выполняются следующие условия:

- коэффициенты имеют первую степень

- переменные имеют степень, отличную от 1;

- коэффициенты связаны аддитивно;

- остатки включены в модель аддитивно.

Пример линейной модели по коэффициентам, нелинейной по переменным и аддитивным остаткам:

Уi= а0 + а1*Хi + а2*Хi² + еi – параболическая модель;

Уi= а0 + а1/Хi + еi – гиперболическая модель;

Уi= а0 + а1*Ln(Хi) + еi – логарифмическая модель

Уt= a0 + а1*t + a2*Sin(2*3.14*t/T) + а3*Cos(2*3.14*t/T) + et – периодическая модель,

где t - время (1, 2,..., n),

Т - период колебания.

(Уi/|еi|)= a0/|еi| + a1*(Хi/|ei|) + vi - модель, устраняющая гетероскедастичность остатков (взвешенная регрессия, обобщенный метод наименьших квадратов).

Можно составлять комбинированную функцию, которая состоит из нескольких функций с различными преобразованиями переменных: Х², X^1/2, 1/X, lnX, Sin(X), например:

Уi= а0 + а1*Ln(Хi) + а2* Х² + а3*1/X + еi – комбинированная модель является линейной по коэффициентам и нелинейная по переменным с аддитивными остатками.

В нелинейной регрессии 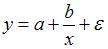параметры имеют степень 1, а объясняющая переменная х имеет степень, отличную от 1.

Коэффициенты уравнения регрессии можно рассчитать методом наименьших квадратов, если коэффициенты являются линейными и соединены аддитивно (сложением).

Если к регрессионному уравнению не применим метод наименьших квадратов, то есть три пути:

- преобразовать его к линейному аддитивному виду;

- предложить специально разработанные формулы расчетов коэффициентов уравнения регрессии;

- использовать приближенные итеративные методы расчетов коэффициентов,

Первый путь можно реализовать с помощью логарифмирования функции и заменой преобразованной переменной.

Второй путь требует большого времени и изобретательности. Особенно много хлопот доставила логистическая функция относительно оценки предела, к которому она стремится.

Третий путь можно реализовать с помощью Ехсе1 программы «Поиск решения», в которой переменными являются определяемые коэффициенты, целевой функцией является сумма квадратов остатков с условием ее минимизации и позволяет рассчитать коэффициенты всех известных функций.

Восьмое требование спецификации модели предполагает наличие возможности четкой экономической интерпретации коэффициентов модели и возможности проведения прогнозирования.

Проблемы с экономической интерпретации коэффициентов модели возникают для преобразованных данных, которые решаются для каждой модели индивидуально.

Целью всех эконометрических моделей является получение прогноза, поэтому:

- вид математической функции для воспроизведения тенденции зависимой переменной должен быть как можно проще, по которой удобней проводить прогнозирование;

- сложная функция может воспроизводить тенденцию и часть случайной составляющей, что приводит к увеличению ошибки прогноза.

Дата добавления: 2014-01-15