Основные понятия. Візитка з її графічними ефектами (взяти багатонаповнену)

ПРИКЛАД

Візитка з її графічними ефектами (взяти багатонаповнену)

ТЕХНОЛОГІЇ тривимірної графіки для WEB: VRML

VRML (Virtual Reality Modeling Language) - мова моделювання віртуальної

реальності, вже досить давно застосовується в мережі Інтернет. Він визнаний Web

3D-консорціумом (www.web3d.org) для опису інтерактивної тривимірної графіки

і мультимедійних додатків і стандартизований. VRML-документ являє собою

звичайний текстовий файл, який містить описи тривимірних фігур і властивостей

їх поверхонь (колір, текстура матеріалу, освітлення і т.п.). Такий документ

надходить в браузер у вигляді вихідного тексту, точно так само, як і звичайний

HTML-документ. Браузер, який отримує VRML-документ, повинен вміти інтерпретувати

VRML-код.

Мова VRML був вперше запропонований Марком Песке (Mark Pesce) в 1993 році, а

його перша специфікація (VRML 1.0) була підготовлена ​​на основі формату Open

Inventor фірми SGI і вперше представлена ​​на другій конференції WWW у жовтні

1994 року. Подальший розвиток проходило вже не тільки на основі розробок

фірми SGI; до створення формату підключилися такі фірми, як Sony Research,

Mitra, і багато інших. У другому випуску формату (VRML 2.0) його інтерактивні

можливості були значно розширені. Стандарт VRML 2.0 підтримує анімацію

і звукові ефекти; для нього існує підтримка на рівні мов Java і

JavaScript. VRML 2.0 було розглянуто відкритої дискусійною групою і схвалений

багатьма компаніями, а в серпні 1996 року був прийнятий його стандарт. У грудні

1997 VRML 2.0 був офіційно замінений на VRML 97, який був вперше

представлений в лютому 1997 року в Монтереї (Каліфорнія, США). Новий стандарт

практично ідентичний специфікаціям VRML 2.0, з урахуванням редакційних поправок

і деяких незначних функціональних відмінностей. Таким чином, поточним

VRML-стандартом сьогодні є VRML 97, а в роботі знаходиться новий формат

- VRML 200x. Опис мови можна знайти на Web-сайті Web3D Consortium або по

адресою: www.vrml.org. Проте засоби і методи представлення 3D-графіки в

Інтернет продовжують постійно розвиватися і вже не обмежуються тільки

мовою VRML.

Направляющие косинусы внешней нормали к площадке, решение системы линейных однородных алгебраических уравнений (СЛОАУ), вычисление определителя третьего порядка, главные напряжения и главные площадки, инварианты напряженного состояния, экстремальные касательные напряжения, деформированное состояние в точке, главные деформации.

5.1 Главные напряжения и главные площадки

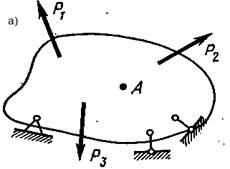
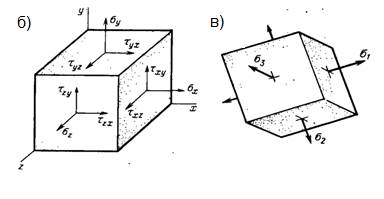
Рассмотрим некоторое тело, нагруженное системой сил, удовлетворяющей условиям равновесия (рис. 5.1 а). Тремя парами параллельных плоскостей выделим в окрестности точки А элементарный параллелепипед (рис. 5.1 б).

Рис. 5.1 Объемное напряженное состояние (а). Главные площадки (б)

Напряжения, действующие на гранях элементарного параллелепипеда в общем случае объемного напряженного состояния (рис. 5.1 б), сведем в матрицу (тензор напряжений)

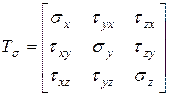
(5.1)

Если записать уравнения равновесия параллелепипеда: сумма моментов всех сил относительно осей x,y,z, то получим численные равенства закона парности касательных напряжений:

, ,

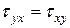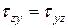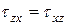
(5.2)

В двух взаимно перпендикулярных площадках составляющие касательных напряжений, перпендикулярные общему ребру, равны друг другу и направлены обе либо к общему ребру, либо от ребра. Поэтому матрица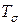симметрична. Меняя ориентировку параллелепипеда (рис. 5.1 в), можно найти такое его положение, когда на всех гранях касательные напряжения будут равны нулю. Такие площадки и действующие на них нормальные напряжения называются главными напряжениями и главными площа дками.

Рассмотрим способ их определения. Предположим, что нам известен наклон какой-либо главной площадки, определяемой нормалью γ (рис.5.2 а). Направляющие косинусы нормали:

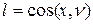
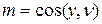
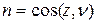
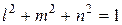
(5.3)

Сечением, параллельным этой площадке, выделим из исходного параллелепипеда тетраэдр (рис 5.2 б).

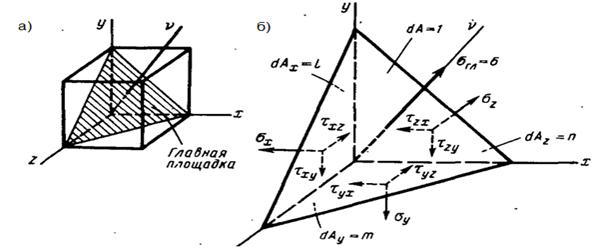
Рис. 5.2 Наклонная площадка (а) и равновесие тетраэдра, выделенного главной площадкой (б)

Примем площадь наклонной грани тетраэдра dA=1, тогда площади других граней будут равны:

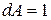
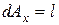
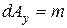
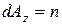
(5.4)

Напряжение, действующее на главной площадке, обозначим σ_гл=σ. Составим условия равновесия тетраэдра в виде суммы проекций действующих на него сил на ось x:

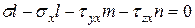
(5.5)

Аналогичные уравнения будут для осей y,z. Все вместе запишем эти уравнения в виде системы линейных однородных алгебраических уравнений (СЛОАУ) относительно неизвестных направляющих косинусов :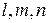

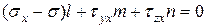
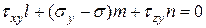
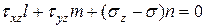
(5.6)

Решение СЛОАУ 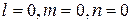нам не подходит, т.к. должно выполняться условие (5.3): .

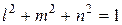Поэтому найдем решение (5.6) отличное от нуля. Для этого, потребуем чтобы определитель системы равнялся нулю, т.е.

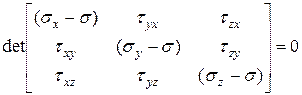
(5.7)

Раскрываем определитель (5.7) получаем:

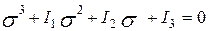
(5.8)

Из симметрии матрицы определителя (5.6) следует, что все три корня уравнения (5.8) будут действительные числа:

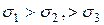
(5.9)

Коэффициенты уравнения (5.8) с учетом закона парности касательных напряжений (5.2) вычисляются по формулам:

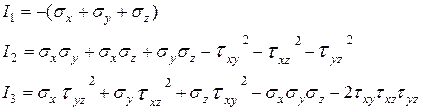
(5.10)

Коэффициенты (5.10) не зависят от выбора осей координат, так как при любых исходных площадках уравнение (5.8) должно давать одни и те же корни: 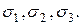Поэтому величины 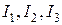называются первым, вторым и третьим инвариантами напряженного состояния (тензора напряжений).

Для определения 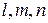, соответствующих одному из трех главных напряжений, значение этого напряжения надо подставить в уравнение (5.6) вместо σ. Совместное решение (5.6) и (5.3) даст искомые направляющие косинусы.

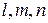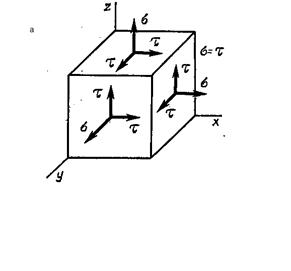
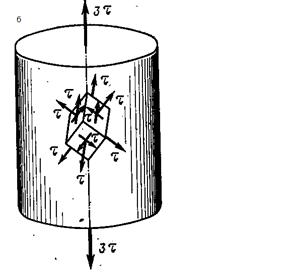
Пример 5.1 Предположим, что рассматривая напряженное состояние в точке, мы выделили в ее окрестности элементарный параллелепипед и на его гранях обнаружили систему нормальных и касательных напряжений, обладающих тем свойством, что все компоненты оказались равными друг другу τ (рис. 5.3 а). Определим главные напряжения и установим, что же это за напряженное состояние.

Рис. 5.3 Напряжения на гранях параллелепипеда (а). Выделение элементарного параллелепипеда исходного состояния (б)

Вычислим инварианты по формулам(5.10), уравнение (5.8) примет вид, корни которого равны:

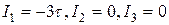
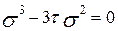
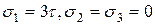
Таким образом, на рис 5.3 а представлено одноосное напряженное состояние с напряжением (Рис 5.3 б). На рис 5.3 б показана тройка взаимно перпендикулярных секущих площадок имеющих равный наклон к оси растянутого стержня.

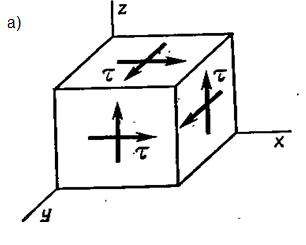
Пример 5.2 Предположим, что рассматривая напряженное состояние в точке, мы выделили в ее окрестности элементарный параллелепипед и на его гранях обнаружили систему только равных касательных напряжений τ.

Рис. 5.4 Напряженное состояние в точке (а), главные площадки исходного состояния (б)

Вычислим инварианты по формулам(5.10), уравнение (5.8) примет вид, корни которого равны:

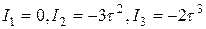
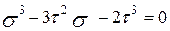
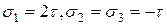
Следовательно, рассматриваемое состояние является трехосным (рис. 5.4 б).

Если площадки элементарного параллелепипеда, выделенного в окрестности точки, являются главными, то для инвариантов напряженного состояния имеем следующие формулы:

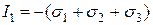
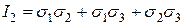
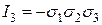
(5.11)

5.2 Площадки экстремальных касательных напряжений.

Максимальное касательное напряжение для данной точки равно полуразности максимального и минимального главных напряжений и действует на площадке, наклоненной к ним под углом 45⁰ ().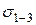

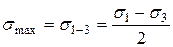
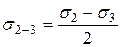
(5.12)

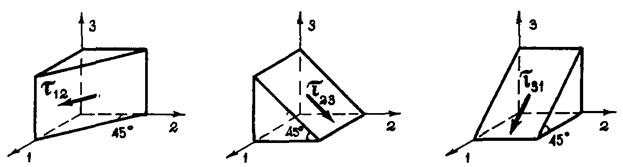
Рис 5.5. Площадки экстремальных касательных напряжений (оси 1,2,3 параллельны главным напряжениям )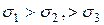

5.3 Деформированное состояние в точке

Рассмотрим особенности деформирования материала в окрестности точки М деформированного тела (рис.5.6). Выделим элемент dx_*dy_*dz в этой точке

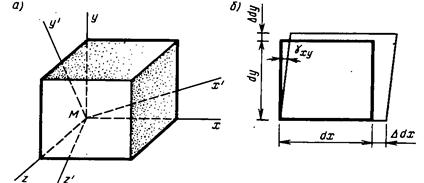
Рис. 5.6 Совокупность деформаций для всевозможных осей, проведенных через точку М, представляет деформированное состояние в точке (а); деформации элемента в плоскости x-y (б)

Деформации элемента в трех ортогональных плоскостях представим в виде тензора деформаций (см. 1.4):

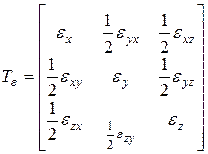
(5.13)

Если мысленно вращать вокруг точки М оси x, y, z, переводя их во всевозможные положения 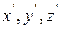,то деформации (5.13) будут непрерывно изменяться (рис. 5.6 а).

Совокупность относительных удлинений и углов сдвига для всевозможных направлений осей, проведенных через данную точку, называется деформированным состоянием в точке.

Деформации 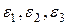в направлениях, для которых отсутствуют углы сдвига, называются главными деформациями в точке и определяются по формулам:

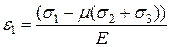
(5.14)

Дата добавления: 2014-01-15