
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логические операции. Для изучения логических операций введем следующую систему обозначений:
|
|
|
|
Для изучения логических операций введем следующую систему обозначений:
· простые высказывания будем обозначать буквами a, b, c, …, x, y,z;
· значения истинности будем обозначать 1 – истинно, 0 – ложно.
Действия логических операций будем представлять в виде таблиц истинности.
1. Отрицание или инверсия (Ø – НЕ)
Пример.
а: 7 делится на 5 без остатка.
Øа: Неверно, что 7 делится на 5 без остатка.
| а | Øа |
Эта таблица и принимается в качестве определения операции отрицания.
2. Конъюнкция (Ù,&, ·, логическое И)
Действие операции определяется следующим образом: сложное высказывание а&b истинно только в том случае, когда оба высказывания (а и b) имеют значение истинно.
| а | b | а&b |
Примеры.
а. 6 делится на 3 без остатка (1);
b. 10 больше 5 (1);
с. 7 делится на 3 без остатка (0);
d. 3 больше 7 (0);
a&b=1
a&c=0
c&d=0
3. Дизъюнкция (Ú,+,логическое ИЛИ)
Действие операции определяется следующим образом: сложное высказывание аÚв ложно только в том случае, когда оба высказывания (а и в) ложны.
| a | b | aÚb |
Примеры.
аÚb=1
aÚc=1
cÚd=0
4. Импликация (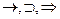 ) “если а, то b”
) “если а, то b”
Действие операции определяется следующим образом: сложное высказывание а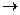 b ложно только в том случае, когда а истинно, а b – ложно.
b ложно только в том случае, когда а истинно, а b – ложно.
| a | b | a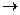 b b
|
А называется антецедентом, а b – консеквентом.
5. Эквивалентность (~ )
)
Действие операции определяется следующим образом: сложное высказывание а~b истинно, если а истинно и b истинно, или если а ложно и b ложно.
| a | b | a~b |
Эквивалентность примерно соответствует употреблению выражения «тогда и только тогда».
6. сумма по модулю два 
| a | b | a b b
|
7. Штрих Шеффера (ê, обратная конъюнкция И – НЕ)
| a | b | a ê b |
8. Стрелка Пирса ( , обратная дизъюнкция ИЛИ – НЕ)
, обратная дизъюнкция ИЛИ – НЕ)
| a | b | a b b
|
Используя эти логические операции можно строить сколь угодно сложные высказывания.
Приоритет выполнения операций:
⌐ & Ú 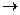 ~
~  ê
ê
Пример: Сложное высказывание: «Если вы не пропускаете занятия и успешно занимаетесь, то Вы сдадите экзамен хорошо» можно записать следующим образом. Обозначим:
П – пропускаете занятия;
Y – успешно занимаетесь;
Х – сдадите экзамен хорошо,
тогда все высказывание запишется:

Значение истинности всего выражения будет зависеть от истинности переменных обозначающих простые высказывания.
Пример.

Пусть a=1, b=0, c=0, d=1.

Символы ⌐ & Ú  ~
~  ê
ê называются пропозициональными связками, a, b, c, … и т. д. - пропозициональными переменными. Выражение, построенное из пропозициональных переменных с помощью пропозициональных связок, называется пропозициональной формой или формулой.
называются пропозициональными связками, a, b, c, … и т. д. - пропозициональными переменными. Выражение, построенное из пропозициональных переменных с помощью пропозициональных связок, называется пропозициональной формой или формулой.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 430; Нарушение авторских прав?; Мы поможем в написании вашей работы!