
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Машины Тьюринга. Конкретизация понятия алгоритма
|
|
|
|
Конкретизация понятия алгоритма
Свойства алгоритмов
Интуитивное понятие алгоритма
Тема 5. Теория алгоритмов
Для решения ряда однотипных задач можно использовать чисто механические вычислительные процессы. С их помощью искомые величины вычисляются последовательно из данных величин по определенным правилам. Описание таких процессов принято называть алгоритмами.
Алгоритм – это строгое предписание, определяющее вычислительный процесс как последовательность шагов, которая приводит от изменяемых начальных данных к конечному результату. Это фундаментальное и неопределяемое понятие.
2. Массовость: алгоритм должен решать не одну конкретную задачу, а целый класс подобных задач.
3. Элементарность шагов: алгоритм разбивается на этапы, каждый из которых должен быть простым и локальным.
4. Детерминированность: после выполнения очередного этапа однозначно определено, что делать дальше.
5. Результативность: алгоритм должен приводить к решению задачи за конечное число шагов.
Примеры алгоритмов:
1. Нахождение наибольшего общего делителя.
2. Вычисление ранга целочисленной матрицы.
3. Построение ДНФ и КНФ в логике высказываний.
Интуитивное понятие алгоритма позволяет определить является ли данный процесс алгоритмом. Но существуют и алгоритмически неразрешимые задачи, т.е. задачи для которых построить алгоритм в принципе невозможно.
Теория алгоритмов занимается проблемой алгоритмической разрешимости, т. е. определением того, возможно ли вообще построить алгоритм для задач данного типа.
Но для того, чтобы доказать, что алгоритм не существует, надо точно знать, что такое алгоритм.
Начиная с 30-х годов XX века, было предложено несколько уточнений понятия алгоритма. К ним относятся:
· Рекурсивные функции.
· Машина Тьюринга.
· Нормальные алгорифмы Маркова.
Задачу алгоритмической разрешимости можно сформулировать следующим образом: задача алгоритмически разрешима, если для нее можно построить рекурсивную функцию (машину Тьюринга, λ – нотацию, алгорифм Маркова).
Машина Тьюринга (МТ) – это математическая модель идеализированного вычисляемого устройства. Для построения МТ надо задать:
1. Конечный алфавит 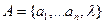 , где
, где  - пустой символ.
- пустой символ.
2. Конечное множество внутренних состояний 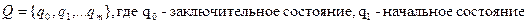 .
.
МТ представляет собой
· Бесконечную ленту, разделенную на ячейки. В каждый момент времени в ячейке записана буква 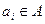 . В процессе работы в ячейку может быть записан другой символ
. В процессе работы в ячейку может быть записан другой символ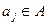
· По ячейкам передвигается управляющее устройство (УУ). В каждый момент времени оно находится напротив какой-то ячейки и имеет некоторое состояние 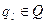 .
.
Машина действует дискретно, т. е. в определенные моменты времени.

Если в какой-то момент времени УУ воспринимает ячейку, содержащую символ  и МТ находится в состоянии
и МТ находится в состоянии 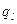 , то МТ может совершить следующие действия:
, то МТ может совершить следующие действия:
1. Стереть символ  и записать на его место символ
и записать на его место символ 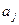 .
.
2. Переместиться в ячейку слева (Л).
3. Переместиться в ячейку справа (П).
4. Остаться на месте (С).
Эти действия называются программой.
Таким образом, М=<A,Q, П>.
Программу МТ можно представить в виде последовательности команд вида: 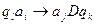 ,
,
где D={Л, П, С}. (Л- переход влево, П – переход вправо, С – остаться на месте).
Программу также можно представить в виде таблицы:
| q1 | q2 | …. | qn | |
| a1 | ||||
| a2 | ||||
| …. | 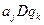
| |||
| am |
Пример. МТ добавляет к слову единицу.

| 
| 
| 
|
Программа:
 (Если в воспринимаемой ячейке символ
(Если в воспринимаемой ячейке символ  , и МТ находится в состоянии q1, то состояние не меняется, символ не меняется, УУ сдвигается вправо).
, и МТ находится в состоянии q1, то состояние не меняется, символ не меняется, УУ сдвигается вправо).
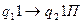 (Если в воспринимаемой ячейке символ 1, и МТ находится в состоянии q1, то это значит, что УУ находится на начале слова, состояние меняется на q2, символ не меняется, УУ сдвигается вправо).
(Если в воспринимаемой ячейке символ 1, и МТ находится в состоянии q1, то это значит, что УУ находится на начале слова, состояние меняется на q2, символ не меняется, УУ сдвигается вправо).
 (Если в воспринимаемой ячейке символ 1, и МТ находится в состоянии q2, то это значит, что УУ передвигается по слову, состояние не меняется, символ не меняется, УУ сдвигается вправо).
(Если в воспринимаемой ячейке символ 1, и МТ находится в состоянии q2, то это значит, что УУ передвигается по слову, состояние не меняется, символ не меняется, УУ сдвигается вправо).
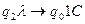 (Если в воспринимаемой ячейке символ
(Если в воспринимаемой ячейке символ  , и МТ находится в состоянии q2, то это значит, что УУ дошло до конца слова, состояние меняется на заключительное, символ меняется на 1, УУ останавливается).
, и МТ находится в состоянии q2, то это значит, что УУ дошло до конца слова, состояние меняется на заключительное, символ меняется на 1, УУ останавливается).
В виде таблицы эту программу можно записать следующим образом:
| q1 | q2 | |

| 
| 
|
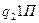
| 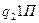
|
Конфигурация МТ (машинное слово) – это слово вида 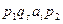 , где
, где
p1 – слово в алфавите МТ (может быть пустое),
qs – внутреннее состояние М,
ai – воспринимаемый символ,
p2 – слово в алфавите МТ.
МТ переводит конфигурацию 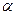 в конфигурацию
в конфигурацию  (
(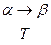 ), если
), если 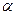 имеет вид
имеет вид 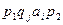 ,
,  имеет вид
имеет вид 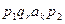 ,
, 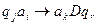 - одна из команд МТ.
- одна из команд МТ.
Для рассмотренного выше примера:
1. Команда  переводит МТ из конфигурации
переводит МТ из конфигурации  в конфигурацию
в конфигурацию 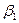

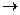

2. Команда 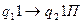 переводит МТ из конфигурации
переводит МТ из конфигурации  в конфигурацию
в конфигурацию 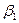
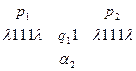
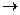
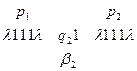
и т. д.
МТ останавливается при конфигурации 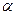 , если не существует такой конфигурации
, если не существует такой конфигурации  , что
, что 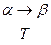 (т. е.
(т. е. 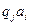 входит в
входит в 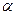 , а среди команд МТ нет такой, которая бы начиналась с
, а среди команд МТ нет такой, которая бы начиналась с 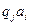 ).
).
Тезис Тьюринга: Любой интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 506; Нарушение авторских прав?; Мы поможем в написании вашей работы!