Элементы высшей алгебры

Основные понятия теории множеств.

Определение. Множеством М называется объединение в единое целое определенных различимых объектов а, которые называются элементами множества.

а Î М

Множество можно описать, указав какое – нибудь свойство, присущее всем элементам этого множества.

Множество, не содержащее элементов, называется пустым и обзначается Æ.

Определение. Если все элементы множества А являются также элементами множества В, то говорят, что множество А включается (содержится) в множестве В.

А

В

А Ì В

Определение. Если А Í В, то множество А называется подмножеством множества В, а если при этом А ¹ В, то множество А называется собственным подмножеством множества В и обозначается А Ì В.

Для трех множеств А, В, С справедливы следующие соотношения.

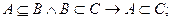
Связь между включением и равенством множеств устанавливается следующим соотношением:

Здесь знак Ù обозначает конъюнкцию (логическое “и”).

Операции над множествами.

Определение. Объединением множеств А и В называется множество С, элементы которого принадлежат хотя бы одномк из множеств А и В.

Обозначается С = А È В.

А

В

Геометрическое изображение множеств в виде области на плоскости называется диаграммой Эйлера – Венна.

Определение. Пересечением множеств А и В называется множество С, элементы которого принадлежат каждому из множеств А и В.

Обозначение С = А Ç В.

А С В

Для множеств А, В и С справедливы следующие свойства:

А Ç А = А È А = А; A È B = B È A; A Ç B = B Ç A;

(A Ç B) Ç C = A Ç (B Ç C); (A È B) È C = A È (B È C);

A È (B Ç C) = (A È B) Ç (A È C); A Ç (B È C) = (A Ç B) È (A Ç C);

A È (A Ç B) = A; A Ç (A È B) = A;

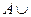Æ = А; A Ç Æ = Æ;

Определение. Разностью множеств А и В называется множество, состоящее из элементов множества А, не принадлежащих множеству В.

Обозначается С = А В.

А В

Определение. Симметрической разностью множеств А и В называется множество С, элементы которого принадлежат в точности одному из множеств А или В.

Обозначается А D В.

А D В = (A B) È (B A)

A B

Определение. С_Е называется дополнением множества А относительно множества Е, если А Í Е и C_Е = Е A.

A E

Для множеств А, В и С справедливы следующие соотношения:

A B Í A; A A = Æ; A (A B) = A Ç B;

A D B = B D A; A D B = (A È B) (A Ç B);

A (B È C) = (A B) Ç (A C); A (B Ç C) = (A B) È (A C);

(A È B) C = (A C) È (B C); (A Ç B) C = (A C) Ç (B C);

A (B C) = (A B) È (A Ç C); (A B) C = A (B È C);

(A D B) D C = A D (B D C); A Ç (B D C) = (A Ç B) D (A Ç C);

A È C_EA = E; A Ç C_EA = Æ; C_EE = Æ; C_EÆ = E; C_EC_EA = A;

C_E(A È B) = C_EA Ç C_EB; C_E(A Ç B) = C_EA È C_EB;

Пример. Исходя из определения равенства множеств и операций над множествами, доказать тождество и проверить его с помощью диаграммы Эйлера - Вейна.

Из записанных выше соотношений видно, что

Æ= A В

Что и требовалось доказать.

Для иллюстрации полученного результата построим диаграммы Эйлера – Вейна

А В А В

AÇB

Пример. Исходя из определения равенства множеств и операций над множествами, доказать тождество.

A (B È C) = (A B) Ç (A C)

Если некоторый элемент х Î А (В È С), то это означает, что этот элемент принадлежит множеству А, но не принадлежит множествам В и С.

Множество А В представляет собой множество элементов множества А, не принадлежащих множеству В.

Множество А С предсталяет собой множество элементов множества А, не принадлежащих множеству С.

Множество (A B) Ç (A C) представляет собой множество элементов, которые принадлежат множеству А, но не принадлежат ни множеству В, ни множеству С.

Таким образом, тождество можно считать доказанным.

Алгебраические структуры.

Определение. Полем называется коммутативное кольцо, в котором для любого ненулевого элемента a¹ 0 и любого элемента b существует единственный элемент х такой, что ax = b.

Дата добавления: 2014-01-15