Елементи теорії графів

При викладі попереднього матеріалу вже були використані моделі у вигляді графів. Поряд з теоретико-множинним описом моделей систем подання у вигляді графів є одним з найпоширеніших.

Граф Г – геометрична фігура, побудована на множині вершин V = {v₁, v₂, … v_m} і ребер R = {r₁, r₂, … r_n}:

Г = (V, R). (3.1)

Якщо ребра орієнтовані, то їх називають дугами, а граф - орієнтованим (орграфом). При цьому вершини називаються вузлами.

а) б)

Рис. 3.1

Приклади використання графів для моделювання:

1. Неорієнтовані графи описують (моделюють) дороги між населеними пунктами А, B, C і D (див. мал. 3.1, а).

2. Орграф описує односпрямовані канали передачі інформації (див. мал. 3.1, б).

Дуга r_i, пов'язана зі злом v_j, називається інцидентною цьому вузлу, причому, якщо заходить – позитивно інцидентна, якщо виходить – негативно інцидентна.

Два вузли v_k і v_i суміжні, якщо їм інцидентна одна дуга. Аналогічно, дві дуги суміжні, якщо вони інцидентні одному вузлу, причому, якщо одна виходить, а інша заходить - послідовно суміжні, у противному випадку - паралельно суміжні.

Дуга, що виходить із вузла й у неї ж заходить, називається петлею.

Вузол, з якого дуги тільки виходять, називається джерелом, а в який тільки заходять – стоком. Вузли стік і джерело - висячі вузли.

Дві системи S₁ і S₂ із заданими на них відносинами R₁ і R₂ ізоморфні, якщо:

1) їхні структурні елементи попарно взаємно однозначно відповідають один одному;

2) підмножина елементів А₁ системи S₁ зв'язано відношенням R₁, тоді відповідна підмножина (див. п. 1) А₂ системи S₂ зв'язано відношенням R₂.

Існує гомоморфізм – спрощена модель вихідної системи, тобто не виконуються які-небудь із вищевказаних умов.

Зв'язку в системі можна зображувати подвійно:

1) елементи – це вершини, а зв'язку – дуги (верховий граф),

2) елементи – дуги, а зв'язку – вузли (реберний або сигнальний граф).

Структури графів можна представити як графічно, так і структурними матрицями. Відомі три види структурних матриць, ізоморфних графічної моделі графа: матриці суміжності, інцидентності (інциденції) і структури зв'язків.

Матриця суміжності – квадратна матриця А = {a_ij}, 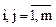, де m – число вузлів, тобто А_mxm, для якої

Число одиниць у матриці А дорівнює числу дуг n.

Ця матриця має цікаву властивість: якщо звести матрицю А в k-ю ступінь, то кожний елемент матриці А^k буде дорівнює числу шляхів з вузла v_i у вузол v_j довжиною в k дуг.

Шлях у графі - це послідовність послідовно суміжних дуг, орієнтованих в одному напрямку.

Дата добавления: 2014-01-11