Код Хеммінга

Завадостійке кодування. Двійкові та узагальнені завадостійкі коди

Теорія інформації та кодування – 2

Вступ

Л екція № 1.3 − “ Завадостійке кодування. Двійкові та узагальнені завадостійкі коди ”. В лекції будуть розглянуті наступні учбові питання:

1. Код Хеммінга. 3

2. Циклічні коди. 9

3. Узагальнені завадостійкі коди. Контрольне додавання. 12

4. Узагальнені завадостійкі коди. Лишково - матричні коди. 13

Коди Хеммінга призначені для виправлення одиночних спотворень і мають, зрозуміло, більшу надмірність, ніж коди з перевіркою на парність. У такому коді n -значне число має m інформаційних і k контрольних розрядів. При кодуванні формуються k контрольних розрядів, кожний з яких є ознакою парності для певної групи інформаційних знаків базового кодового слова.

Код Хеммінга представляє собою блочний код, який дозволяє виявити і виправити помилково переданий біт в межах переданого блоку. Звичайно код Хеммінга характеризується двома цілими числами (n, m), наприклад, (11, 7). Такий запис говорить, що при передачі 7-бітного коду використовується 4 контрольних біта (k = 11 – 7 = 4).

При цьому приймається наступна нумерація біт (знаків коду): всі біти кодової комбінації одержують номери, починаючи з 1, справа наліво (варто нагадати, що в двійковій системі числення біти нумеруються з 0 справа наліво); контрольними (перевірочними) є біти з номерами 1, 2, 4, 8 і т.д. – всі інші є інформаційними. При цьому при формуванні коду Хеммінга для наочності при кодуванні чи декодуванні інформаційні та контрольні розряди зручно представляти записаними в деякий шаблон чи таблицю. Наприклад, для семизначної двійкової послідовності 1110011:

Таблица 1
Позиция бита
Значение бита				*				*		*	*
Код номера позиції

В цій таблиці невизначені спочатку при кодуванні значення контрольних символів помічені зірочкою (*). Нагадаємо, що при використанні коду Хеммінга для передачі семирозрядних повідомлень потрібно 4 надлишкових символи
(k ³ log₂ (n + 1), k ³ 4), тобто слід використовувати код (11, 7).

Розглянемо історично перший, алгоритм із використанням k послідовних кроків (перевірок), кожна із яких забезпечує обчислення суми по модулю 2 груп символів, номери яких вибираються за певними правилами.

Щоб число в синдромі спотворень указувало номер позиції помилкового розряду, групи для перевірки вибираються за правилом:

I гр.:	:	всі непарні позиції, включаючи і позиції контрольного розряду, тобто позиції, в першому молодшому розряді яких стоїть 1.
II гр.:	:	всі позиції, номери яких в двійковому представленні мають 1 в другому розряді справа (наприклад, 2, 3, 6, 7, 10) і т.д.
III гр.	:	розряди, що мають "1" в третьому розряді справа, і т.д.

Примітка 1: У кожний з контрольних розрядів при побудові коду Хеммінга заноситься таке значення, щоб загальне число одиниць в його контрольній сумі із урахуванням контрольного було парним. Тобто, для (n, m) − коду Хеммінга перевірочні символи визначаються із перевірочних рівнянь:

де 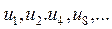− перевірочні символи.

При перевірці наявності спотворень за тими ж правилами, що розглянуті вище, розраховуються так звані елементи синдрому спотворень S _i. Але при розрахунку елементів синдрому спотворень використовуються і сформовані раніше перевірочні елементи. Тобто, елементи синдрому визначаються з виразів (синдромних рівнянь):

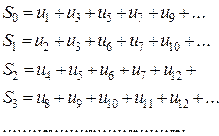
Перевірочні рівняння використовуються для побудови кодера, а синдромні − декодера коду Хеммінга.

Приклад 1. Хай передається семизначна двійкова послідовність 1110011. Як уже визначено вище, кількість перевірочних символів k = 4 та, відповідно, загальна довжина коду n = 11 (див. табл. 1). Тоді позиції контрольних біт та позиції, що перевіряються, у відповідних перевірках надано в (табл. 2).

Таблица 1
Позиция бита
Значение бита				*				*		*	*
Код номера позиції

Таблиця 2. Формування контрольних груп

Номер перевірки	Позиція контрольного біту	Позиції, що перевіряються
		1, 3, 5, 7, 9, 11
		2, 3, 6, 7, 10, 11
		4, 5, 6, 7
		8, 9, 10, 11

Отже, значення контрольних біт визначимо із системи перевірочних рівнянь:

Отже контрольна сума та значення відповідних контрольних символів дорівнюють 1110, а таблиця 1 набуде вигляду (табл. 3):

Таблица 3
Позиція біт
Значення біт

Нехай при передаванні спотворень символів не відбулося. Тоді система синдромних рівнянь набуде вигляду:

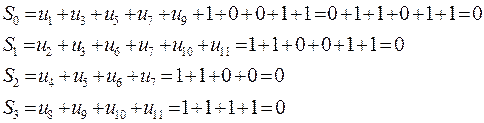
Отже контрольна сума та значення відповідних символів синдрому дорівнюють 0000, що свідчить про відсутність спотворень.

Тепер розглянемо два випадки спотворень в одному з біт посилки, наприклад в біті 7 (1 замість 0) і в біті 5 (0 замість 1). Здійснимо декодування для обох випадків (таблиці 4).

Таблица 4
Позиція біт
Значення біт (1)
Значення біт (2)

Тоді система синдромних рівнянь для першого випадку набуде вигляду:

Отже контрольна сума та значення відповідних символів синдрому дорівнюють 0111, що свідчить про наявність спотворення у біті із номером 7.

Система синдромних рівнянь для другого випадку набуде вигляду:

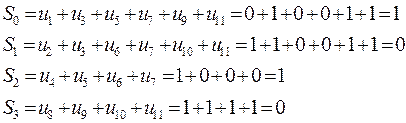
Отже контрольна сума та значення відповідних символів синдрому дорівнюють 0101, що свідчить про наявність спотворення у біті із номером 5.

Таким чином, застосування коду Хеммінга дозволило виявити як наявність так і місце спотворення.

Оскільки у двійковому коді символи можуть мати значення 0 чи 1, то у другому алгоритмі операція кодування (а в подальшому і декодування) перетворюється на додавання кодів позицій ненульових біт. Контрольне додавання здійснюється шляхом виконання операції порозрядного додавання по модулю 2 над кодами номерів ненульових бітів. У випадку послідовності за таблицею 1 – це коди біт із номерами: 11, 10, 9, 5 і 3.

Обчислимо контрольну суму (табл. 5):

Таблица 5
Номери ненульових біт	Коди їх номерів
Контр. Σ

Таким чином, приймач одержить код (табл. 6):

Таблица 6
Позиція біт
Значення біт
Значення біт за табл. 3

Порівнюючи значення біт, одержаних за цим алгоритмом та обрахованих раніше за табл. 3, упевнюємося в їх ідентичності.

Для перевірки правильності формування контрольних символів здійснимо декодування, для чого, згідно із уже визначеним алгоритмом, знову знайдемо суму кодів номерів ненульових бітів, включаючи контрольні (табл. 7), и одержимо нуль, що свідчить про відсутність спотворень:

Таблица 7
Номери ненульових біт	Коди їх номерів
Контр. Σ

Ну а тепер знову розглянемо два випадки спотворень в одному з біт посилки, наприклад в біті 7 (1 замість 0) і в біті 5 (0 замість 1). Здійснимо декодування для обох випадків (таблиця 8).

Звернемо увагу, що в обох випадках при декодуванні контрольна сума дорівнює позиції біта, переданого зі спотворенням. Тепер для його виправлення досить інвертувати біт, номер якого вказаний у контрольній сумі.

Таблица 8

Спотворено біт № 7
Σ

Спотворено біт № 5
Σ

Зрозуміло, що якщо при передачі буде спотворено більш ніж один біт, код Хеммінга при даній надмірності виявиться даремним.

Дата добавления: 2014-01-11