Частотная и фазовая модуляции

Общие сведения. При частотной модуляции вследствие изме­нения модулирующего напряжения изменяется частота несущих колебаний, а амплитуда остается неизменной. Если модуляция осуществляется гармоническим сигналом, то во время положи­тельного полупериода модулирующего напряжения частота несу­щих колебаний возрастает, а во время отрицательного полупе­риода уменьшается, т. е. Ѡ = Ѡ_н+∆Ѡcos Ωt, где ∆Ѡ—девиация частоты, пропорциональная амплитуде модулирующего сигнала.

График частотно-модулированных колебаний приведен на рис. 6.22. Из рисунка видно, что во время положительного полупериода периода модулирующего напряжения промодулированное по ча­стоте колебание опережает по фазе колебание несущей частоты, а во время отрицательного полупериода — наоборот модулирован­ное колебание отстает по фазе от несущего, т. е. частотная моду­ляция сопровождается фазовой.

Уравнение тока в антенне при частотной модуляции можно- получить, подставив в уравнение тока до модуляции значение частоты при модуляции. Известно, что уравнение для перемен­ного тока в общем виде имеет вид i=I cos ʃ Ѡdt. При постоянной частоте тока (Ѡ= const), как это было во всех предыдущих слу­чаях, уравнение для тока в антенне принимает вид i_A=I_AHcos(Ѡt+ϕ), где ϕ — начальная фаза (постоянная интегри­рования).

При частотной модуляции частота со не остается постоянной, а все время изменяется. Поэтому для вывода уравнения тока в антенне при частотной модуляции нужно под знак интеграла под­ставить значение переменной частоты. При начальной фазе ϕ = 0

уравнение тока в антенне при частотной модуляции принимает вид i_A=I_AHcos =I_AHcos 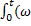_y+∆ѠcosΩt)dt=I_AHcos(Ѡ_Ht+∆Ѡ_H/ΩsinΩt).
­ Отношение девиации частоты ∆Ѡ к частоте модулирующего на­пряжения Ω, т. е. ∆Ѡ/Ω называется индексом модуляции и обо­значается буквой М.

При фазовой модуляции по закону изменения модулирующего напряжения изменяется фаза несущих колебаний, т. е. ϕ = Ѡ_нt+ -∆ϕcosΩt, где ∆ϕ — максимальное отклонение фазы, называемое индексом фазовой модуляции. Значение индекса модуляции ∆ϕ пропорционально амплитуде звукового напряжения U_Ω и не зави­сит от его частоты. Во время положительного полупериода напря­жения звуковой частоты фазомодулированного колебания опере­жает по фазе несущие колебания. Во время отрицательного по­лупериода модулированное колебание отстает от несущего. График фазомодулированного колебания приведен на рис. 6.23. Из рисун­ка видно, что с изменением фазы изменяется и частота радио­частотных колебаний, т. е. фазовая модуляция сопровождается ча­стотной.

Выражение фазомодулированного колебания можно записать так: i_A = I_AHcos(Ѡ _н t+∆ϕcosΩt ), где Ѡ _Ht — текущее значение фазы: колебаний.

При приеме фазомодулированных колебаний на радиоприем­ник с частотным детектором приемник будет реагировать на изме­нение частоты. Закон изменения частоты при фазовой модуляции определяется производной фазы

Ѡ=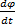==Ѡ_н+∆Ѡ+sinΩt

где ∆Ѡ = ∆ϕΩ —девиация частоты при фазовой модуляции. С уче-том этого уравнение тока в антенне принимает видi_A = I_ан cos (Ѡ_н+∆Ѡsin Ωt) t.

Сравнивая это выражение с аналогичным выражением для частотной модуляции, замечаем, что частотно-модулированное ко­лебание по форме сходно с колебанием, промодулированным по фазе, но законы изменения частоты у них разные. При модуляции косинусоидальным сигналом UcosΩt частота модулированного по фазе колебания изменяется по закону синуса, а частотно-модули­рованного— по закону косинуса. Кроме того, частотная и фазовая модуляции отличаются индексом модуляции, т. е. максимальным значением сдвига фазы. При частотной модуляции индекс моду­ляции ∆Ѡ/Ω зависит от частоты модулирующего сигнала Ω, а при фазовой — не зависит.

Различие между частотной и фазовой модуляциями наблюдает­ся при модуляции спектром частот (речью, музыкой). При частот­ной модуляции приращение частоты ∆Ѡ пропорционально только амплитуде звукового напряжения U_Ω. При фазовой модуляции приращение частоты ∆Ѡ равно произведению ∆ϕΩ и пропорци­онально не только амплитуде U_Ω, но и частоте Ω модулирующего напряжения. Поэтому при приеме фазомодулированных колебаний приемником с частотным детектором громкость звука на выходе приемника для различных частот, входящих в состав сигнала, будет различной при передаче сообщения, в котором амплитуды всех частот одинаковы. Более высокие тона передаваемого звука на выходе приемника будут звучать громче, а нижние — тише, чем перед микрофоном. Отсюда непосредственный прием фазомо­дулированных колебаний на приемник с частотным детектором не­возможен. В связи с этим фазовую модуляцию для радиосвязи не применяют. Ее используют при косвенных методах модуляции, когда сначала осуществляется фазовая модуляция, которая потом превращается в частотную.

Спектр частот при частотной и фазовой модуляциях. Анализ показывает, что модулированные по частоте или фазе колебания даже при модуляции одним тоном — сложные — и могут быть вы­ражены бесконечным рядом составляющих разных частот, ампли­туд и фаз.

При амплитудной модуляции одним тоном частоты Ω возни­кают две боковые частоты Ѡ+Ω и Ѡ — Ω. А при частотной и фа­зовой модуляциях одним тоном Я возникает бесконечно большое количество пар боковых частот Ѡ±nΩ, где n= 1, 2, 3 и т. д.

Если частотная или фазовая модуляция осуществляется слож­ным сигналом (речью, музыкой), то модулированные колебания еще более усложняются и содержат в себе ряд комбинационных боковых частот. Следовательно, при частотной и фазовой моду­ляции спектры частот бесконечно широкие.

Энергия ЧМ-колебаний распределена в широком спектре час­тот. Но условно принято считать эффективными только те коле­бания, амплитуды которых составляют не меньше 3—5 % от ам­плитуды несущей в режиме молчания.

Полоса частот между крайними эффективными боковыми ко­лебаниями называется эффективной или реальной полосой.

Амплитуды несущей и боковых частот при ЧМ и ФМ зависят от индекса модуляции. Следовательно, подбором индекса моду­ляции можно изменять ширину полосы частот. Это дает возмож­ность подобрать индекс модуляции так, что амплитуды первой па­ры боковых частот будут незначительны. В этом случае ширина спектра ЧМ-колебаний будет такой же, как и при амплитудной модуляции.

На практике различают узкополосную и широкополосную ЧМ. При узкополосной ЧМ индекс модуляции М= 1—2; спектр зву­ковых частот от 300 до 3000 Гц; реальная полоса частот от 6 до 10 кГц; спектр ЧМ колебаний состоит из одной или двух пар бо­ковых частот. Применяют узкополосную ЧМ в служебной и низо­вой радиосвязи.

При широкополосной модуляции полоса модулирующих частот от 200 до 15000 Гц; девиация частоты 75 кГц, индекс модуляции 5—8; реальная полоса излучаемых частот 150 кГц. Широкополос­ная частотная модуляция применяется при высококачественном радиовещании и для звукового сопровождения телевизионных пе­редач.

Частотная модуляция имеет ряд преимуществ перед амплитуд­ной. При частотной модуляции излучаемая передатчиком мощность­ во времени постоянна.

Это позволяет полностью использо­вать выходную мощность усилительных электронных приборов. Достоинство частотной модуляции по сравнению с амплитудной — более высокая помехоустойчивость. Амплитудные помехи при ЧМ подавляются ограничителем в приемнике.

Частотная и фазовая модуляции осуществляются в диапазоне УКВ.

Схемы частотной модуляции. Для осуществления частотной модуляции необходимо изменять частоту генератора в соответствии с передаваемым сигналом. Это можно осуществить изменени­ем частоты настройки контура задающего генератора. Для этого к контуру подключают безынерционное реактивное сопротивле­ние (индуктивность или емкость). Таким безынерционным сопро­тивлением может быть реактивная электронная лампа, транзистор или полупроводниковый диод.

В транзисторных генераторах частотную модуляцию осущест­вляют двумя способами: с помощью специальных диодов — вари­капов, параметрических диодов и др.; с помощью специальных реактивных каскадов на транзисторах.

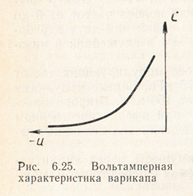Схема частотной модуляции с по­мощью варикапа приведена на рис. 6.24. В этой схеме на транзисторе VT собран автогенератор. Параллельно контуру автогенератора подключен варикап. Зарядная емкость варикапа изменяется с изменением обратного напряжения на нем так, как показано на рис. 6.25. Начальное смещение на варикап подается от отдельного источника. Напряжение звуковой частоты включается последовательно с постоянными напряжением на диоде. В результате этого напряжение на варика­пе изменяется в соответствии с изме­нением звукового напряжения, что вызывает изменение его емко­сти, а следовательно и частоты настройки контура автогенератора. По этому же закону будет изменяться и частота генерации, а сле­довательно будет осуществляться частотная модуляция.

Глава 7. ИСПЫТАНИЯ РАДИОПЕРЕДАЮЩИХ УСТРОЙСТВ

Дата добавления: 2014-01-15