
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нерегулярные потоки платежей
|
|
|
|
Обобщающие параметры потоков платежей.
Виды потоков платежей и их основные параметры
ПОТОКИ ПЛАТЕЖЕЙ
Финансовые операции часто предполагают последовательность платежей. Например, погашение задолженности в рассрочку, периодическое поступление доходов от инвестиций, выплата пенсий и т.д. Такие последовательности называют потоком платежей. Отдельный элемент этого ряда - член потока.
Виды потоков платежей. Потоки платежей могут быть регулярными и нерегулярными. В нерегулярном потоке платежей членами являются как положительные (поступления), так и отрицательные величины (выплаты), а платежи могут производиться через разные интервалы времени.
Поток платежей, все члены которого положительны, а временные интервалы между платежами одинаковы, называют рентой. Например, получение процентов по облигации, платежи по потребительскому кредиту и т.д.
Параметры ренты: член ренты - размер отдельного платежа, период ренты - временной интервал между двумя последовательными платежами, срок ренты, процентная ставка, число платежей в году, способ и частота начисления процентов.
По количеству членов различают ограниченные по срокам ренты и бесконечные, или вечные ренты.
По соотношению начала срока ренты и некоторого момента времени (например, начало действия контракта или дата его заключения), ренты делятся на немедленные и отложенные.
По моменту выплаты платежей в пределах периода. Если платежи в конце периода, то рента называется запаздывающей, если в начале периода, то - у преждающей. Иногда платежи относят к середине периодов.
Если все члены ренты одинаковы, рента называется постоянной. В дальнейшем будем рассматривать только такие ренты.
Наращенная (конечная) сумма - сумма всех членов потока платежей с начисленными на них к концу срока процентами.
Приведенная (современная) стоимость - сумма всех членов потока платежей, дисконтированных на начальный или некоторый упреждающий момент времени.
Рассмотрим общую постановку задачи определения параметров при анализе нерегулярных потоков платежей. Допустим имеется ряд платежей  , выплачиваемых спустя время
, выплачиваемых спустя время 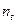 после некоторого начального момента времени, общий срок выплат
после некоторого начального момента времени, общий срок выплат  лет. Необходимо определить наращенную на конец срока сумму потока платежей. Если проценты начисляются раз в году по сложной ставке
лет. Необходимо определить наращенную на конец срока сумму потока платежей. Если проценты начисляются раз в году по сложной ставке 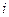 , то получим:
, то получим:


 (3.1)
(3.1)
Современная стоимость потока определяется как сумма дисконтированных платежей:
 (3.2)
(3.2)
где  - дисконтный множитель по ставке
- дисконтный множитель по ставке 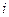 .
.
Между 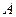 и
и 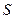 существует функциональная зависимость:
существует функциональная зависимость:

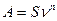 (3.3)
(3.3)
Дюрация – это средняя продолжительность поступлений. Зная современную стоимость потока платежей, для каждой выплаты  определим ее вес
определим ее вес
 .
.
Из (3.2) следует, что
 .
.
Это значит, что каждый вес 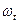 является долей современной стоимости, которую вносит выплата
является долей современной стоимости, которую вносит выплата  в момент
в момент 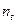 . Дюрацией называют средневзвешенную сумму
. Дюрацией называют средневзвешенную сумму
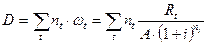 (3.4)
(3.4)
Дюрацию используют при оценке риска изменения стоимости потока платежей в связи с изменением процентной ставки. Чем больше дюрация, тем больше скачок в текущей цене потока платежей при изменении процентной ставки.
Пример 3.1.График предусматривает следующий порядок выдачи ссуды во времени (время в годах будем отсчитывать от момента первой ссуды):
0 - 5 млн.руб., 1 - 15 млн.руб., 3 - 18 млн.руб.
Необходимо определить сумму задолженности на начало четвертого года при условии, что годовая процентная ставка 20%. Схематично условия задачи приведены на рис. 3.1.
5 15 18  -? -?
Рис. 3.1 По формуле (3.1) находим
Определим современную стоимость потока на момент выплаты первой суммы. По формуле (3.2)
Определим дюрацию. Найдем веса платежей
По формуле (3.4)
|
Пример 3.2. В условиях примера 3.1 изменим график платежей: 0 - 12,53 млн.руб., 1 - 15 млн.руб., 3 - 5 млн.руб. Схематично условия задачи приведены на рис. 3.2.
12,53 15 5
  
 0 1 3
Рис. 3.2
По формуле (3.2) находим современную стоимость потока на момент выплаты первой суммы. 0 1 3
Рис. 3.2
По формуле (3.2) находим современную стоимость потока на момент выплаты первой суммы.
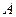 = 12,53 + 15 = 12,53 + 15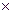 1,2-1 + 5 1,2-1 + 5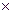 1,2-3 = 27,92 млн.руб.
Определим дюрацию. Найдем веса платежей 1,2-3 = 27,92 млн.руб.
Определим дюрацию. Найдем веса платежей
  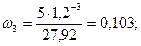 По формуле (3.4)
По формуле (3.4)
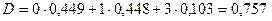 (276 дней) (276 дней)
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 845; Нарушение авторских прав?; Мы поможем в написании вашей работы!

 1,23 + 18
1,23 + 18

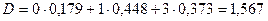 (1 год 207 дней)
(1 год 207 дней)