Лекция 10. Изоморфизм графов. Операции над графами

Содержание лекции: изоморфизм графов; подграфы и части графов; операции над графами; примеры различных видов графов.

Цели лекции: выяснить, в чём заключается понятие изоморфизма для графов и как его установить; рассмотреть некоторые операции над графами и некоторые важные виды графов.

Изоморфизм графов

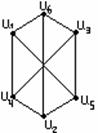
Один и тот же граф, как указывалось выше, можно изображать по - разному. Например, на рисунке 3.2.1 изображён один и тот же граф.

Рисунок 3.2.1

Вид матриц и списка рёбер зависит от нумерации вершин и рёбер. Графы, отличающиеся друг от друга только нумерацией вершин и рёбер, называют изоморфными. Приведём точное определение.

Определение. Два графа G₁=(V₁,E₁) и G₂=(V₂,E₂) изоморфны (обозначается G_1~G₂ ), если существует биекция φ:, сохраняющая смежность: e₁=(u,v)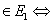 e₂=(φ(u),φ(v)).

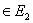Теорема. Изоморфизм графов есть отношение эквивалентности.

Действительно, изоморфизм обладает всеми свойствами отношения эквивалентности: а) рефлексивностью (G_~G); б) симметричностью (G_1~ G₂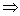 G_2~G₁); в) транзитивностью (G_1~G_2, G_2~G₃ 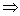G_1~G₃).

Графы рассматриваются с точностью до изоморфизма. Для того чтобы граф G₁ был изоморфен графу G₂, необходимо и достаточно существование какого-либо взаимно однозначного соответствия между вершинами графов, а также между их рёбрами. Иногда в изоморфизме графов можно убедиться по их графическому представлению. Так, например, графы и 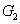на рисунке 3.2.2 изоморфны, т.к. достаточно поднять вершину 3 в графе 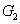до уровня вершин 2 и 4 и перевернуть 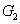, и будет видно, что и имеют одну форму.

Рисунок 3.2.2

Рассмотрим более общее правило установления изоморфизма графов: а) подсчитываем число вершин графов (если оно разное, то графы не изоморфны); б) выписываем все вершины обоих графов с их степенями (для н-графов) или с парой степеней выхода и входа (для орграфа); в) для каждой вершины первого графа ищем такую вершину второго графа, чтобы их степени или пары степеней совпадали, т.е. получим взаимно однозначное соответствие между вершинами графов (если соответствия нет, то графы не изоморфны). Практически удобно вершины одного графа располагать над вершинами другого, а соответствующие вершины соединять линией.

Подграфы и части графов

Определение.Граф G₁=(V₁,E₁) называется частью графа G=(V,E), если и E₁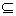E; подграфом графа G=(V,E) называется его часть G₁=(V₁,E₁), которой принадлежат все рёбра (дуги) с концами в V₁. На рисунке 3.11 изображены граф G, его подграф G₁ и его часть G_2.

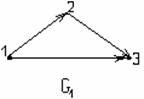
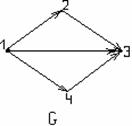
Рисунок 3.2.3

Дата добавления: 2014-01-15