Процесс моделирования

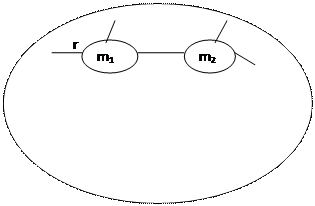
Рассмотрим простейшую модель «вход-выход»:

X Y

М = {m₁, m₂, … m_n} элементы соединены связью.

R {r₁₂ r₂₂ r… r_mn}

x {x₁, x₂, … x_n} g (x₁, x₂, … x_n)

Y { Y₁, Y₂, … Y_m} (y₁, y₂, … y_m) g (y₁, y₂, y₃, y₄)

R { m₁*m₂*…*m_n}

R {r₁ r … r_mn}

R {X C Y} g {Y₁ X₁… Y_mX_n}

пересечение параметру входа

входа и выхода; соответствует параметр выхода.

Простейшая модель «вход-выход» сформулирована как модель элементов, представляющих множество М, которые по средством имеющихся внутренних связей между элементами r определяют процесс функционирования системы.

В итоге существующих взаимосвязей определяют входы и выходы каждого элемента m в качестве совокупного входа Х и выхода У.

Совокупный вход Х представляет собой множество переменных х₁ … x_n, имеющих свои численные значения (х₁ … x_n).

Совокупный выход У представляет собой множество переменных Y₁, Y₂, … Y_m, имеющих свои координаты (y₁, y₂, … y_m).

Множество элементов М образуют отношения между входом Х и выходом У, которые обозначаются R.

Пусть множество R определяет декартовое произведение элементов системы между входом Х и выходом У, что в итоге сводится к отношению входа и выхода, задаваемое переменными входа и выхода. Т.к. R (m₁*m₂*…*m_n), тосвязи между ними можно представить в виде множества раскрывающего отношение входа и выхода.

Заменим произведение элементов на их связи:

R {X * Y} g {Y₁ * X₁ … Y_m * X_n}

Т.о. R {X * Y} (R есть отношение X на Y)

Каждому элементу входа соответствует элемент выхода (переменная - элемент).

Появляются пары элементов (x_i y_i).

Т.о. система определяется как соответствие подмножества X и Y, образуемые в результате декартового произведения входа на выход в виде множества, содержащего упорядоченные пары.

XY = {X₁Y₁ … X_iY_j}

Т.о. вход (Х), задаваемый своими числовыми значениями, физически представленных в виде каких-либо ресурсов, которые трансформируются в системе по средством внутренних свойств и взаимосвязей, которые в совокупности определяются отношением R в параметры функционирования системы Y, которая выводится во внешнею среду в множестве переменных.

Множество Y определяет результаты работы системы по средством трансформации Х через множества отношения R.

Т.о. модель системы «вход-выход» можно описать следующими отношениями Х, Y и R.

S = < Х, Y, R >

Отношение R в картеже выступает как функция изменения выходного сигнала в зависимости РТ входного и является отображением функции Х на Y.

Х g R (Y)

Когда модель R выступает в виде функции (RgF), то можно представить выход как взаимосвязь Y= F*Х; Y=f (х).

Вывод: данная модель справедлива для статических моделей, когда имеет место 1-а соответствие (1-а, степень свободы), изменяется по закону линейному и каждому входу Х соответствует единичный параметр Y.

В природе таких объектов не бывает.

Рассмотрим объект, в котором Z ≠ 1.

Система имеет состояние Z, все остальное справедливо.

R₁ R₂

X Y

Z {Z₁ Z₂ Z₃ … Z_n}

Состояние Z определяет свойство элементов в момент, зависящий от времени или от подаваемого сигнала Х.

Т.о. состояние Z как множества {Z₁ … Z_n} формируется как отражение действия внешних и внутренних факторов.

В рассматриваемый момент времени t каждая такая система имеет состояние Z, которое в момент t зависит от входа Х (состояния) и предшествующего состояния Z’ в момент времени t-1.

Т.о. можно определить отражение входа Х и предшествующего состояния Z’ на текущее состояние системы Z и определить отношение R₁, как отношение входа Х и текущего состояния Z.

(Х Z’) * R_{1 *} Z_s = (Х Z’_t-1) * R₁ * Z_t

Параметры выхода системы Y в этом случае определяется как отношение текущего состояния Z к выходу по средством отношения R₂.

Z_t * R₂ * Y

Y: надо убрать из входа Z и R₁.

Т.о. после проведения вычислений система описывается следующим картежом:

S <X Y Z_t R₁ R₂>

S_t<X Y Z_t R₁ R₂ T>

F₁ F₂

В случае динамичности системы в картеже появляется параметр времени t.

Произведение t на состояние системы дает такое множество, которое называется пространством событий, в котором наблюдаются такие единичные пары t* Z, являющиеся свершением событий функции F.

(t_j* Z_i) g F_i

В этом случае отношение R₁ определяет траекторию развития системы в пространстве, а R₂ представляет состояние системы как функцию его отношения к выходу Y.

Дата добавления: 2014-01-15