Дифференциальные уравнения

Средства описания моделей систем в функциональном пространстве

Систем управления

Математические средства описания

Линейных непрерывных систем управления

Математический аппарат анализа и синтеза

Лекция 3

Существует два основных подхода к описанию моделей систем управления:

– в функциональном пространстве;

– в пространстве состояний.

Описание в функциональном пространстве представляет собой математическое (аналитическое, функциональное) представление закона функционирования (поведения) моделируемой системы в форме математической зависимости выходного (управляемого) сигнала от входных сигналов (управления и возмущения). Это аналог модели «вход-выход».

Описание в пространстве состояний есть представление закона функционирования моделируемой системы в форме последовательности смены состояний системы и выходного сигнала под действием входных сигналов. Это аналог модели с раскрытой структурой.

Базовым средством описания динамики систем управления является аппарат дифференциальных уравнений. В зависимости от типа описываемой системы это могут быть обыкновенные дифференциальные уравнения, уравнения в частных производных, уравнения с постоянным или переменными коэффициентами и т.д. Этот аппарат достаточно развит и позволяет получать представление закона функционирования системы, из которого можно получить все необходимые характеристики системы.

Однако с ростом порядка дифференциальных уравнений, нелинейности и нестационарности, описываемых ими систем их решение становится все более затруднительным. Поэтому применяются различные способы замены дифференциальных уравнений их упрощенными эквивалентами, позволяющими облегчить процесс преобразования уравнений и получения требуемых характеристик системы.

В функциональном пространстве такими средствами для линейных систем являются преобразования Лапласа и Фурье, передаточные функции и сигнальные графы.

В пространстве состояний существуют матричные эквиваленты названных выше функциональных преобразований. Мы рассмотрим их несколько позже.

Дифференциальные уравнения (обыкновенные и в частных производных) являются одной из наиболее распространенных форм записи математической модели поведения систем управления. Дифференциальные уравнения связывают координаты вектора X состояний объектаи управляющего устройства U с входными воздействиями F на систему.

Одноконтурные системы управления (с одним входом и одним выходом) могут быть описаны одним дифференциальным уравнением некоторого вида, соответствующего виду системы. Линейные системы управления, которые мы будем рассматривать в дальнейшем, описываются обыкновенными дифференциальными уравнениями, поэтому кратко рассмотрим их. Обыкновенное линейное дифференциальное уравнение n -го порядка с постоянными коэффициентами обычно записывается так:

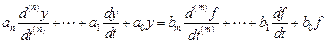, (2.1)

где y – обобщенная координата системы, определяющая, в том числе, ошибку d (t) и регулируемую величину y (t);

– f − внешняя координата, определяющая задающее g (t) и возмущающее f (t) воздействия.

Вводя оператор дифференцирования по времени и операторные полиномы

,

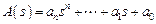
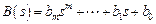можно записать дифференциальное уравнение (2.1) в более простой (алгебраической) форме:

. (2.1 а)

Обычно оно дополняется начальными условиями: y (0), y¢ (0),…, y ^{( n -1)} (0).

Дифференциальному уравнению системы управления соответствует структурная схема системы. Для составления структурной схемы по дифференциальному уравнению используется метод понижения порядка производной, который сводится к следующим этапам.

1. Положим правую часть уравнения (2.1) равной нулю иразрешимего относительно высшей производной по y.

. (2.2)

2. Предполагая левую часть полученного тождества известной в любой момент времени, с помощью цепочки интеграторов получим все производные по y (т.е. искомой функции 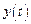)низших порядков вплоть до нулевого, как показано на рис. 2.1.

Рис 2.1. Цепочка интеграторов

3.Правая часть тождества (2.2)представляет собой сумму функций времени 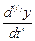, , 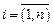взятых с постоянными коэффициентами. Просуммировав с коэффициентами, соответствующими правой части (2.2), получим старшую производную , известную по предположению в любой момент времени. Структурная реализация правой части тождества (2.2) показана на рис. 2.2.

Рис. 2.2. Структурная реализация левой части уравнения (2.2)

Теперь возвратимся снова к уравнению (2.1) и представим реализацию слагаемых, составляющих внешнее воздействие в виде, аналогичном реализации y, в результате получим его структурную схему в виде, показанном на рис. 2.3.

Рис. 2.3. Структурная реализация правой части уравнения (2.1)

4. Равенство (2.1), которое происходит из физической сущности моделируемого объекта, требует, чтобы оно (это равенство) выполнялось в каждый момент времени t. Реализовать это требование легко, достаточно замкнуть схемы, показанные на рис. 2.2 и 2.3. Результат объединения этих схем показан на рис. 2.4.

Рис. 2.4. Структурная реализация уравнения (2.2)

Установим также начальные условия, которые определяют единственность решения дифференциального уравнения.

«Запрятав» элементы структуры на рис. 2.4 внутрь системы, представим полученную реализацию в виде, показанном на рис. рис. 2.5.

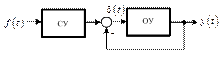
Рис. 2.5. Структурная схема системы управления

Пример 2.1. Для электрической схемы (рис. 2.6)

Рис. 2.6. Электрическая схема

составить ее математическое описание.

Решение. Выполняем первый этап разработки оператора (описание элементов). Известно, что в электрических схемах существует три типа электрических двухполюсников: резисторR, конденсаторC и катушка индуктивностиL, описываемых следующими уравнениями токов и напряжений:

,

,

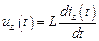
соответственно.

Выполняем второй этап разработки модели (определение

причинно-следственной структуры связей между элементами). Ак-

тивными двухполюсниками электрических схем являются источники напряжения и источники тока. Законы Кирхгофа (уравнения непрерывности токов и равновесия напряжений) для рассматриваемой цепи имеют следующий вид:

;

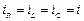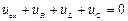; (2.4)

.

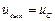Поскольку напряжения на резисторе и индуктивности могут быть выражены через напряжение на конденсаторе:

;

,

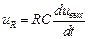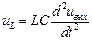то уравнения (2.4) могут теперь быть записаны в виде дифференциального уравнения второго порядка

. (2.5)

Выполняем третий этап разработки оператора системы – приведение его к некоторому стандартному виду. Положив u_вых = y, получим общий вид уравнения в виде

.

■

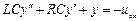Пример 2.2. Теперь рассмотрим простейший механический объект − грузик, расположенный на горизонтальной плоскости и прикрепленный пружиной к вертикальной стенке. Между горизонтальной плоскостью и грузиком находится жидкая (или не очень) смазка (рис.2.7). Получим дифференциальное уравнение его движения при растяжении и отпускании пружины.

Рис. 2.7. Механический объект

Решение. Выполняем первый этап (описание сил действующих на грузик). Грузик первоначально находился в положении равновесия (его центр масс совпадал с координатой 0 по оси Х). Под действием внешней силы F грузик переместился на величину y. При этом пружина растянулась на эту же величину. В результате на грузик стала действовать возвратная сила пружины f_пр, направленная в сторону, противоположную растяжению пружины. Кроме того, при движении грузика на него действует сила трения 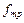, направленная против его движения, и пропорциональная скорости движения.

Выполняем второй этап. Грузик, как и любое физическое тело, подчиняется второму закону Ньютона:

(2.6)

где m − масса грузика, a − ускорение движения грузика, 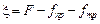− результирующая сила, действующая на грузик.

Сила, обусловленная пружиной (предполагается, что она работает в пределах упругой деформации), пропорциональна жесткости пружины и деформации, и направлена в сторону, обратную деформации, что отмечается знаком «минус»:

, (2.7, а)

где с – модуль упругости.

Сила жидкого трения, действующая на грузик, пропорциональна скорости его движения v и направлена против движения:

. (2.7, б)

Здесь k – коэффициент трения.

Подставляя в (2.6) выражения (2.7, а, б), получаем:

.

Выполняем третий этап. Если учесть, что скорость и ускорение являются соответственно первой и второй производной от перемещения:

получаем окончательный вид уравнения движения грузика:

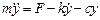
или

или

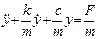. (2.8)

■

Результат – снова (как и (2.5)) обыкновенное линейное дифференциальное уравнение второго порядка. Обыкновенное дифференциальное уравнение получилось из-за того, что мы рассматривали абсолютно жесткий объект, который может быть заменен точкой с массой m, а в пружине не учитывали конечной скорости распространения волны движения. Линейным уравнение получилось из-за того, что мы рассматриваем поведение пружины в пределах диапазона упругости. При нарушении указанных условий, дифференциальное уравнение может стать нелинейным, могут появиться частные производные и т. д.

Получив решение этого уравнения, можно получить описание движения этого объекта, зависящее от начальных условий и от внешних воздействий.

Дифференциальное уравнение, решенное относительно регулируемой величины y (t) − уравнение движения. Дифференциальное уравнение (2.1, а) может быть преобразовано к виду, выражающему выходную координату через координату задания (путем исключения промежуточных координат) g (t), x ( t ), u ( t ),…, y (t). Этому преобразованию соответствует структурная схема системы, приведенная на рис. 2.8.

Рис. 2.8. Структурная схема системы для уравнения движения

Непосредственно из структурной схемы следует, что выходная переменная системы есть алгебраическая сумма реакций системы на входное воздействие 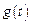и внешнее возмущение :

, (2.9)

где

R (s) = r _m s^m + r _{m −1} s^{m -1} +.. + r ₁ s + r₀

есть полином, коэффициенты которого определяют влияние задающего воздействия g (t) на регулируемую координату у (t), а

Q (s) = q _k s^k + q _{k -1} s^{k -1} +... + q ₁ s + q₀

есть полином, коэффициенты которого определяют влияние помехи f (t) на систему (моделируется обычно условным звеном). Поскольку

,

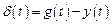то выражение (2.9) можно записать в виде

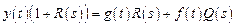
или

y (t) A (s)= g (t) R (s)− f (t) Q (s),

где

A (s) = 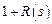= a _n sⁿ + a_{n− 1} s^{n -1} +... + a ₁ s + a₀

есть характеристический полином системы.

Дифференциальное уравнение, решенное относительно ошибки d ( t ) − уравнение ошибки. Если дифференциальное уравнение (2.1, а) преобразовать к виду, выражающему координату ошибки через координату задания, то получается уравнение ошибки замкнутой системы

A (s) d (t) = C (s) g (t) + D (s)f (t),

где

A (s) = a _n sⁿ + a _{n −1} s^{n -1} +... + a ₁ s + a₀

есть характеристический полином,

C (s) = c _n sⁿ + c _{n −1} s^{n -1} +... + c ₁ s + c₀

есть полином, коэффициенты которого определяют влияние задающего воздействия g (t) на ошибку d (t),а

D (s) = d _k s^k + d _{k −1} s^{k -1} +... + d ₁ s + d₀

есть полином, коэффициенты которого определяют влияние помехи f (t) на систему.

Такому преобразованию соответствует структурная схема, приведенная на рис 2.9.

Системы дифференциальных уравнений. Многоконтурные (многосвязные) системы управления описываются системами

Рис. 2.9. Структурная схема системы для уравнения ошибки

дифференциальных уравнений. Линейные системы управления, которые мы будем рассматривать в дальнейшем, описываются системами обыкновенных дифференциальных уравнений, поэтому кратко рассмотрим их.

Дата добавления: 2014-01-15