Понятие элементарных и типовых звеньев

Типовые звенья систем управления

Лекция 8

Ранее было показано, что передаточные функции (модели) стационарных линейных систем, описываемых обыкновенными дифференциальными уравнениями, являются дробно-рациональными функциями, т.е. отношениями полиномов с действительными коэффициентами. Такие полиномы имеют только действительные или комплексно-сопряженные корни. Из курса математики известно, что полином такого вида может быть разложен по виду корней в произведение многочленов с нулевыми (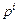), действительными () и комплексно-сопряженными () корнями. Тогда передаточная функция системы может быть представлена в виде

. (3.5)

Каждому виду сомножителей этого выражения соответствует некоторое линейное стационарное звено, передаточной функцией которого является данный сомножитель. Из (3.5) следует, что для построения модели системы управления с любой заранее заданной передаточной функцией достаточно иметь шесть типов звеньев, наименования и передаточные функции которых приведены ниже:

– идеальное дифференцирующее звено с передаточной функцией ;

– идеальное интегрирующее звено с передаточной функцией ;

– форсирующее звено первого порядка с передаточной функцией 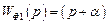, где ;

– апериодическое (инерционное) звено первого порядка с передаточной функцией 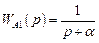, где ;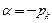

– форсирующее звено второго порядка с передаточной функцией ;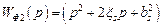

– апериодическое (инерционное) звено второго порядка с передаточной функцией ;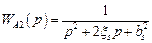

Из приведенного перечня видно, что

,

,

.

Вследствие этого логарифмические амплитудные и фазовые частотные характеристики первых трех звеньев отличаются от соответствующих характеристик последних трех звеньев только знаками. Поэтому достаточно рассмотреть первую либо последнюю тройку этих звеньев.

Однако реальные стационарные линейные системы отличаются от моделей еще двумя важными свойствами, не описываемыми передаточной функцией (3.23) – усилением и инерционностью. Моделью первого свойства служит пропорциональное звено с передаточной функцией , моделью второго - звено чистого запаздывания (идеальное запаздывающее звено) с передаточной функцией . Эти звенья должны быть включены в состав структурно полного комплекса звеньев.

Поэтому вполне допустимо классифицировать все типовые звенья систем управления следующим образом:

1. Звенья нулевого порядка (описываемые «дифференциальными уравнениями нулевого порядка», т.е. алгебраическими уравнениями) – усилительное и запаздывающее звенья.

Общее выражение передаточной характеристики звена нулевого порядка выглядит как

,

где – некоторая константа, имеющая тот или иной физический смысл (коэффициент усиления k, либо величина задержки τ). Наименования звеньев нулевого порядка и их передаточные характеристики приведены в табл. 3.1.

Таблица 3.1

Типовые звенья нулевого порядка

и их передаточные функции

Передаточная функция	Наименование звена
	Идеальное усилительное (пропорциональное)
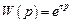
	Чистого запаздывания

2. Звенья первого порядка, описываемые общим дифференциальным уравнением первого порядка следующего вида:

.

Общее выражение передаточной характеристики звена, описываемого этим дифференциальным уравнением, имеет вид

,

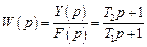где 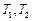– постоянные времени.

Наименования звеньев первого порядка и вид их передаточных характеристик в зависимости от значения параметров T_i приведены в табл. 3.2.

Таблица 3.2

Типовые звенья первого порядка и их передаточные характеристики

Значения параметров	Передаточная функция	Наименование звена
T 1	T 2
			Идеальное элементарное дифференцирующее
			Идеальное элементарное интегрирующее
	T 2		Форсирующее (дифференцирующее)
T 1			Инерционное (интегрирующее)
	T 2		Изодромное
T 1		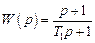	Интегродифференцирующее

3. Звенья второго порядка, описываемые общим дифференциальным уравнением второго порядка следующего вида:

Общее выражение передаточной характеристики звена, описываемого этим дифференциальным уравнением, имеет вид

,

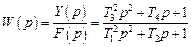где – постоянные времени.

Из всего множества звеньев второго порядка, передаточные функции которых могут быть получены из последнего выражения заданием различных наборов значений постоянных времени, практическое применение находят лишь звенья, у которых . Наименование и выражения таких звеньев и их передаточных характеристик в зависимости от значения параметра 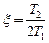приведены в табл. 3.3.

Таблица 3.3

Типовые звенья второго порядка и их передаточные характеристики

Значения параметра ζ	Передаточная функция	Наименование звена
	,	Апериодическое (инерционное)
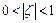
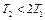
	,	Колебательное
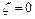
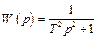	,	Консервативное (резонансное)

Использование рассмотренных выше правил структурных преобразований позволяет рассматривать приведенные в табл. 3.2 выражения как передаточные функции последовательного, параллельного либо встречно-параллельного соединения некоторых элементарных звеньев. В качестве таковых далее будем понимать:

– усилительное (пропорциональное) звено;

– звено чистого запаздывания;

– дифференцирующее звено;

– интегрирующее звено.

Правомерность их выделения в группу элементарных звеньев определяется тем, что выражения их передаточных функций невозможно подвергнуть никаким математическим преобразованиям. Передаточные функции других звеньев всегда можно представить в виде некоторого объединения элементарных звеньев. Так, передаточную функцию форсирующего звена можно представить как

,

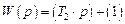т.е. как параллельное соединение объединения, состоящего из двух составляющих:

– последовательного соединения идеальных дифференцирующего (с передаточной функциейи усилительного (с коэффициентом усиления, равным ) звеньев;

– усилительного (с коэффициентом усиления, равным 1) звена.

Структурная схема такого объединения показана на рис. 3.15.

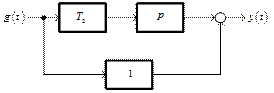
Рис. 3.15. Структурная схема форсирующего звена

Точно так же передаточная функция изодромного звена

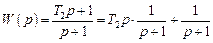
определяет передаточную функцию объединения, состоящего из параллельного соединения двух составляющих:

– последовательного соединения дифференцирующего и апериодического звеньев первого порядка;

– апериодического звена первого порядка и т.д.

Такое представление типовых звеньев через элементарные позволяет определять их характеристики как производные от характеристик элементарных звеньев.

При изучении всех звеньев нас должны интересовать:

1. Определение и математическое описание звена.

2. Передаточная функция.

3. Временные характеристики звена:

− переходная функция;

− импульсная переходная функция.

4. Частотные характеристики:

– в обычном масштабе;

– в логарифмическом масштабе.

5. Примеры.

Содержание этих характеристик было уже рассмотрено в разд. 2. Однако для удобства напомним их содержание непосредственно перед началом анализа типовых звеньев.

Математическое описание строится на основе анализа природы объекта и приводится к некоторому стандартному виду. В нашем случае это будет представление в виде дифференциального уравнения в естественной (во временной области), либо операторной (в пространстве Лапласа) форме.

Для построения передаточной функции достаточно взять отношение выходного сигнала к входному с использованием операторного представления дифференциального уравнения:

.

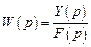Для построения переходной функции можно использовать ее определение: переходная функция есть реакция системы на ступенчатый единичный входной сигнал, т.е.

,

откуда следует, что

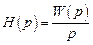, а .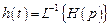

Импульсная переходная (весовая) функция строится аналогично. По определению весовая функция – это реакция системы на входное воздействие в виде δ-функции Дирака (одиночного импульса)

,

откуда следует, что

.

Кроме того, можно воспользоваться определенным ранее отношением между 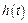и :

.

Частотная передаточная функция получается из передаточной функции заменой .

,

где 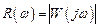– амплитудная частотная характеристика;

– фазовая частотная характеристика;

– вещественная частотная характеристика;

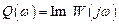– мнимая частотная характеристика.

Логарифмические частотные характеристики (амплитудная и фазовая) строятся на основе соответствующих линейных характеристик.

Общая схема последовательности этапов исследования типовых звеньев представлена на рис. 3.16.

Рис. 3.16. Схема последовательности этапов исследования типовых звеньев

Дата добавления: 2014-01-15