Перелік літератури

План.

Лекція 10.

Тема: Синтез безконтактних та контактних комбінаційних схем у різних базисах.

1. Синтез контактних комбінаційних схем.

2. Синтез безконтактних комбінаційних схем.

3. Синтез схем в базисі І-Ні та АБО-НІ.

При побудові контактної схеми доцільно виявити окремі ділянки, що складаються з однакових контактів, і винести їх у загальні ланцюги, що відповідає винесенню за дужки при алгебраїчних перетвореннях.

За дужки доцільно виносити пряме й інверсне значення змінної, відповідні фронтовому (нормально розімкнутому) і тиловому (нормально замкнутому) контактам. У контактній схемі можливе виділення перемикаючої контактної групи, що дозволяє заощадити число пружин.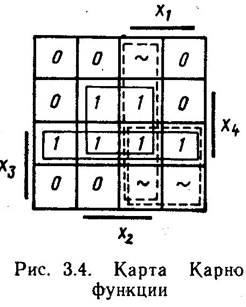

При перетвореннях не повністю певних функцій довизначення доцільно робити з урахуванням можливості винесення максимального числа контактів у загальну частину ланцюга. Найбільш прості рішення для окремих ланцюгів не завжди економічні в цілому для реалізованої ФАЛ.

Для функції, заданою картою Карно (мал. 3.4), мінімальна ДНФ

.

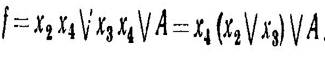Імпликанта А в залежності від способу довизначення й об'єднання кліток може мати чотири різних значення: x_tx₂; x_tx₃; ^₂i₃; x_t (x₂ V x₃). Якби у МДНФ не було члена х₄ (х₂ \/ х₃), варто було б прийняти А = х_гх_г. Однак для одержання більше простої форми доцільно вважати А х_х (х₂ V х_а), тому що в цьому випадку х_г \/ х₃ може бути винесене в загальну частину, тоді / = (х₂ \J х₃)х х(х,в*«).

Якщо прийняти А:= х_хх₂, вийде схема (мал. 3.5, а) з однаковими контактами

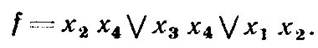
Ця схема може бути спрощена (мал. 3.5, б, в), причому залежно від поєднуваних контактів можуть бути отримані різні схеми:

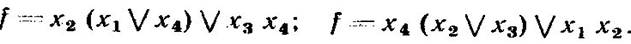У ланцюгах постійного струму введення в схему (див. мал. 3.5, б) діодів збільшує можливості об'єднання окремих ділянок ланцюга й зменшення числа контактів (мал. 3.5, г).

Для спрощення схеми в деяких випадках виявляється доцільним введення у ФАЛ додаткових змінних. Наприклад, формулу ,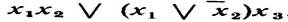

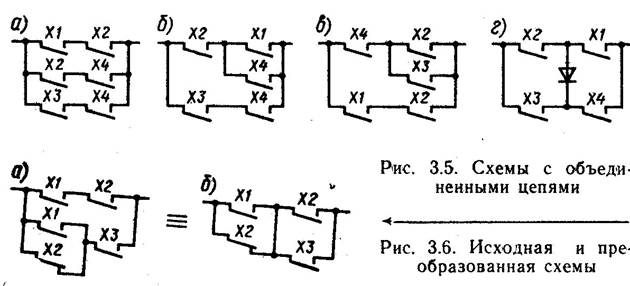
відповідно схемі, наведеної на мал. 3.6, а, доцільно перетворити так

Після перетворень одержимо схему (мал. 3.6, б).

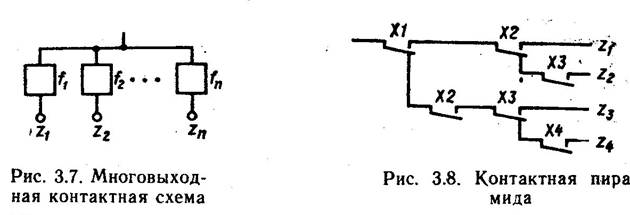
Контактні схеми часто будують у вигляді розгалуженого ланцюга з одним загальним входом і п виходами. Для кожного виходу задають свою ФАЛ: /„ /%,..., /„ (мал. 3.7). У цьому випадку здійснюється спільна мінімізація всіх функцій системи з використанням багатовихідної функції (див. § 2.9). Наприклад, побудуємо схему, що реалізує функції

f₁=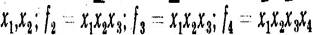Після перетворення багатовихідної функції одержимо

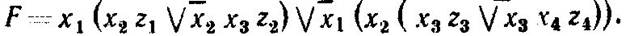На мал. 3.8 наведена схема, що відповідає отриманому вираженню. Вона являє приклад контактної піраміди, у якій вихідний ланцюг замикається тільки в одному із всіх можливих станів пристрою. Контактні піраміди знаходять застосування в шифраторах і дешифраторах інформації систем залізничної автоматики, телемеханіки й зв'язки

Комбінаційний пристрій на елементах І-НІ будують у наступній послідовності: функцію алгебри логіки, що відбиває співвідношення між станами входів і виходів, мінімізують із одержанням МДНФ, потім отримане логічне вираження записують через операцію І -НІ.

Перехід від МДНФ до мінімальної форми в базисі І-НІ (функції Шеффера) здійснюють дворазовим інвертуванням МДНФ і перетворенням по формулі де Моргана. Покажемо це на прикладі.

Карта Карно заданої функції наведена на мал. 3.9. МДНФ функції

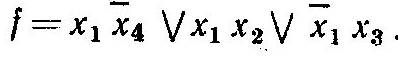
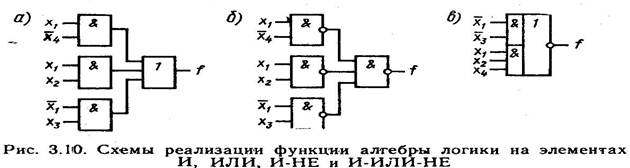
Схема реалізації цієї функції наведена на мал. 3.10, а. Візьмемо подвійну інверсію від правої частини (значення функції не міняється) і застосуємо формулу де Моргана

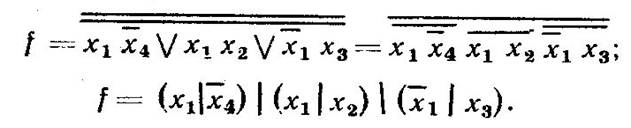Схема реалізації даного вираження наведена на мал. 3.10, б. Отримані схеми (див. мал. 3.10, а, б) аналогічні й відрізняються лише типом логічних елементів. У такий спосіб можна сформулювати наступне загальне правило: при побудові логічної схеми на елементах І-НЕ на основі ФАЛ, представленої в диз'юнктивній нормальній формі (ДНФ), усюди замість елементів И и АБО варто застосовувати елемент І-НЕ.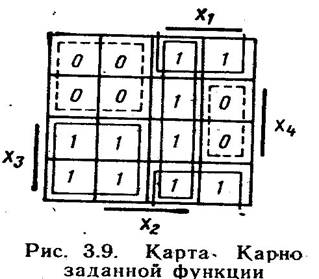

Методика синтезу пристроїв у базисі АБО-НІ аналогічна розглянутій методиці синтезу в базисі І-НІ. Відмінність складається лише в тім, що при мінімізації вихідній ФАЛ повинна бути отримана МКНФ.

Для розглянутої функції (див. мал. 3.9) МКНФ має вигляд

\

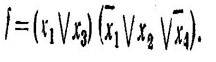
Після перетворення, аналогічного попередній, будемо мати

т. е. отримана функція виражається тільки через операції АБО-НІ. Для реалізації цієї функції потрібно стільки ж логічних елементів АБО-НІ й з тим же числом входів, скільки потрібно елементів І и АБО для реалізації МКНФ в основному функціональному базисі. Отже, при побудові логічної схеми на елементах АБО-НІ на основі ФАЛ, представленої в КНФ> усюди замість елементів І й АБО варто застосовувати елемент АБО - НІ.

Подання в базисі АБО-НІ логічного вираження, заданого в ДНФ, може бути здійснено чотириразовим інвертуванням ДНФ. Наприклад, МДНФ розглянутої функції (див. мал. 3.9) може бути перетворена так

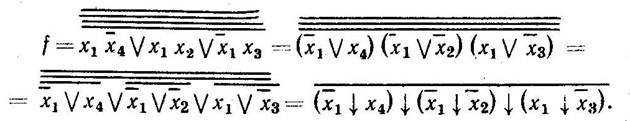
Дане вираження містить тільки операції АБО-НІ.. У деякі системи інтегральних логічних елементів входить елемент І-АБО-НІ. Якщо передбачається його використання, при мінімізації функції доцільно групувати нулі, а не одиниці, і одержувати інверсне значення функцій (на мал. 3.9 це показано штриховими лініями)

.

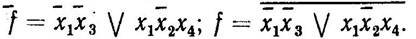Отримане вираження реалізується лише одним елементом (мал. 3.10, в).

Показані вище прийоми побудови схем на елементах І-НІ й АБО-НІ застосовні тільки у випадку необмеженого числа входів цих елементів. У дійсності елементи можуть мати задане число входів (два, три, чотири й т.д.), у зв'язку із чим у логічному вираженні може виявитися кілька членів із числом змінних, перевищуюче число входів елементів. У цьому випадку логічне вираження варто перетворити на основі теореми розкладання (див. §2.11).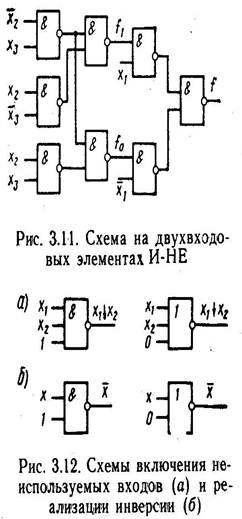

Розглянемо приклад

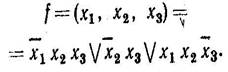
Виконаємо розкладання по змінної х_х:

Схема, що реалізує отриману функцію, наведена на мал. 3.11.

Іноді в схемі використовують елементи із числом входів, що перевищують необхідне. У цьому випадку на невикористовуваний вхід для зменшення впливу перешкод, що наводяться на нього, подають постійний потенціал, що відповідає сигналу логічної 1 для елементів І-НІ й сигналу логічного 0 для елементів АБО-НІ (рис. 3.12, а). Як інвертори застосовують елементи АБО-НІ або І-НІ, у яких використовується лише один вхід, інші входи з'єднують так, як показано на мал. 3.12, б

Основна

1.	Сапожников В.В. и др. Теория дискретных устройств железнодорожной автоматики и телемеханики. М.: 2001.
2.	Сапожников В.В. и др. Дискретные устройства железнодорожной автоматики, телемеханики и связи. -М.: Транспорт, 1988.-256с. Обесп. 1/3.
	Додаткова
2.	Голсуорт В.В. Проектирование цифровых логических устройств.-М.:Машиностроение, 1985.- 226 с. Обесп. 1 екз.
3.	Дискретные устройства автоматизированных систем управления /Под ред. Г.Н.Тимонькина.-Харьков, 1990.-511 с. Обесп.1 екз.
4.	Методичні вказівки Обесп.1/1

Дата добавления: 2014-01-11