
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Умножение матрицы на скаляр, транспонирование матриц, умножение матриц и их основные свойства
|
|
|
|
Определение 1. Пусть A =(aij) – матрица размера m×n над полем P, 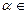 P. Произведением матрицы А на элемент
P. Произведением матрицы А на элемент 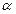 называется матрица С =(сij) размера m×n над полем P, где сij=
называется матрица С =(сij) размера m×n над полем P, где сij= 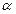 aij, j=
aij, j=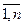 , i=
, i=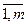 , и обозначается С=
, и обозначается С=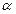 А.
А.
Определение 2. Пусть A =(aij) – матрица размера m×n над полем P, B =(bij) - матрица размера n×k над полем P. Произведением матриц А и В называется матрица С =(сij) размера m×k над полем P, в которой элемент сij равен скалярному произведению i- й строки матрицы А на j -й столбец матрицы B, т.е. сij=AiBj =(ai1 ... ain)⋅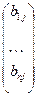 = ai1b1j+…+ainbnj =
= ai1b1j+…+ainbnj =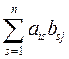 , i=
, i=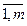 , j=
, j=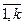 , и обозначается С=A⋅B.
, и обозначается С=A⋅B.
Лемма 1. Пусть А, В, С - матрицы над полем Р. Если существует произведение(АВ) С,то существует и произведение А (ВС),причем (АВ) С=А (ВС).
Доказательство. Пусть существует произведение (АВ) С. Тогда существуют матрицы АВ размера m×n и матрица С размера n×k. Это означает, что существуют матрицы А размера m×l и В размера l×n. Таким образом, существуют матрицы А, В и С соответственно размера m×l, l×n и n×k. Тогда существует произведение BC размера l×k и поэтому существует произведение А (ВС).
Покажем, что (AB) C=A (BC). Пусть (АВ) С= (xij), А (ВС) = (yij), i=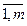 , j=
, j=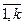 . Покажем, что xij=yij, i=
. Покажем, что xij=yij, i=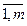 , j=
, j=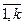 . Пусть A =(aip), B =(bps), С =(сsj), АВ=R= (ris), BC=T= (tpj), s=
. Пусть A =(aip), B =(bps), С =(сsj), АВ=R= (ris), BC=T= (tpj), s=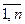 , p=
, p=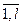 . Тогда
. Тогда
xij=RiCj= 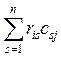 =
=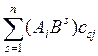 =
=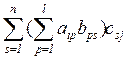 =
=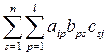 ,
,
yij=AiTj =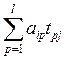 =
=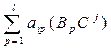 =
=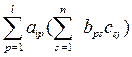 =
=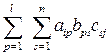 .
.
Таким образом, xij=yij, i=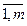 , j=
, j=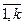 . Следовательно, (AB) C=A (BC). Лемма доказана.
. Следовательно, (AB) C=A (BC). Лемма доказана.
Лемма 2. Пусть A, B, C – матрицы над полем P следующих размеров: А и В – размера m×n, С – размера n×k. Тогда(А+В) С=АС+ВС.
Доказательство. Пусть (А+В) С= (xij), АС+ВС= (yij), i=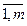 , j=
, j=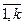 . Покажем, что xij=yij, i=
. Покажем, что xij=yij, i=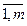 , j=
, j=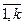 . Пусть A =(ais), B =(bis), С =(сsj), i=
. Пусть A =(ais), B =(bis), С =(сsj), i=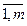 , s=
, s=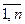 , j=
, j=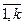 . Тогда
. Тогда
xij= (A+B) iСj= 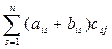 =
=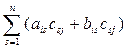 =
=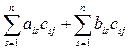 = AiCj+BiCj = yij.
= AiCj+BiCj = yij.
Следовательно, (А+В) С=АС+ВС. Лемма доказана.
Определение 3. Пусть A - матрица размера m×n над полем P. Транспонированием матрицы А называется операция замены в матрице А i -й строки на i -й столбец, i= 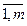 . Матрица, полученная в результате транспонирования матрицы A, называется матрицей, транспонированной к матрице A, и обозначается tA.
. Матрица, полученная в результате транспонирования матрицы A, называется матрицей, транспонированной к матрице A, и обозначается tA.
Пример 1. Если A =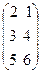 , то tА =
, то tА =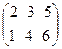 . Таким образом, если А – матрица размера m×n, то tА - матрица размера n×m.
. Таким образом, если А – матрица размера m×n, то tА - матрица размера n×m.
Лемма 3. Если произведение AB существует, то существует произведение tB tA, причем t (AB) = tB tA.
Лемма 4. Если А – матрица размера m × n над полем Р, то АЕn=EnA=A.
Доказательство осуществляется непосредственной проверкой.
Через Mn(P) обозначается множество всех квадратных матриц n -го порядка над полем P.
Замечание. Из свойств операций над матрицами следует, что Mn(P) - ассоциативное кольцо с единицей. Отметим, что умножение матриц некоммутативно (см. примеры на практических занятиях).
Лемма 5. Пусть А и В – матрицы над полем P, 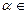 P. Тогда
P. Тогда 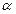 AB= (
AB= (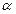 A) B=A (
A) B=A (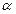 B).
B).
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 433; Нарушение авторских прав?; Мы поможем в написании вашей работы!