Пример 2.10.1

Тема 2.10. Методы решения задач нелинейного программирования.

Исследовать на экстремум функцию

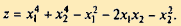
Решение. Находим частные производные:

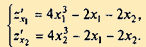
(2.30)

Приравниваем частные производные нулю:

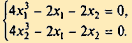
(2.31)

Решаем систему уравнений (2.31). Вычитая из первого уравнения второе, получим 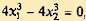, поэтому x₁ = x₂, и из первого уравнения найдем 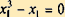, откуда x₁ = 0 или x₁ = ±1.

Имеем три стационарные точки: X¹ = (0; 0); X² = (1; 1); X³ = (-1; 1).

Найдем вторые частные производные, используя (2.30):

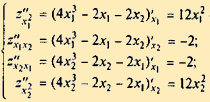
Вычисляем значения вторых частных производных в каждой стационарной точке, составляем определитель Δ и применяем достаточные условия экстремума.
В точке X¹ = (0; 0) a₁₁ = - 2; a₁₂ = a₂₁ = - 2; a₂₂ = - 2;

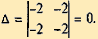
Вопрос об экстремуме остается открытым (такая точка называется седловой). В точке X² = (1; 1) (а также и в точке X³ = (-1; 1)):

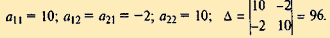
Функция в этих точках имеет минимум, так как Δ > 0, a₁₁ > 0.

Z _min = -2 ¹

Выше шла речь о локальном экстремуме функции n переменных. Как правило, в практических задачах необходимо определить наибольшее и наименьшее значения функции (глобальный экстремум) в некоторой области. Говорят, что функция z = f (X) имеет в точке X⁰ заданной области D глобальный максимум (наибольшее значение) или глобальный минимум (наименьшее значение), если неравенство f(X) ≤ f(X⁰) или соответственно выполняется для любой точки X € D.
Если область D замкнута и ограничена, то дифференцируемая функция z = f (X) достигает в этой области своих наибольшего и наименьшего значений или в стационарной точке, или в граничной точке области (теорема Вейерштрасса).

Граница области D аналитически может быть задана системой уравнений (условий) относительно переменных x₁, x₂,..., x_n. Поэтому, исследуя экстремальные свойства функции на границе, необходимо решить задачу определения условного экстремума.

Условный экстремум. Пусть необходимо найти экстремум функции z = f (x₁, x₂,..., x_n) при условии, что переменные x₁, x₂,..., x_n удовлетворяют, уравнениям

φi (x1, x2,..., xn) = 0, i = 1, 2,..., m, m < n

(2.32)

Предполагается, что функции f и φ_i , имеют непрерывные частные производные по всем переменным. Уравнения (2.32) называют уравнениями связи. Говорят, что в точке удовлетворяющей уравнениям связи (2.32), функция z = f (X) имеет условный максимум (минимум), если неравенство f(X⁰) ≥ f(X)(f(X⁰) ≤ f(X)) имеет место для всех точек X, координаты которых удовлетворяют уравнениям связи.
Легко заметить, что задача определения условного экстремума совпадает с задачей нелинейного программирования.
Один из способов определения условного экстремума применяется в том случае, если из уравнений связи (2.32) m переменных, например x₁, x₂,..., x_n, можно явно выразить через оставшиеся n - m переменных:

xi = ψi (xm + 1 ,..., xn), i = 1, 2,..., m,

(2.33)

Подставив полученные выражения для x_f в функцию z, получи
м z_i = f(ψ_i (x_{m + 1} ,..., x_n),..., ψ_m (x_{m + 1} ,..., x_n), x_{m + 1} ,..., x_n)

или

z = F(xm + 1 ,..., xn)

(2.34)

Задача сведена к нахождению локального (глобального) экстремума для функции (2.34) от n - m переменных. Если в точке 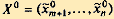функция (2.34) имеет экстремум, то в точке 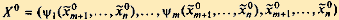функция z = f (x₁,..., x_n) имеет условный экстремум.

Дата добавления: 2014-01-15