Криптографическая модель

В этой модели попытались использовать понятие вычислимой различимости.

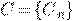- множество концепций

- множество гипотез

А – алгоритм распознавания, выполняемый за полиномиальное время.

Различия моделей (со слайда):

· Наличие множества сигналов, которые следует обнаруживать в теории обнаружения вторжений по сравнению с единственным сигналом в типичной теории обнаружения сигналов.

· Природа наблюдаемых событий – дискретная в теории обнаружения вторжений и непрерывная в теории обнаружения сигналов.

Выводы (со слайда):

· Знание распределений нормального поведения и поведения, относящегося к вторжению, значительно повысит качество работы СОВ;

· Получение распределений нормального поведения и поведения, относящегося к вторжению, является нетривиальной задачей;

· Существенное различие проблемной области.

Вопрос 6. Задача распознавания образов

Задача распознавания образов:

· сопоставление двух образцов для отнесения их к одному классу

· сопоставление данных о поведении системы с набором поведения системы

Есть наборы данных и надо построить решающую функцию, которая показывала бы, к какому набору данных относится наша решающая функция.

Задача классификации

Объект исследования - множество объектов

Дано - обучающая выборка

Требуется построить алгоритм классификации

y(S) - основной признак (опасное или безопасное поведение)

-тренировочная выборка

где L - минимальная функция ошибок

Можно вводить штрафные вещи для избежание переобучения.

Введем описание предметной области

Представление класса:

· Перечисление членов класса

· Общность свойств(описание)

· кластеризация (один из способов обучения без учителя)

На сегодняшний день нет ничего на самом деле:

· Мат теория СОВ не создана

· Нет теории для обоснования выбора

Если существует две группы, например, нормальное поведение и аномальное поведение, которые распределены прямой на две полуплоскости. Если в процессе классификации получили уравнение такой прямой и получили новые значения – то сможем классифицировать.

Проблема заключается в том, что надо оценить коэффициенты и вряд ли получится построить прямую – будет кривая – будет нелинейная функция. Пространство окажется не двумерным.

От решающей функции переходим и получаем решающую функцию для n-мерного пространства.

Второй момент может оказаться, что одной кривой не ограничить. Переходим из x в f(x).

Возникает проблема – специфичность.

В задачу распознавания образа вводится два компонента – то, на сколько точно мы классифицируем и штраф за использование функции. Получается слишком специфичная система или проблема переобучения – результат не использования этих методов. Когда система не распознает никакие данные кроме тех, на которых она была обучена.

Существует теорема о том, что любые два различных образа в пространстве могут быть разделены.

Следующий момент, который есть – про нелинейность. Вводят понятие ядра. Его вводят, чтобы можно было рассматривать многомерные пространства признаков. Если известно что-то о природе данных, которое обрабатываем, то будет плохо иметь Евклидово пространство. Ядро – функция, вычисляющая произведение точек в пространстве признаков.

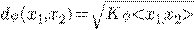
Обоснованный систематизированный выбор. Возможен выбор алгоритмов распознавания образов для конкретной задачи обнаружения вторжений. То есть большой математический аппарат, из которого можно выбрать.

Существует обобщенная теория обучения. Говорит следующее. Есть некоторый обобщенный алгоритм. Теория говорит, что не существует единственного предпочтительного алгоритма распознавания образов в общем случае. То есть все зависит от предметной области. Зато эта теория дает полезные оценки, например, для задач особого вида, количество образцов, с помощью которых надо обучать систему для адекватного покрытия пространства задачи. В частном случае для булевых функций, нейросетей и некоторых других видов.

В общем случае, задача обучения ставится следующим образом: есть множество прецедентов и множество откликов, этот набор называется обучающим множеством. На основе этого множества надо построить алгоритм, который сможет распознавать образы. Для оценки качества вводится функционал для контроля. Обычно имеющееся множество делится на 2 части - 80% для обучения и 20% для оценки ошибки.

Иногда может оказаться то, что лучше пропустить одну точку на обучении и нарисовать разделяющую прямую между плохим и хорошим множеством, чем нарисовать хитрую кривую. Это проблема переобучения.

Обучение без учителя изучает класс задач, в которых надо существование независимости от учителя. Например, класс задач кластерного анализа. Ест только описание объектов, с которыми надо работать. Кластерный анализ – разбиение данной выборки на по возможности не пересекающиеся множества – кластеры. Объекты разных кластеров должны существенно различаться.

Есть два момента – адекватно обучить с учителем или без, а затем задача классификации.

Существует несколько видов распознавания образов – эвристический (так сказал эксперт), статистические (методы, использующие статистики, выявление аномалий и тд), лингвистические (формальные грамматики и тд.). Для формальных грамматик: из пакетов формируют сигнатуры, из сигнатур – слова, из слов – атаки.

Распознавание сигнатур – эвристический метод, и другие методы.

Математический аппарат:

· Эвристические методы;

· Математические методы

· Лингвистические методы

Эвристические методы:

· За основу эвристического подхода взяты интуиция и опыт человека;

· Используются принципы перечисления членов класса и общности свойств.

Математические методы:

· Правила классификации формулируются и выводятся в рамках определенного математического формализма с помощью принципов общности свойств;

· Математические методы распознавания можно разделить на 2 класса:

o Детерминистские

o Статистические

Лингвистические методы:

· Описание образов производится с помощью непроизводных элементов (подобразов) и их отношений;

· Образ можно описать с помощью иерархической структуры подобразов, аналогичной синтаксической структуре языка.

Природа входных данных:

· Определяется набором образцов данных (состоят из атрибутов);

· Природа атрибутов влияет на используемую технику выявлений аномалий

· Статистические техники используются для непрерывных и категориальных данных;

· Техники поиска ближайших соседей используют метрики расстояний, основанные на типах атрибутов.

Представление класса:

· Класс характеризуется перечнем входящих в него членов;

· Класс характеризуется некоторыми общими свойствами, присущими всем его членам;

· При рассмотрении класса обнаруживается тенденция к образованию кластеров в пространстве образов.

Принципы построения систем распознавания образов:

· Принцип перечисления членов класса

· Принцип общности свойств

· Принцип кластеризации

Дата добавления: 2014-01-15